FDA

Tutorials

Provide the expressions for the basis functions for a length 7 Fourier basis with period ω.

Let ω = 2π/P where P is the period. Constant ω defines the period of oscillation of the first sine/cosine pair and thus the first 7 Fourier functions are given as: Φ(t) = (1,sin(ωt), cos(ωt),sin(2ωt), cos(2ωt), sin(3ωt), cos(3ωt)),

How would you express a functional object x(t) based on the length 7 Fourier basis function in part(a) and the coefficients c0, c1, . . . , c6.

x(t) = c0 + c1 sin(ωt) + c2 cos(ωt) + c3 sin(2ωt) + c4 cos(2ωt) + c5 sin(3ωt) + c6 cos(3ωt)

Calculate the first derivative of x(t)in part (b) with respect to t and show that it has the same period as x(t).

How many basis functions do we use when we are using order 4 B-splines with 27 knots (i.e. 25 interior knots)

Number of basis functions: order + number interior knots = 4 + 25 = 29.

Suppose we are interested in estimating the third derivative of a function. What should be the minimum order of B-splines to achieve this goal.

The order of the spline should be at least 3 + 2 = 5 if we are interested in 3 derivatives of a function.

In each case (a) and (b) state the maximum number of adjacent intervals the B-splines have positive support over

4 and 5

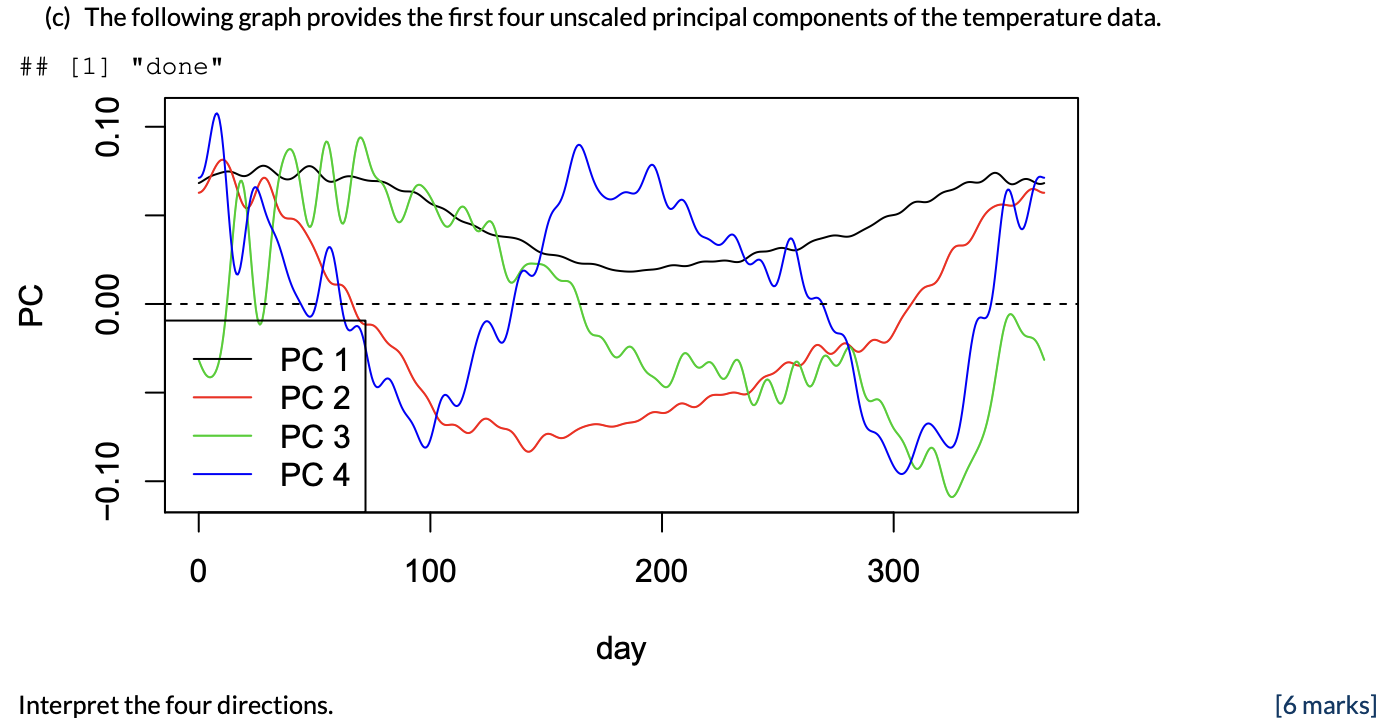
How can you use the harmonic acceleration given in part(b) to penalize a curve for its departure from periodicity

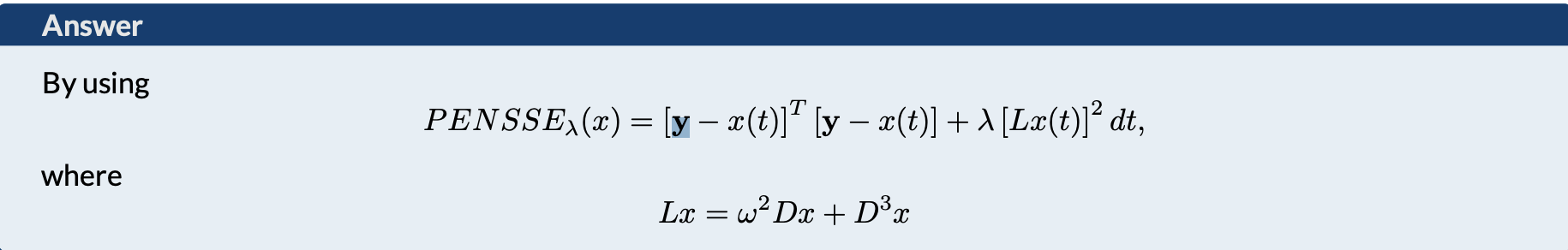
Four as the rest of the variances are very close to zero. Three is also a correct answer

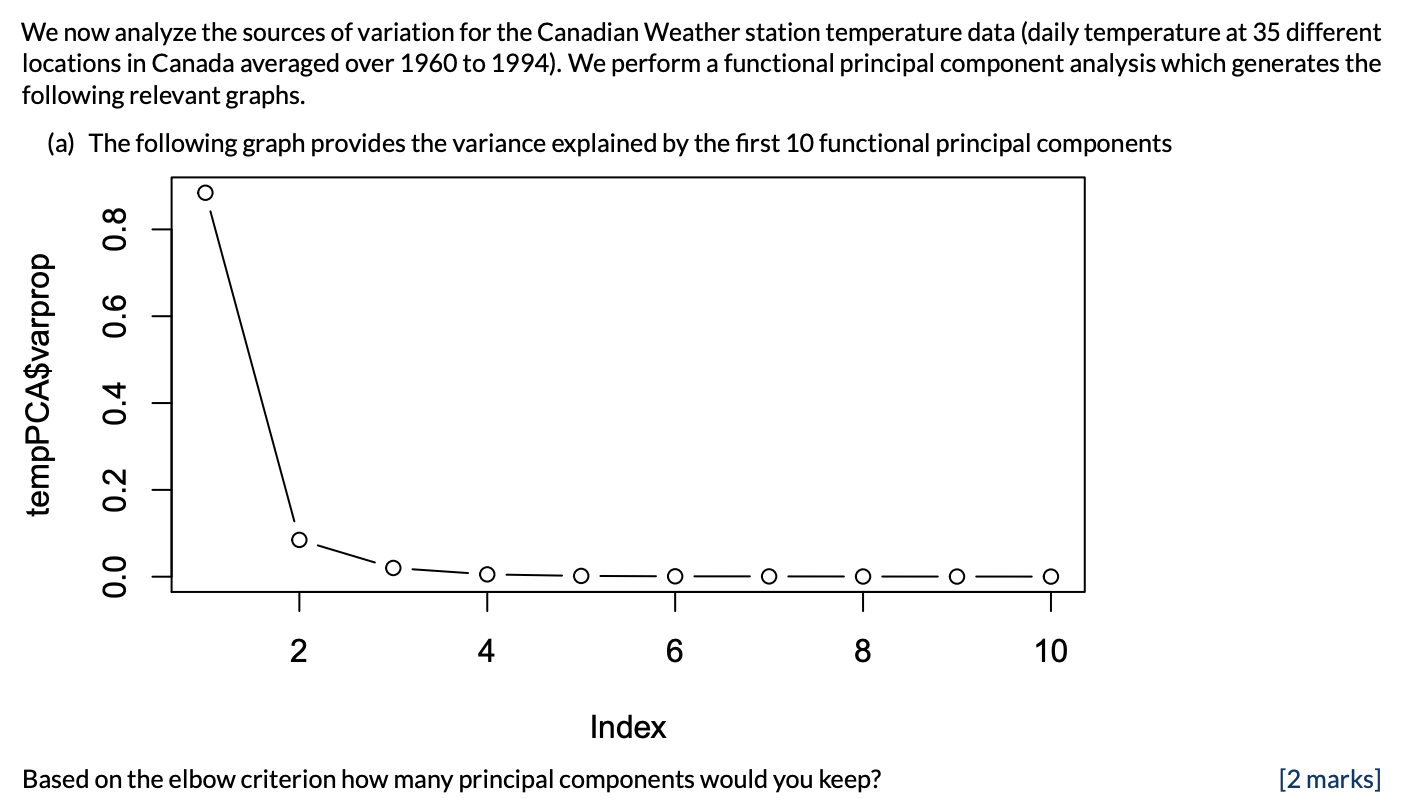
4 components

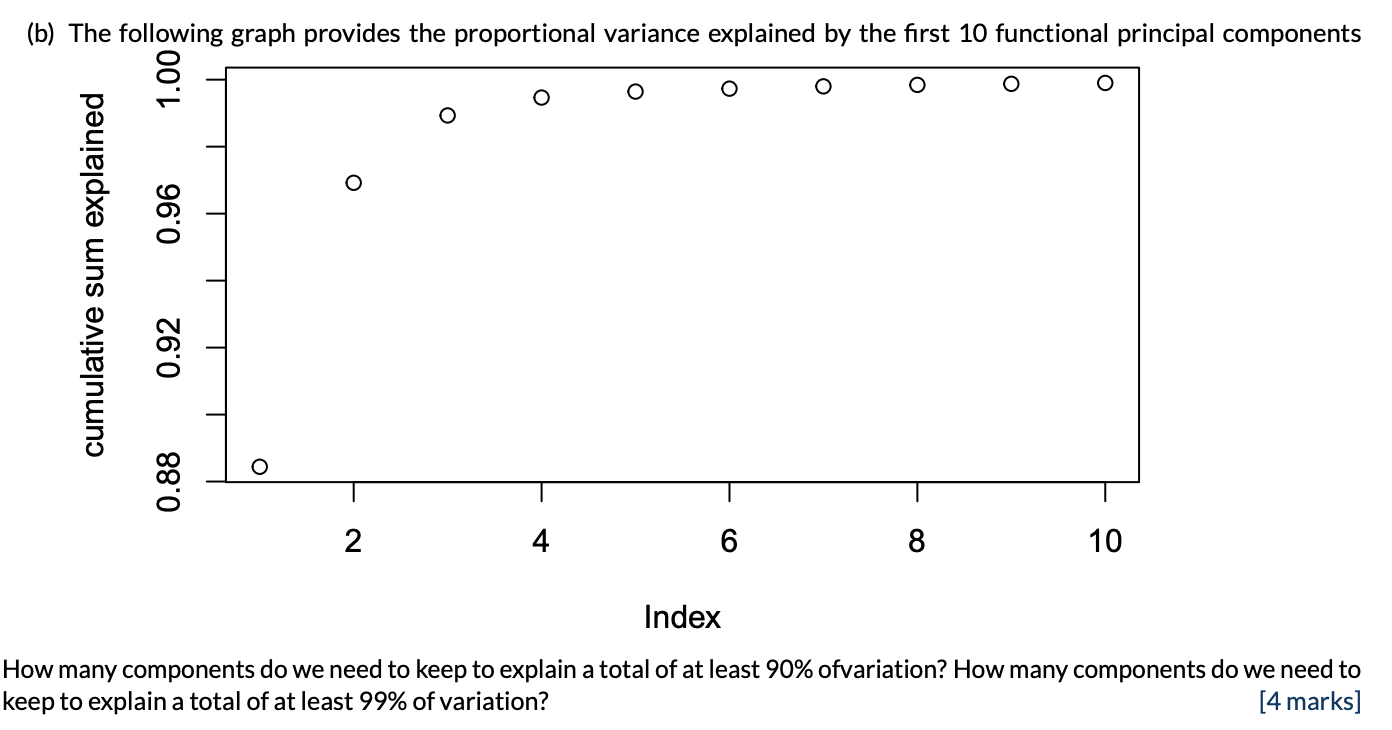
THE PC’s

- PC1 – over-all temperature

- PC2 – relative temperature of winter and summer

- PC3 – contrast between fall and spring

- PC4 – relative lengths of summer/winter

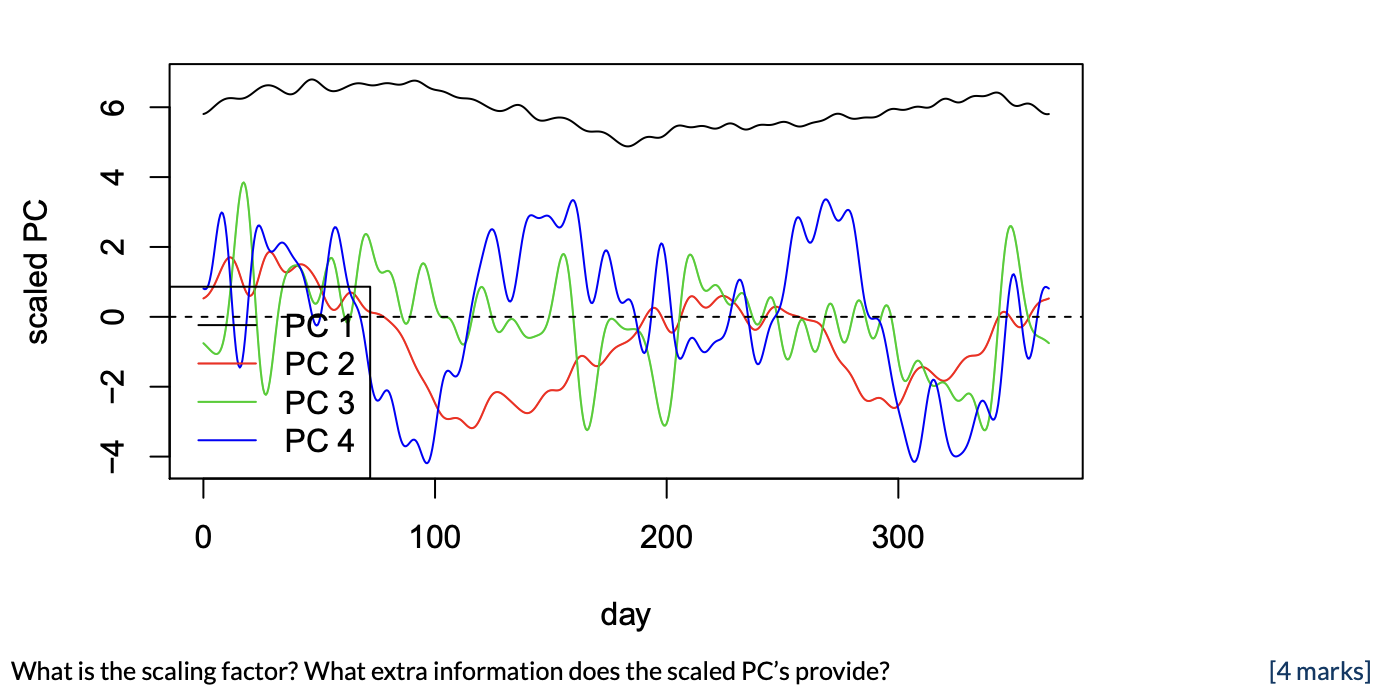
The PC’s are scaled by the amount of variation they explain Provides a better interpretation of the relative importance of the different directions in PC1, PC2, . . . , PC4.

Suppose we have a multivariate function

x(t) = (x1(t), x2(t), x3(t))

(a) Propose a symmetric-bilinear inner-product for x(t)for performing multivariate FPCA.

(b) Show that your inner-product is symmetric and bilinear.

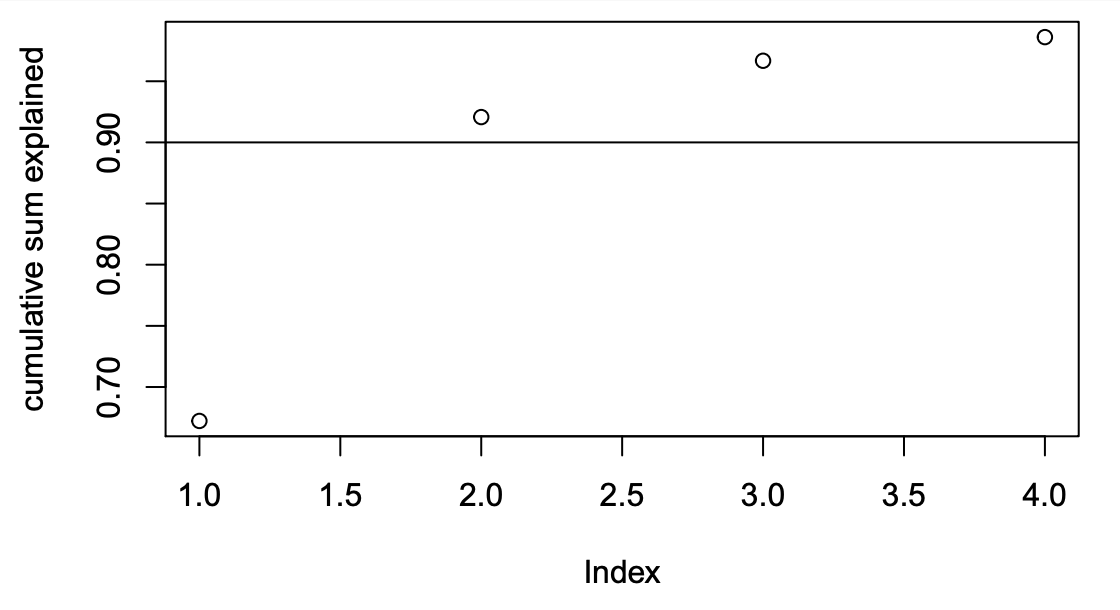
Need 2 components

Are smoothed functional principal components orthogonal to each other?

No

Define a square integrable function