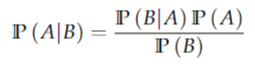P1. Probability

Sample Space.

The set Ω. It contains all possible outcomes that we are considering.

Event

A subset of Ω (including Ω itself)

Event space

A set of subsets of Ω which must satisfy certain properties. The event space defines the set of all describable events to which we want to assign probabilities

Probability

A function P that assigns, for all events in F:
P(A) >= 0 for all A in F
P(Ω) = 1
If A1, A2, … in F are mutually exclusive, then P(A1 U A2 U…) = P(A1) + P(A2) + …

The complement rule

The probability that an event occurs is always equal to 1 minus the probability that the event does not occur

The Probability of the Union of Two Events Rule

The probability of A or B is:

P(A ∪ B) = P(A) + P(B) − P(A ∩ B)

Bounds on Probabilities Rule

The probability of A or B is weakly less than the

sum of their probabilities:

P(A ∪ B) ≤ P(A) + P(B)

Logical consequence rule

If B logically entails A then P(A) ≥ P(B)

Kolmogorov definition of a conditional probability

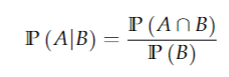
Law of total probability

This says that given a partition {B1, B2} of Ω then for any event A:
P (A) = P (A ∩ B1) + P (A ∩ B2)
P (A) = P (A|B1) P (B1) + P (A|B2) P (B2)

Two events A and B are independent if (intersect)

P (A ∩ B) = P(A)P (B)

Two events A and B are independent if (conditional)

P(A|B) = P(A)

Bayes’ Rule