Integrals & Derivatives Rules [In Chain Rule Form] Review
1/28
Earn XP
Description and Tags
Calculus 1 & 2 Review
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No study sessions yet.
29 Terms
![<p>Power Rule [Derivative]</p>](https://knowt-user-attachments.s3.amazonaws.com/3594d395-44a7-4cae-91be-78b123c6d61c.png)
Power Rule [Derivative]
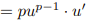
![<p>Exponential Rule [Derivative]</p>](https://knowt-user-attachments.s3.amazonaws.com/5c3c7a23-08e8-4135-9920-e401196c0e25.png)
Exponential Rule [Derivative]
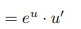
![<p>Generalized Exponential Rule [Derivative]</p>](https://knowt-user-attachments.s3.amazonaws.com/14cb74a5-9fd5-4795-9c94-7b6ebf0651ec.png)
Generalized Exponential Rule [Derivative]
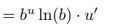
![<p>Logarithm Rule [Derivative]</p>](https://knowt-user-attachments.s3.amazonaws.com/065c65cb-e1a1-428d-bbf0-adcfeaa58a89.png)
Logarithm Rule [Derivative]
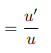
![<p>Product Rule [Derivative]</p>](https://knowt-user-attachments.s3.amazonaws.com/3ecc69cd-9bbf-41bf-9531-d673636ad9c7.png)
Product Rule [Derivative]
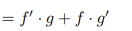
![<p>Quotient Rule [Derivative]</p>](https://knowt-user-attachments.s3.amazonaws.com/fdf6e80f-d729-4fe3-bc8e-6f30d4ccc4b9.png)
Quotient Rule [Derivative]
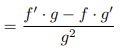
![<p>Power Rule [Integral]</p>](https://knowt-user-attachments.s3.amazonaws.com/441c005e-d4a9-40ed-ae8f-722e531ec28b.png)
Power Rule [Integral]
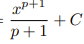
![<p>Exponential Rule [Integral]</p>](https://knowt-user-attachments.s3.amazonaws.com/4fc2a88a-adb5-4c31-afe4-b0965de2df0b.png)
Exponential Rule [Integral]
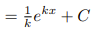
![<p>Generalized Exponential Rule [Integral]</p>](https://knowt-user-attachments.s3.amazonaws.com/a8ee727a-7933-43b7-855c-e4e0342006a1.png)
Generalized Exponential Rule [Integral]
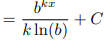
![<p>1/x Rule [Integral]</p>](https://knowt-user-attachments.s3.amazonaws.com/fa603dfc-e9d9-444d-8cf1-293a3c93fba2.png)
1/x Rule [Integral]
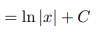
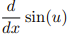
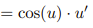
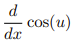
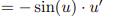
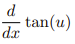
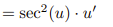
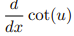
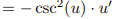
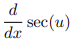
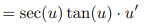
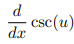
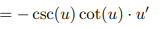
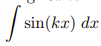
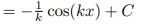
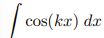
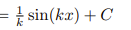
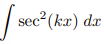
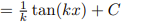
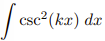
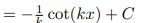
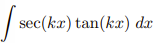
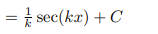
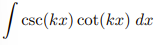
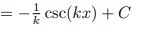
![<p>Inverse Trig [Derivative]</p>](https://knowt-user-attachments.s3.amazonaws.com/c8857b35-e7d9-43fc-a21d-28a1cbc62119.png)
Inverse Trig [Derivative]
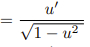
![<p>Inverse Trig [Derivative]</p>](https://knowt-user-attachments.s3.amazonaws.com/91bc2836-be91-4b4d-93c8-ecb1c3192d22.png)
Inverse Trig [Derivative]

![<p>Inverse Trig [Integral]</p>](https://knowt-user-attachments.s3.amazonaws.com/f9aa59a2-cfa4-4365-b5fb-340c17b0eb93.png)
Inverse Trig [Integral]
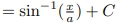
![<p>Inverse Trig [Integral]</p>](https://knowt-user-attachments.s3.amazonaws.com/0b1ac738-b728-4452-af51-4e36061afba9.png)
Inverse Trig [Integral]
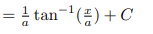
U-Substitution

Integration By Parts
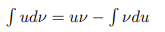
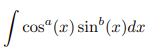
How do I solve this form?
If one exponent is odd, then use the Pythagorean Identity to set up a u-substitution. cos^2x + sin^2x = 1.
or
If both exponents are even, then use half-angle identities multiple times until all powers of the trig functions vanish to integrate. cos^2(x) = 1/2 + 1/2 cos(2x) sin^2(x) = 1/2 − 1/2 cos(2x)