Data analysis midterm 1

Correlational designs

Measures two variables as a naturally occurred to see if there’s a relationship

Operational definition

Describes how your variable is measured and what it means

Experimental method

Manipulating one variable while controlling the other variable to see if there’s a relationship

Independent variable

Predictor variable, variable that’s being manipulated in an experiment eg. Sitting with a friend versus sitting with a stranger.

Dependent variable

The outcome variable, the variable that’s being measured as the outcome eg. Roller coaster enjoyment.

Systematic variation

Difference in outcome created by a specific experimental manipulation (eg. Sitting with a stranger versus sitting with a friend.)

Unsystematic variation

Variation that’s not due to the effect we’re interested in (eg. Natural differences, time of day, etc..) things that may affect ride enjoyment that are not a part of the experiment

Within subject

The same entities take part in all experimental conditions

Problem for within subject, design, designs, and the solution

Practice effects, familiarity and boredom

Solution can be counter balancing: some will start with a different condition and then go to the stranger condition, vice versa

Between subject designs

Having different entities in experimental conditions

Types of variables

Discrete and continuous

Discrete variables

Finite numbers (whole number) eg. Age

Continuous variables

Numbers that have infinite number of possible values (fractions, decimals, time, weight, grades)

Scales of measurement

Nominal, ordinal, interval, and ratio

Nominal

Data that can be separated into exclusive categories (eg. Jobs (teacher, lawyer doctor.) relationship status (married single divorce)

Ordinal

Assigning numerical values to categories in an order sequence (eg. Gold,Silver,Bronze in a race = 1,2,3

Interval and ratio

Assigning numerical values in an order sequence (eg.timed races)

Interval

Zero is arbitrary, doesn’t include a true zero (eg.temperature, 0° doesn’t mean no more temperature)

Ratio

Zero is as meaningful as absolute zero (eg. Gas tank with zero gas means gas is absent.)

Measurement error

The difference between what we know is true and what we measure. In this image, the measurement error would be 3 pounds because the absolute truth was 100 pounds and the cheap bathroom scale was 103 so we would just subtract the two measurements

Validity

Is it measuring what needs to be measured?

Reliability

Weather an instrument can be interpreted consistently across situations

Central tendencies

Mean, median, and mode

Mode

The most frequent scores

Bimodal

Having 2 modes

Multimodal

Having several modes

Median

The middle score when scores are ordered

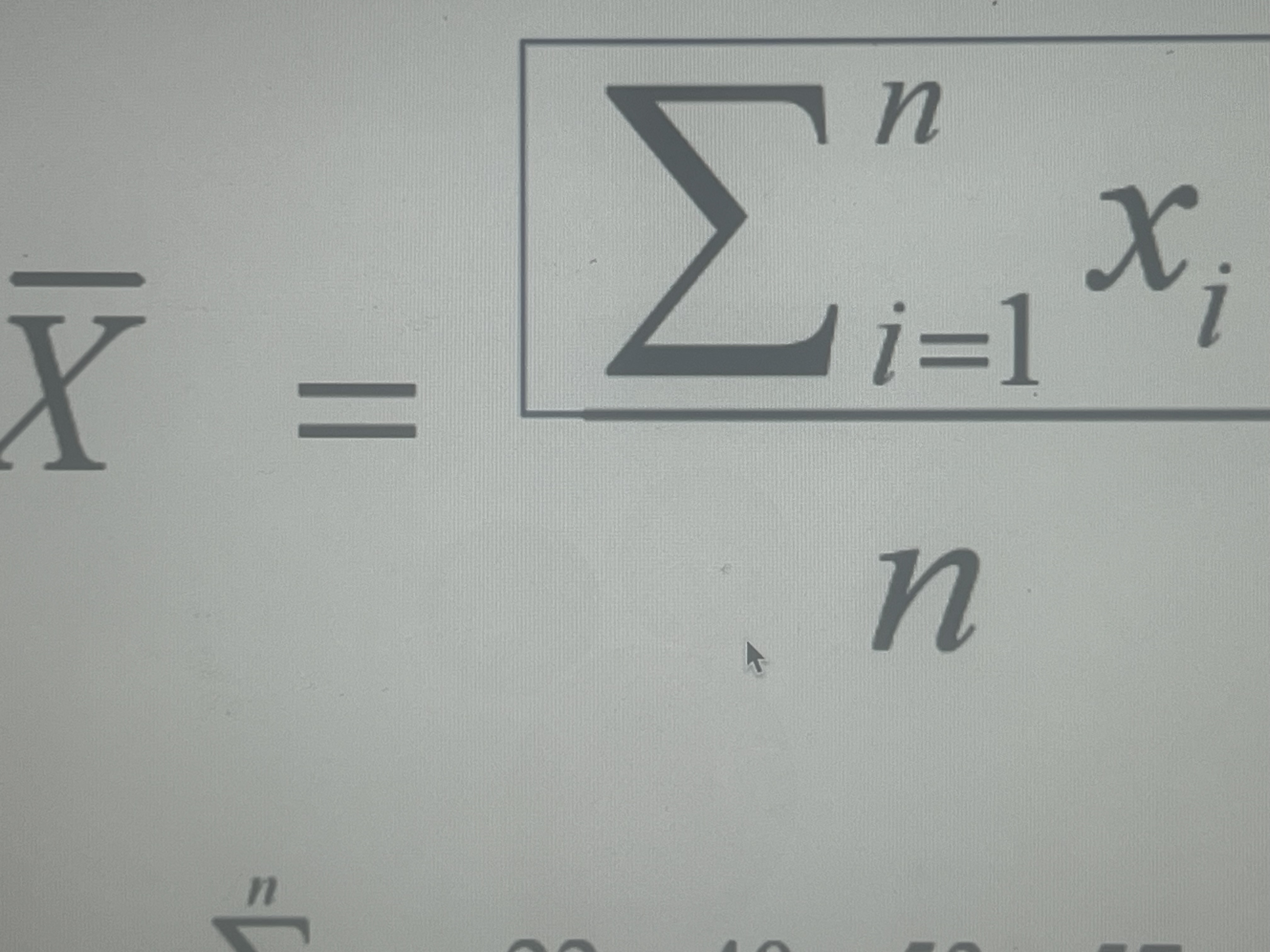
Sum of score is divided by the number of scores

Mean equation

frequency distribution

Organize data by the number of individuals located within each category

N = 10

N= the amount of people in the study

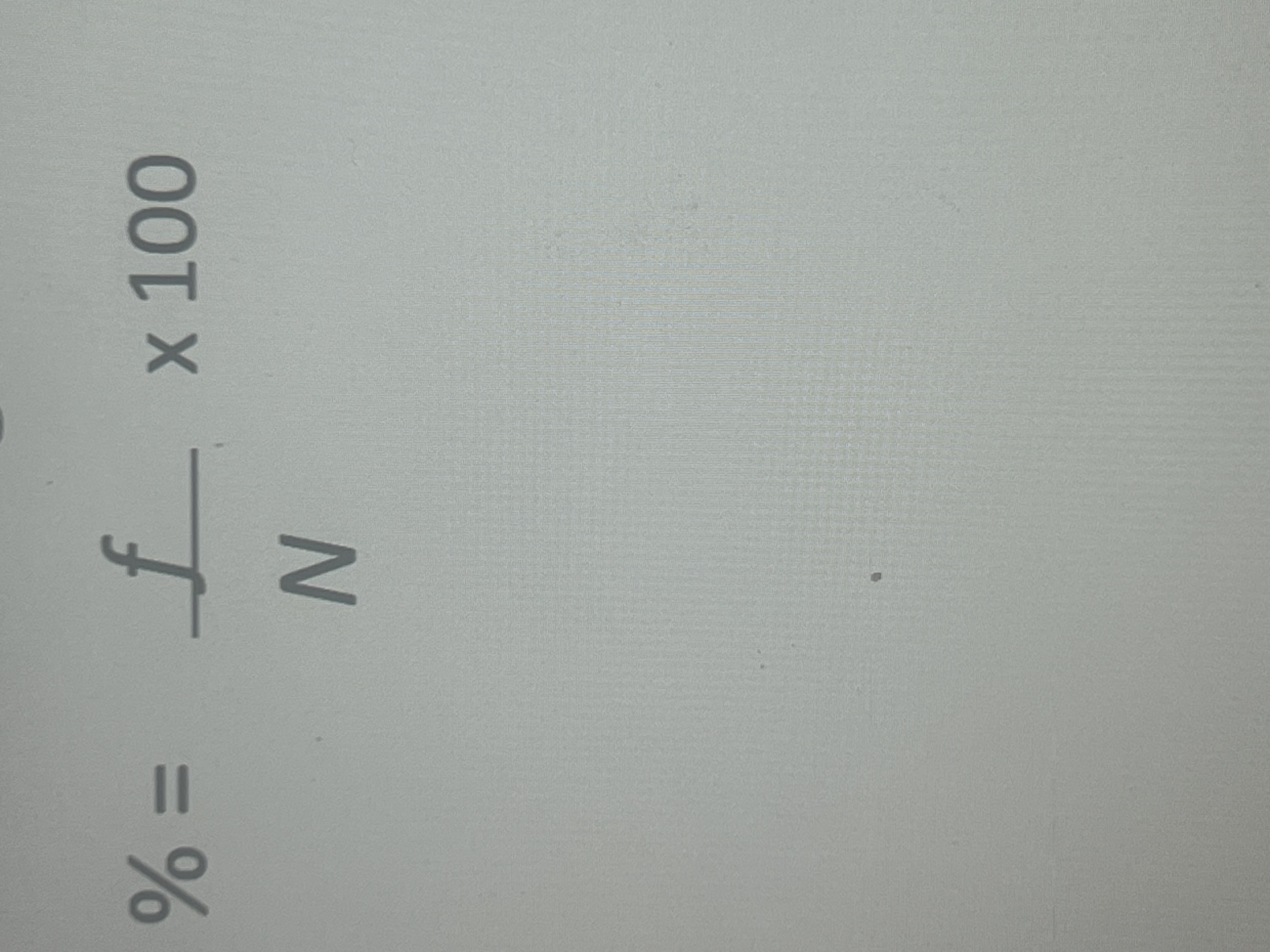
%= f (frequency) divided by n (number of participants x 100

Percentages equation

Percentile ranks

The percent of people what score is equal to or less than a specific value (if I scored in the 70th percentile 70% of people score lower than me

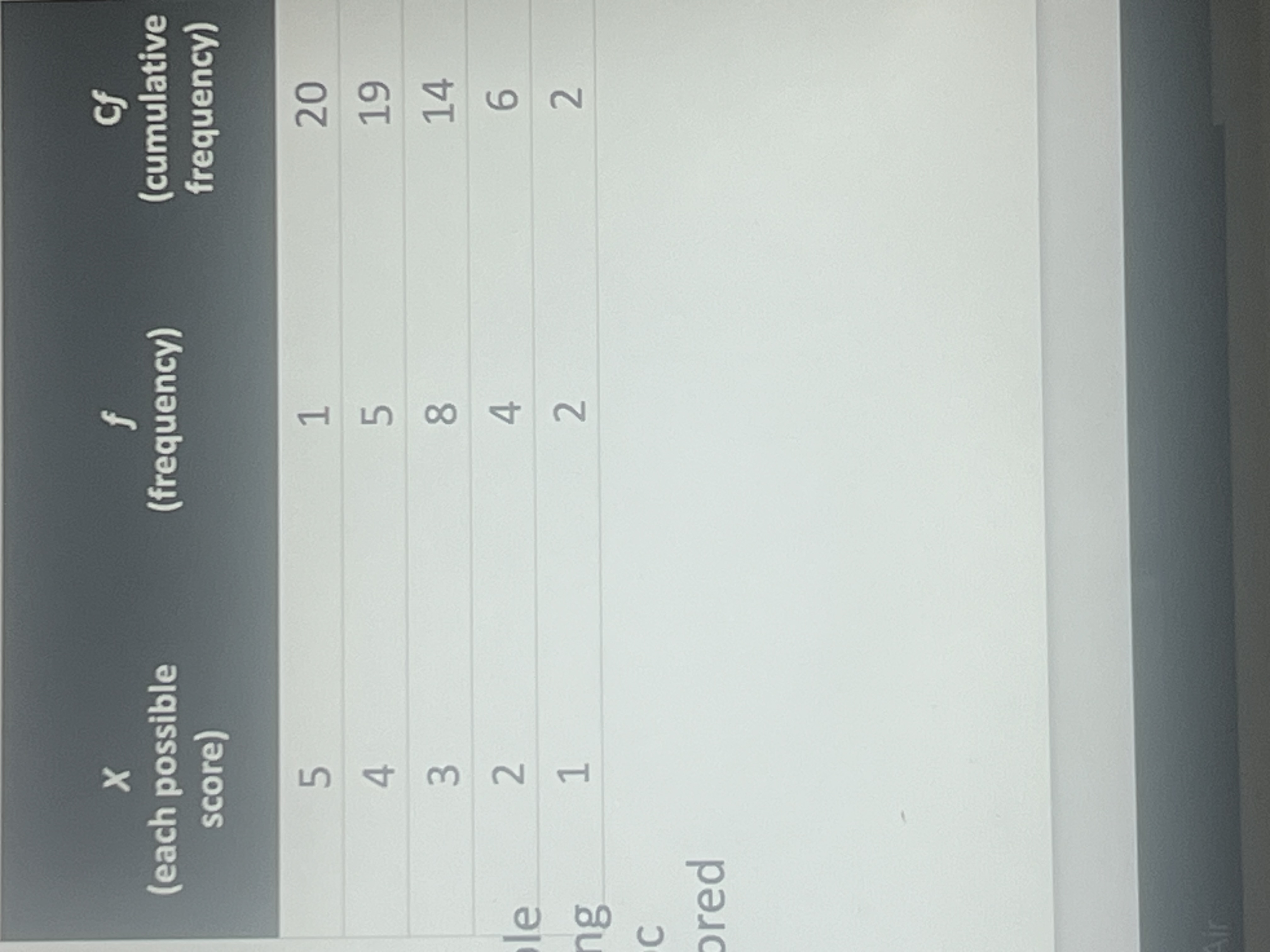
Cumulative frequency

The amount of people at or below a square

Cumulative percentage equation (percentage rank)

C%= cf (cumulative frequency) divided by n x 100

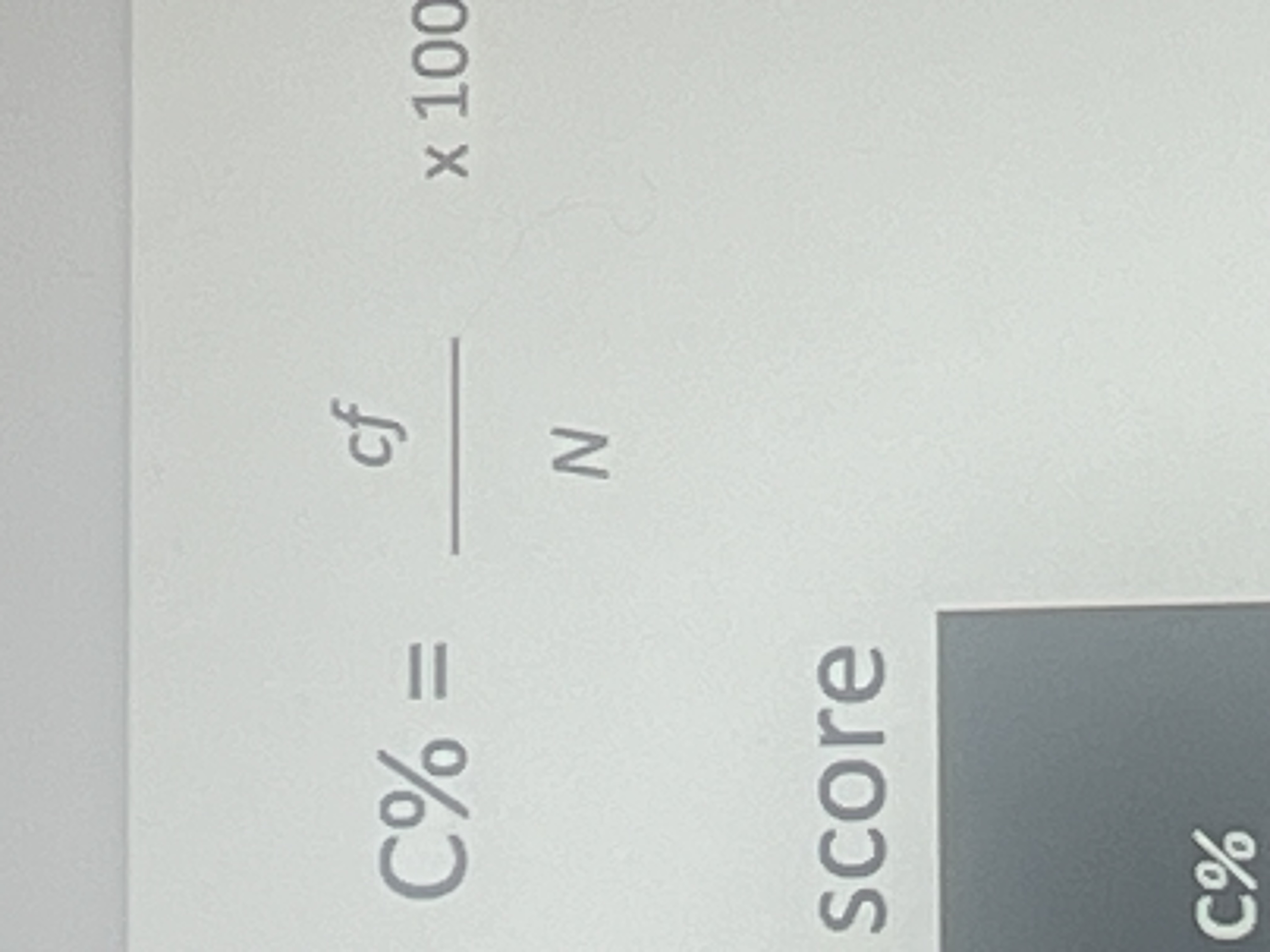
Symmetrical distribution

If it’s perfectly symmetrical, it means the main median and mode are the same

Positive skew

Negative skew

Skew

The symmetry of the distribution

Kurtosis

The heaviness of the tails

Leptokurtic

Heavy tails (pointy) higher probability of extreme values

Platykurtic

Light tails (flatter)

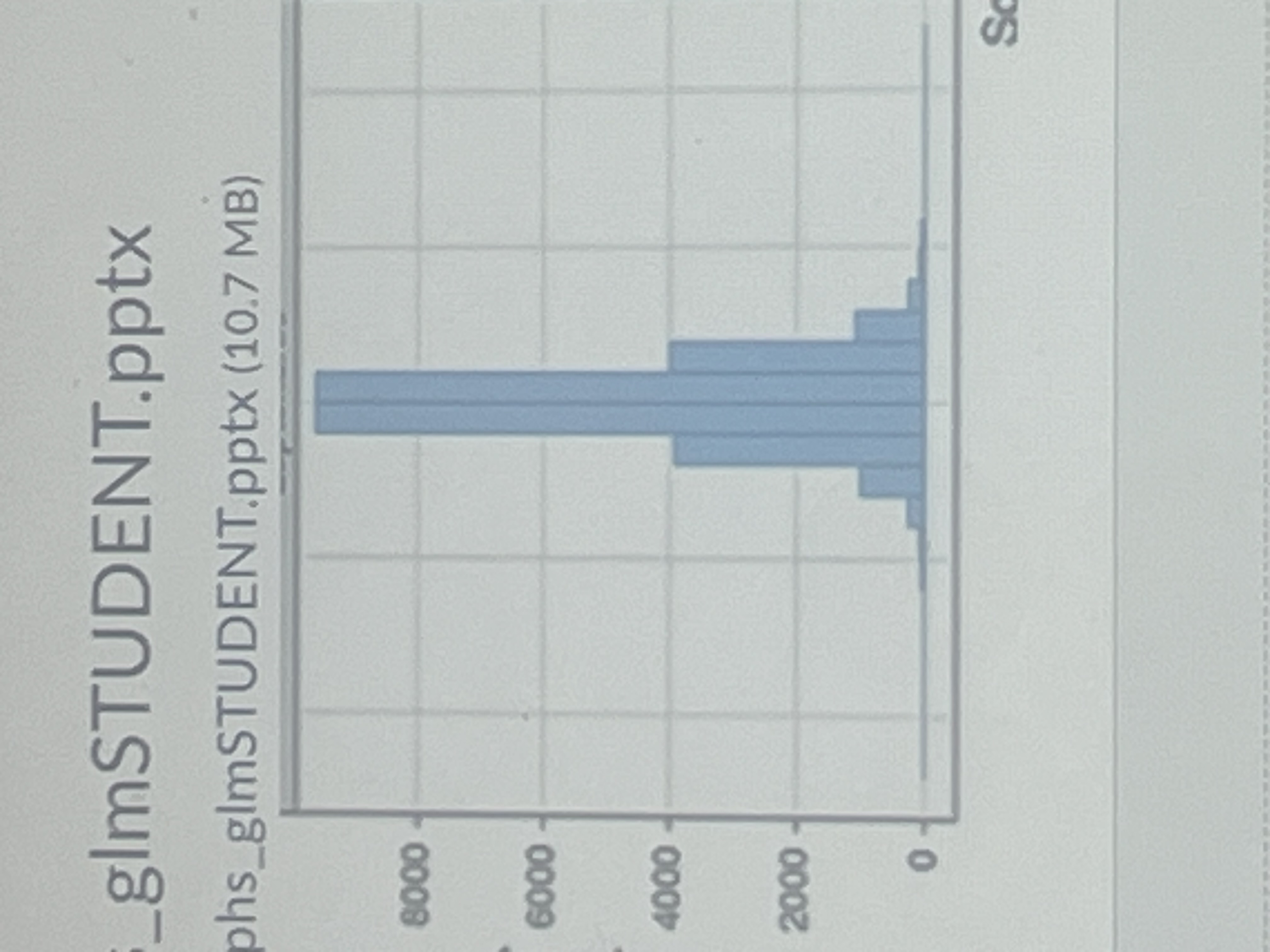
Leptokurtic

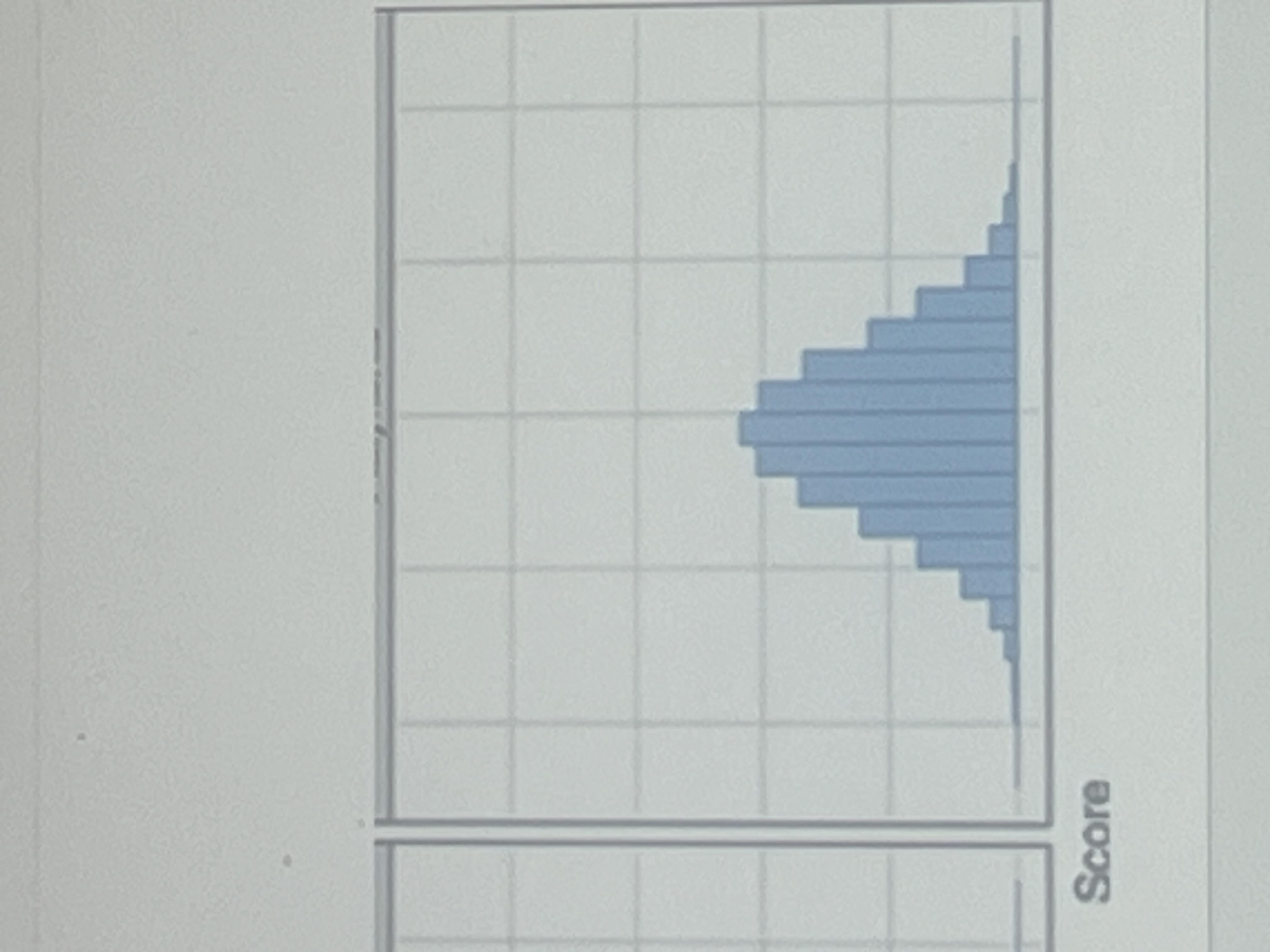
Platykurtic

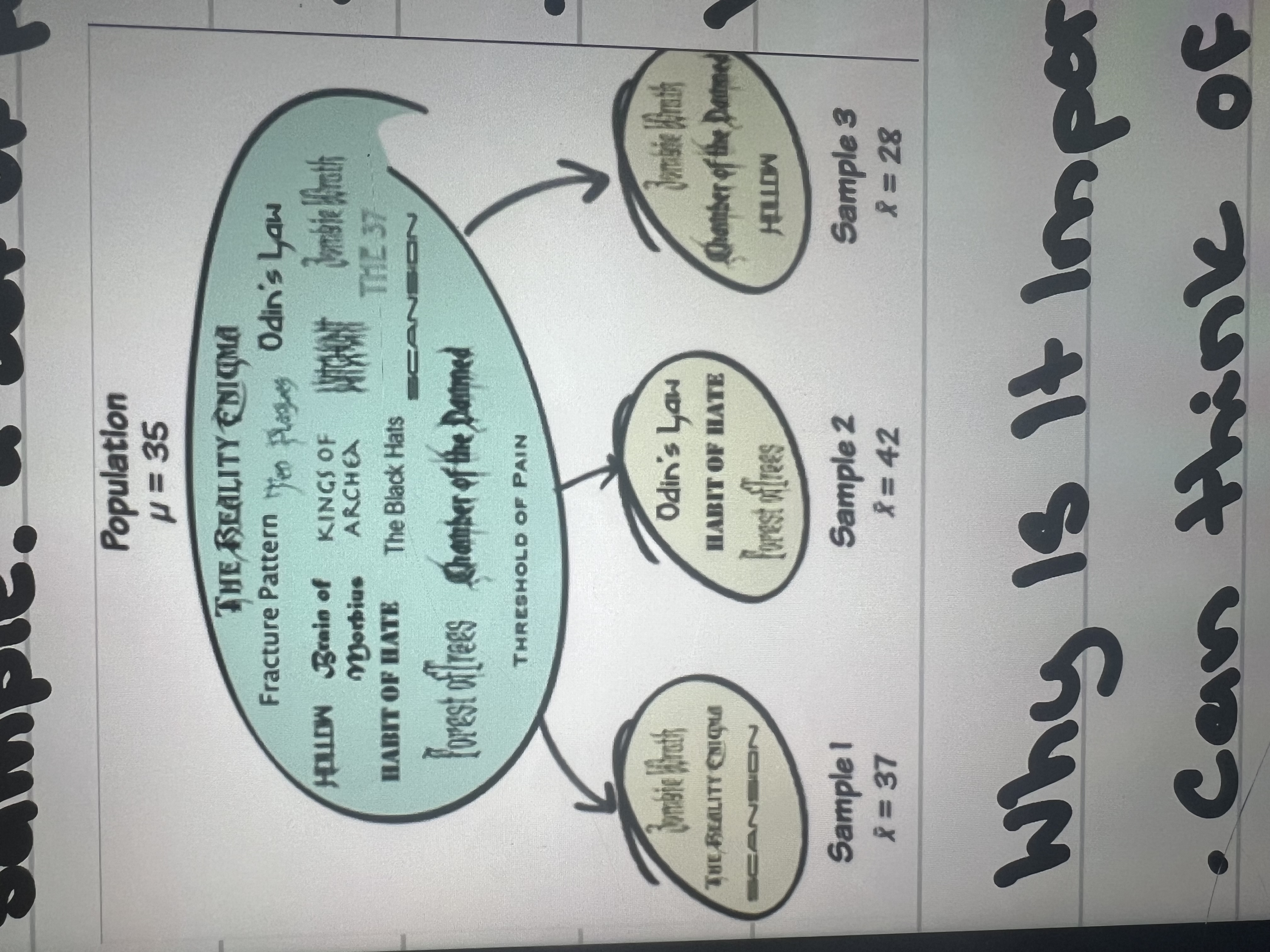
Population

The group of people you wanna study (eg. First year university students in Canada.)

Sample

A set of people from the population you want to study (eg. First year, Ontario Tech student students.)

Sampling variation

Statistics varying across different samples

Xi - mean

deviation equation

adding Deviations in a model

Will always equal 0 because some are positive and some are negative

SS equation (sum of squared errors)

Sum of squared deviations

Variance equation

SS (sum of squared deviations) divided by n-1

Sample standard deviation equation (S)

= square root of SS divided by n-1

Is S and SD the same thing

Yes

What does it mean if data is clustered close together

Standard deviation is smaller

What does it mean if data is clustered far apart

Standard deviation is larger

What does Z score do

Interprets score in the context of their distribution (mean and standard deviation)

Distribution of Z score

Mean of 0 and standard deviation of 1

Z score equation

Score-mean divided by standard deviation

What does it mean if Z score is postive

It’s above the mean

What does smaller z score mean

It’s closer to the average

What does z score tell us

The location of a score within a distribution

What percent of scores fall between 1.96

5%, 2.5% on each side (positive and negative)

Standard error

Tells us the similarity of estimates from different samples

If standard error (SE) is small what does that mean

Samples produce similar estimates (tightly pooled together) good

Large SE

produce very different estimates (bad) (need a larger estimate to capture that 95%)

Confidence intervals

Gives an estimated range of values which likely includes the mean

Confidence interval equation

Mean (+/-) (1.96*standard error)

What does correlation do

Examines association between 2 variables (ranges form -1 to 1)

What does covariance do

Quantify a relationship between correlation variables

What does it mean if convince deviate from the mean by the same amount

They’re likely to be related

What does R2 (r squared) mean

Represents correlation. Squaring the value of r gives you the proportion of variance in one variable shared by another

Issues of correlation

Third variable problem and direction of causality

Third variable problem

Causality can’t be assumed

Direction of causality

Correlation coefficients say nothing about which variable causes the other to change

R= .1

Small effect (the effect explains 1% of total variance)

R= .3

Medium effect (the effect accounts for 9% of total variance

R= .5

Large effect ( the effect accounts for 25% of the variance)

What is a regression

A way of predicting the value of a variable from another

Why do we use regression

To predict values of a dependent variable from one or multiple predictors

Any straight line can be defined by

The slope b1 and the y intercept b0

Slope (b1) tells us

The direction of the relationship and the strength (if it’s really steep, there’s a stronger relationship between the predictor and outcome)

The intercept b0 tells us

Where the line starts

b0 =

Y intercept

Yi=

Score of y for an individual score

Xi=

Score of x for individual score

B1=

Slope (effect)

Ei=

Error

Why do we have an error

Bc not every person will fit perfectly on the line

Flat line means

No relationship

x variable for regression is

The predictor

Y variable of regression is

The outcome

Sst (total variability) is

Distance between the data and the mean of Y

SSR (residual error variability) is

Difference between regression model and the actual data (if the number is big then regression line isn’t good)

If SSm is large that means

Linear model has made a big improvement to how well the outcome variable can be predicted

If SSm is small it means

using the linear model is little better than using the mean

Ssm (SSmodel) looks at what

Model variability (difference in variability between the model and the mean) relationship between regression and the mean

mean squared errors (MS) equation

Ss divided by df

MSM means

Mean squared model

MSR means

Mean squared residual

For the null what do we assume

The hypothesis is true (there’s not effect)

R squared

Tell us the preparation of variance of accounted for by a regression model (eg. If r squared is 0.483 that means this model (garlic worn) can account for 48.3% of the variation shared in the zombie approach times