Pre-Calculus Unit 1-3

function

each element in A is assigned to only one element in B

function A represents

input, independent, cause

function B represents

output, dependent, effect

vertical line test

test used to determine if a relation is a function - line must touch only 1 point vertically

horizontal line test

a test used to determine if the inverse of a relation is a function OR 1 to 1

if there are two solutions, is it a function?

no, it must only have one

what cannot be in the denominator of a function?

0

what is the range of a fractional function?

All real numbers, except for 0

what is the domain of a fractional function?

All real numbers, except for the root of the denominator

a closed circle means

greater than or equal to OR less than or equal to

a open circle mean

greater than OR less than

even degree

y-axis symmetry / ends behave the same: f(-x) = f(x)

odd degree

origin symmetry / ends behave opposite: f(-x) = -x

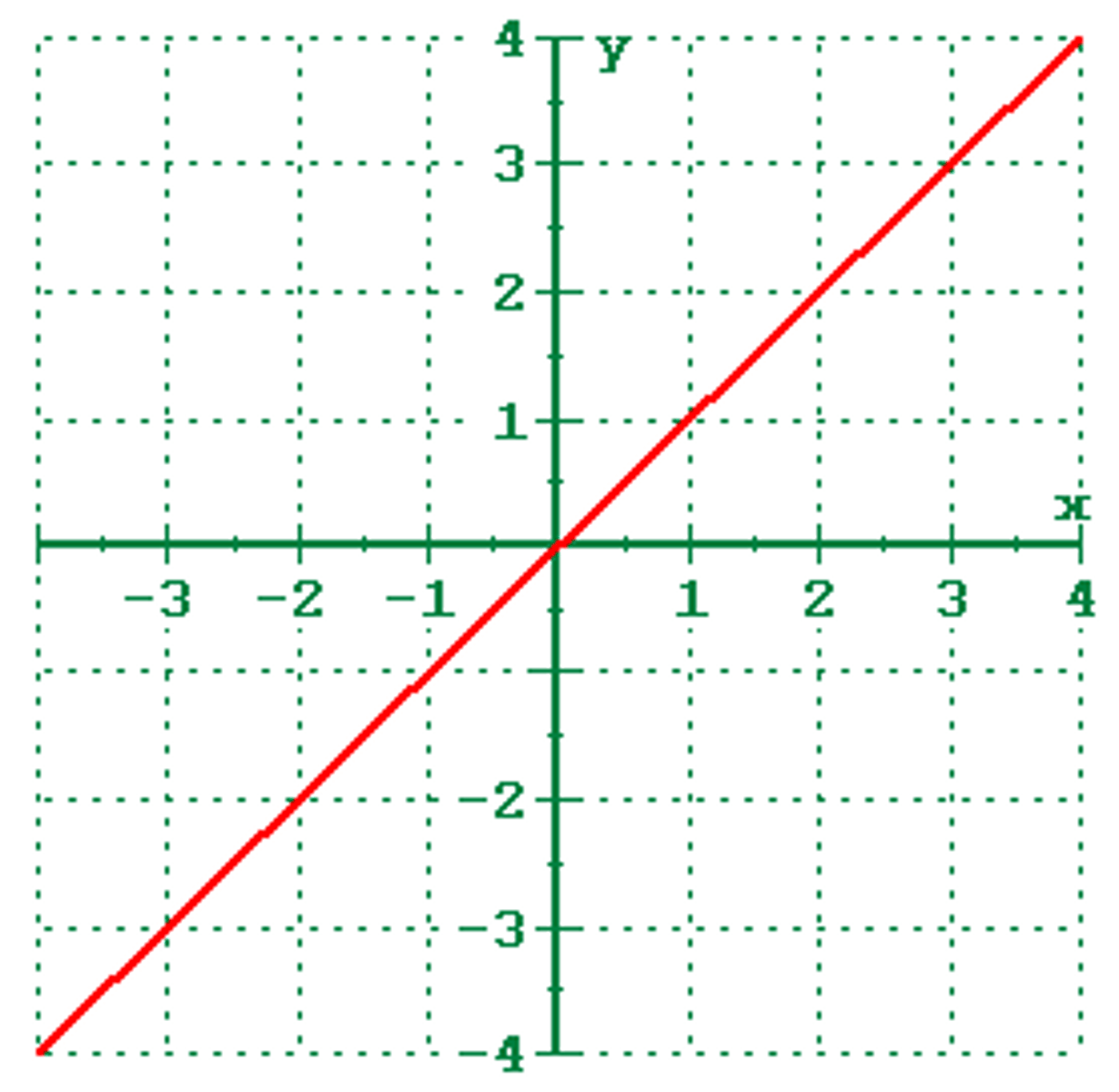
linear function

f(x) = mx + b

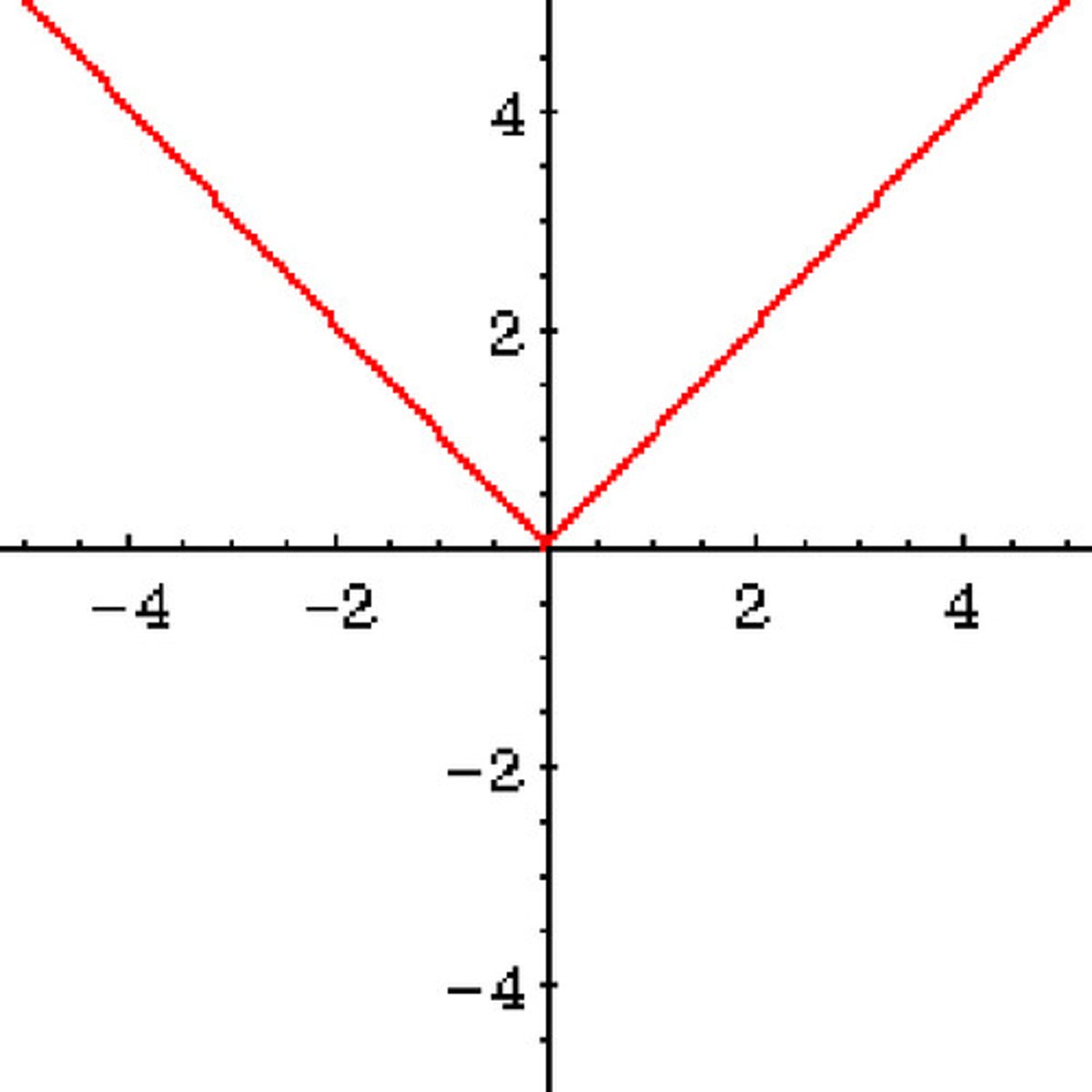
absolute value function

f(x) = a|x-h| + k

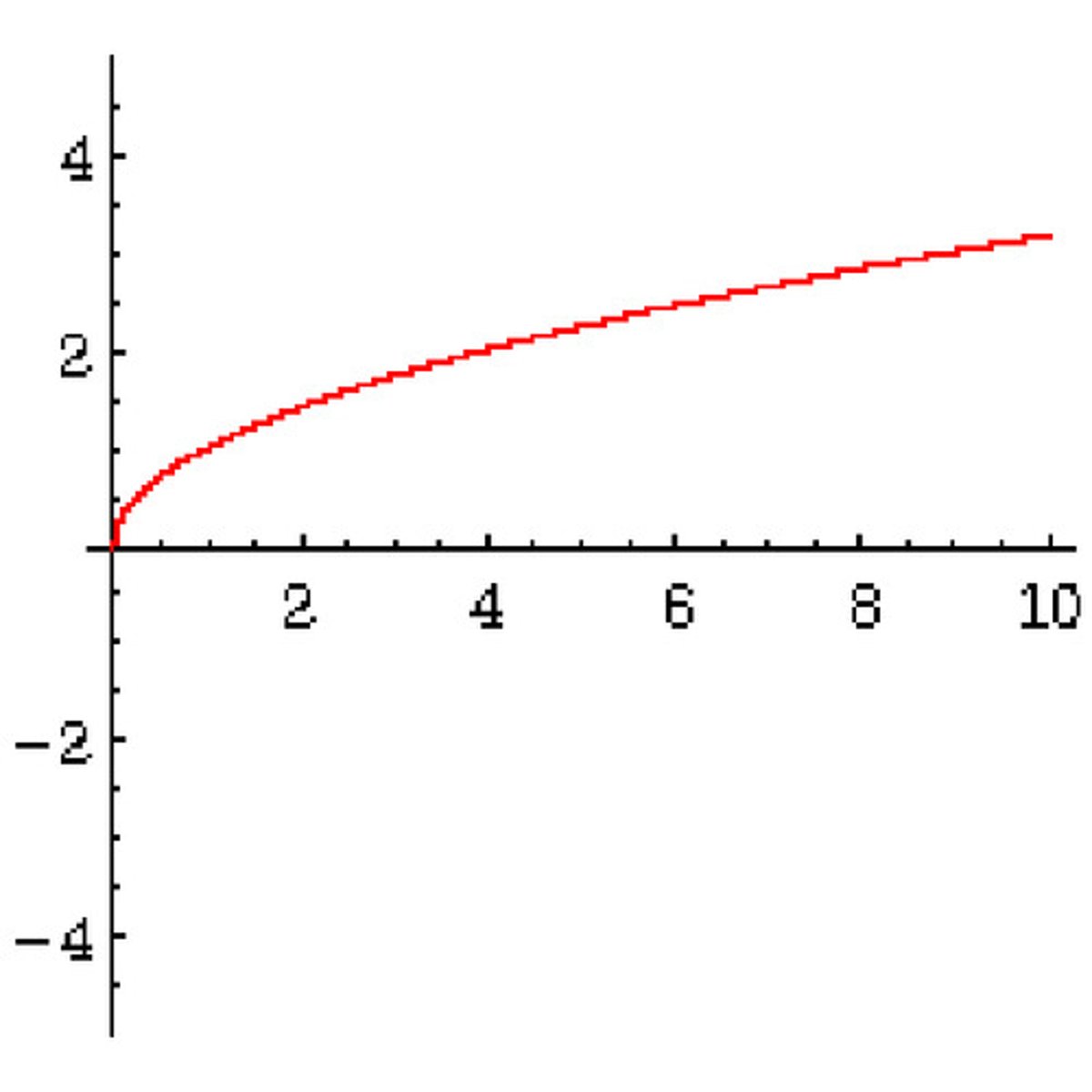
square root function

f(x) = a√x-h +k

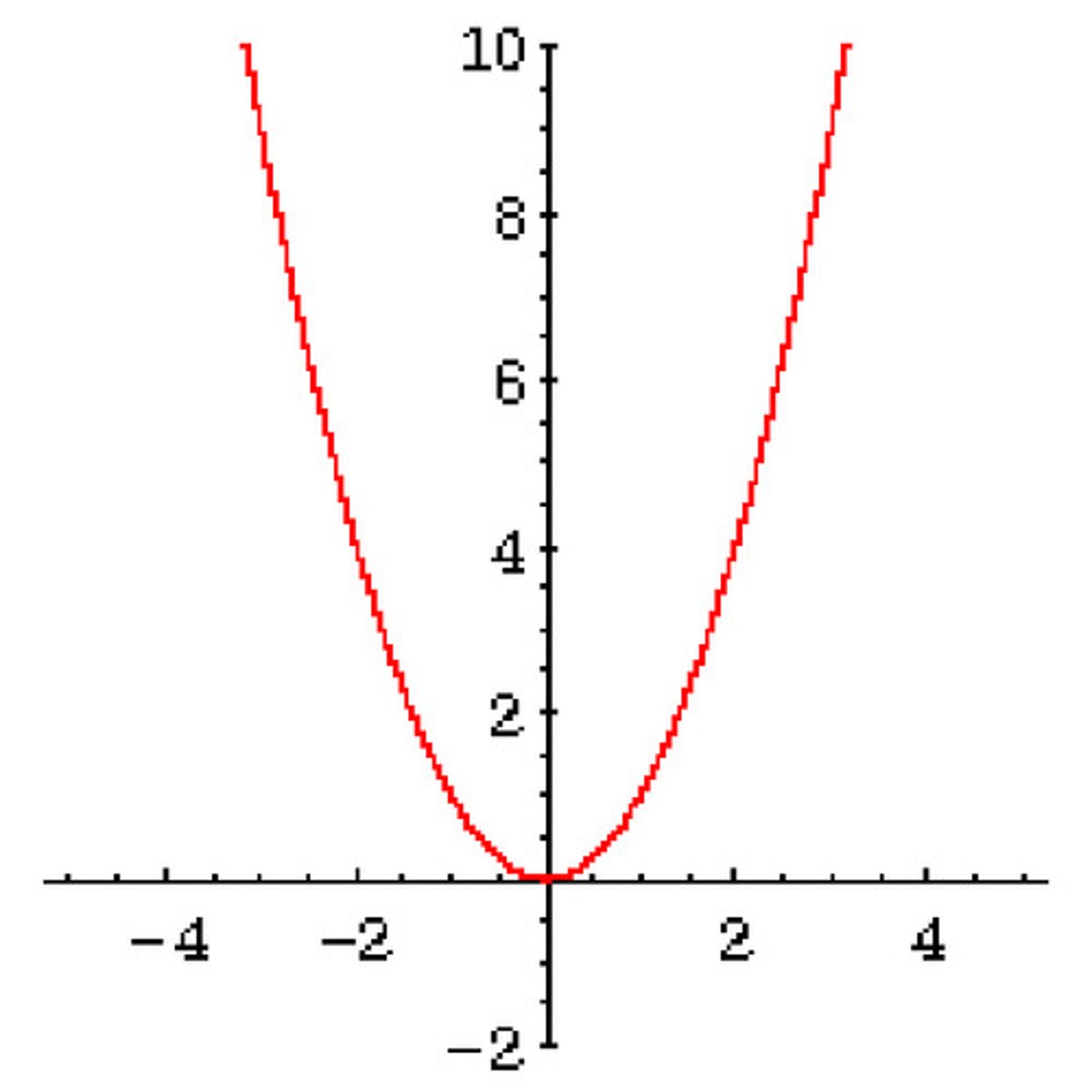
quadratic function

f(x) = a(x-h)^2 +k

cubic function

f(x) = a(x-h)^3 + k

rational function

f(x) = (a/x-h) +k

horizontal shift

f(x - h) OR f(x + h)

vertical shift

f(x) + k

nonrigid transformation (stretch/compression)

"a" value

x-axis reflection

-f(x)

y-axis reflection

f(-x)

f ￮ g (x)

f(g(x))

how to find domain of square root function?

set to 0 and solve

if f ￮ g (x) equals x, f and g are _____

inverses

how do you find the inverse of a function?

swap x and y

what switches between a function and its inverse?

the domain and range

standard form

f(x) = ax^2 + bx + c

what does c represent in standard form?

the y-intercept

parent quadratic function (function, domain, range, y-intercept, axis of symmetry, minimum)

y = x^2

D: (-∞, +∞)

R: [0, +∞)

y-int: 0

A.O.S: x = 0

minimum: at 0

how to find vertex in standard form

(-b/2a, f(-b/2a))

vertex form

f(x) = a(x-h)^2 + k

vertex: (h,k)

how do you find x-intercepts?

y = 0

how do you find y-intercepts?

x = 0

How to go from standard to vertex form

complete the square

even multiplicity

bounces on x-axis

odd multiplicity

crosses the x-axis

ways to factor

AC method, grouping, cubes, quadratic formula, GCF

when is a function continuous?

if there are no gaps, jumps, or sharp turns

steps for long division of polynomials (4)

1) add in any placeholders

2) look at 1st two numbers and find what makes them equal

3) distribute

4) swap signs then add

steps for synthetic division of polynomials (3)

1) find x = 0 (the zero)

2) bring down 1st number

3) multiple by the zero and add the numbers

what does the degree tell you?

how many solutions there are

how to list possible rational real zeros

factors of constant/factors of leading coefficient

Descartes rule of signs

count sign changes - negative/positive real roots

compare the degrees: Denominator = Numerator (horizontal and vertical asymptotes)

horizontal: leading coefficient

vertical: Denominator = o

compare the degrees: Denominator > Numerator (horizontal and vertical asymptotes)

horizontal: y = 0; +k

vertical: Denominator = o

compare the degrees: Denominator < Numerator (horizontal and vertical asymptotes)

horizontal: none; divide for slant

vertical: Denominator = o

what does a cancelled factor become?

a hole, a removable discontinutity

horizontal asymptote is a

what happens eventually (can be crossed)

vertical asymptote is a

brick wall (can't be crossed or touched)

steps to graph rational functions (6)

1) simplify

2) find and sketch asymptotes

3) plot x and y-intercepts

4) plot at least 1 point on either side of asymptote

5) use smooth curves

6) to find slant use long division

f(x) = a^x

a > o (always positive) - a ≠ 1 - cannot be imaginary

make a ______ to graph exponential growth

table

natural base e equals approximately

2.718

A = p(1 + r/n)^nt

A = new amount

p = principal (initial)

r = rate (decimal)

t = time (years)

n = number of times it compounds

A = pe^rt

continuously compounded

n = 1 (annual)

half life means

time it takes for element to decay in half

Change of base: loga(X)

logX/loga

loge(X) equals

natural log: ln(x)

if X is negative in log(X), what does it equal?

it does not exist (DNE)

B^E = N

logB(N) = E

logarithmic property: loga(1) = 0

a^0 = 1

logarithmic property: loga(a) = 1

a^1 = a

logarithmic property: loga(a^x) = x

a^x = a^x

logarithmic property: log(a^x) = log(a^y)

x = y

steps to graph logs (4)

1) change to exponential

2) select 'y' values 1st

3) use a table

4) find domain and range (D = the zero; R = all real numbers usually)

logarithmic property: loga(uv)

loga(u) +loga(v)

logarithmic property: loga(u/v)

loga(u) - loga(v)

logarithmic property: loga(u^v)

vloga(u)

steps to solve exponential and logarithmic equations (2)

1) rewrite in a form that allows solving for exponents/logs

2) one to one form (a^x = a^y so x=y)