Mathematics - Algebra and Functions

Graphs, Indices, Equations!

What are the Index Laws?

→ a^b x a^c = a^b+c
→ a^c / a^d = a^{c - d}
→ (a^c)^d = a^{c x d}
→ (ab)^c = a^c b^c

What must indices ALWAYS be for the index Laws to work correctly?

Indices must be RATIONAL.

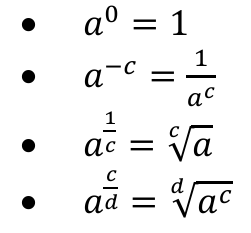
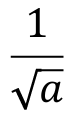
Rationalise this fraction.

answer.

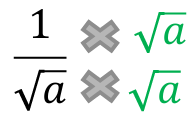
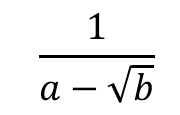
Rationalise this fraction.

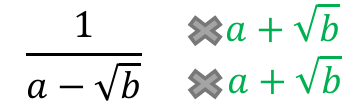
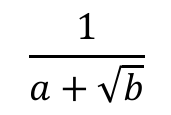
Rationalise this fraction.

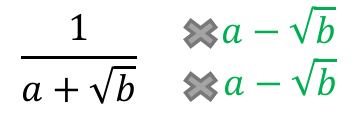
What is a Polynomial?

Finite expressions with POSITVE INTEGER indices.

State the Factor Theorem using algebra.

• If (x-p) is a factor of f(x), then f(p) = 0. and vice versa.

What is the difference between a theorem and a conjecture?

A theorem is a statement that has been proved.

A conjecture is a statement that is yet to be proved.

How do you write out a proof correctly in Math?

1. State known facts or theorems that are used in the proof.

2. Show logical steps, one after the other

3. statement of proof (final conclusion, using ∴)

What is an identity statement and how is it represented?

An identity means they will always equal to each other ; represented using ≡.

What do simultaneous equations imply on graphs?

The two graphs will intersect at a point/s, sharing same co-ordinates. Hence, solving simultaneous equations would give co ordinates of intersection.

When can Discriminant be used to prove number of intersections between two graphs?

When both graphs are quadratic (Quadratic simultaneous equations).

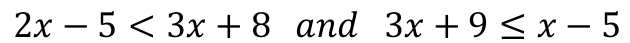
Solve this Linear Inequality.

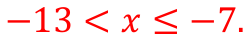
draw a graph of y = a/x.

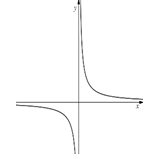
Draw graph of y = -a/x²

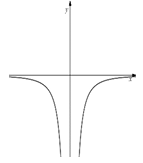
y = f(x) | Give vector for y = f(x+a)

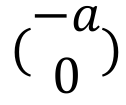
Give vector for y = f(x) + a

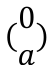
Give translation for y = f(-x)

Reflection of y = f(x) in y-axis

Give translation for y = af(x)

Stretched vertically by multiplier a.

Give translation for y = f(ax)

Stretched horizontally by multiplier 1/a.

Give translation for y = -f(x)

Reflection of y = f(x) in x-axis

Give turning point from this expression: (x+a)² - b

(-a, -b)

Give the number of roots for each of these:
→ Discriminant > 0
→ Discriminant < 0
→ Discriminant = 0

→ two real and distinct roots
→ No real roots
→ two real and equal roots