Binary Tree

binary tree

a tree-like hierarchical data structure such that each NODE stores a value (instance var value) and has at most two children: left and right (instance node vars)

• the left node stores a value less than the value of the node

• the right node stores a value greater than the value of the node

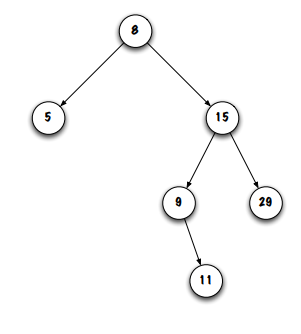
all nodes except ONE have exactly ______

one parent

a node that has no parent is called the _____

root

• drawn at the top of the diagram

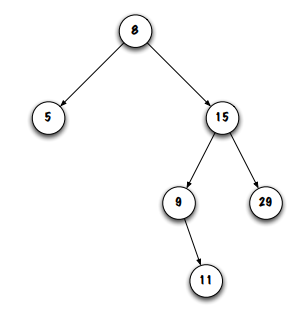
each node has ________ children

0, 1, or 2 children

nodes with no children are called _______

leaves (or external nodes)

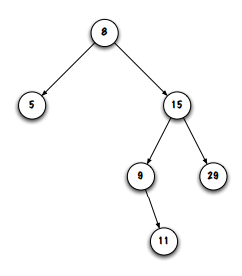
• in the image, 29 and 11 would be considered leaves

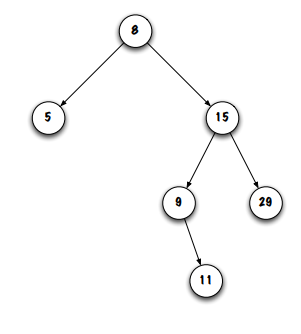
links between nodes are called ________

branches

a node and its descendents is called a ______

subtree

size of a binary tree

how many nodes are in the binary tree

• an EMPTY tree (no nodes) has size 0

binary trees can be defined ________

recursively

depth of a node

the number of links starting from the root that must be followed to reach that node.

• the root is the most accessible node. → the depth of a root is always 0

• the depth of “15” in the image is 1

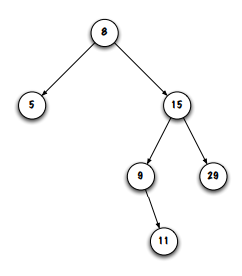
depth of a tree

depth of the deepest node

• here, the depth of the tree would be 3 (the level where “11” is"

binary seach tree

a binary search tree is a binary tree data structure such that:

• the nodes of a LEFT sub-tree only have elements that are less than the element stored at the local root of the subtree (or is empty)

• the nodes of a RIGHT subtree only have elems that are GREATER than the elem stored at the local root (or is empty)

• this means that a binary search tree has NO duplicates and is always ORDERED

binary search tree instance vars and nested node class

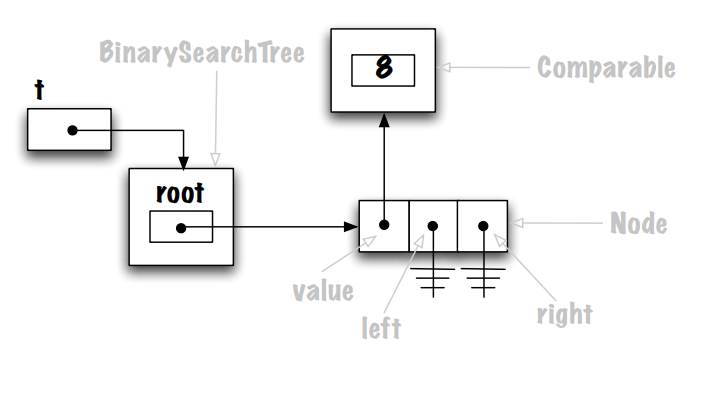
binary search tree memory diagram of a node

• note that this is a memory diagram of the root node with no children

binary search tree memory diagram of a tree

• each node has references to their left/right nodes (some refs are null, some are not)

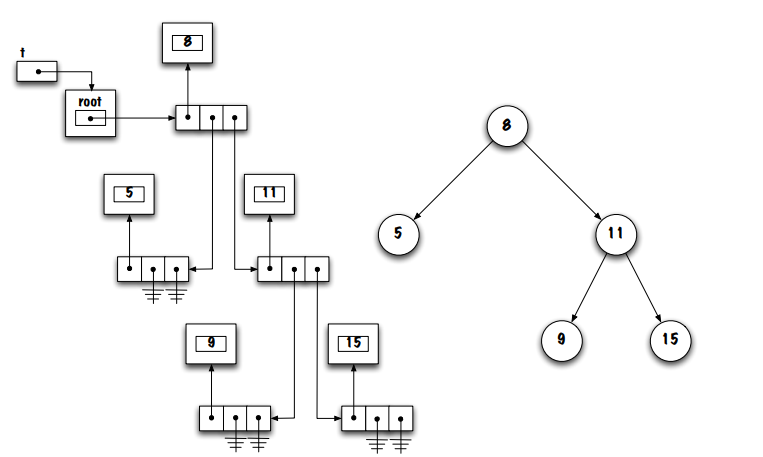
leaf node

a node where both left and right node references are null

how to tell if the tree is empty

if the root ref is null

boolean contains(E obj) (recursive implementation)

• returns true if the value is in binary tree

• “contains(obj, root)” calls the recursive method, which is a private method that can only be called from inside the class

recursive list processing main components

• starter method → calls the recursive method

• recursive method → almost always has one more parameter than the starter method

boolean contains(Node<E> current, E obj) (recursive implementation)

• the base cases:

  • if the elem is not in the binary tree (current == null)

  • if the elem is found (obj.compareTo(current.value) == 0)

• the recursive cases

  • if the value of obj is less than the current node (recursive call current.left)

  • if the value of obj is greater than the current node (recursive call current.right)

boolean contains(E obj) (non-recursive implementation)

three different ways to traverse a binary tree

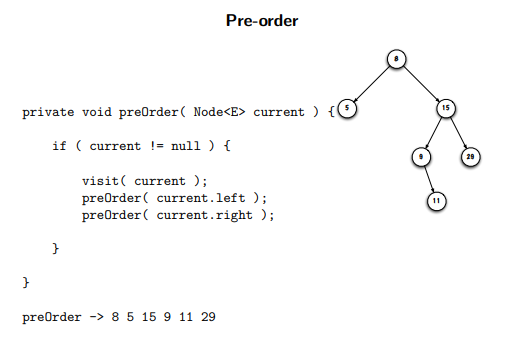
1. pre-order: current, left, right

2. in-order: left, current, right

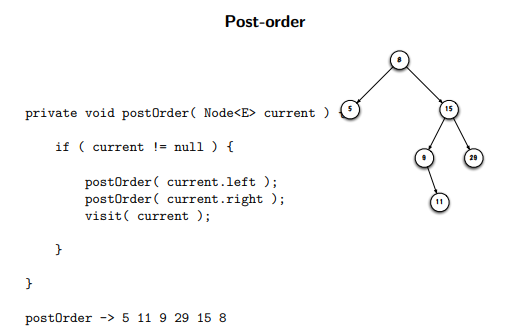
3. post-order: left, right, current

starter methods for tree traversal

• visit method is for printing the value of the node

• the order methods all call recursive methods that have the same name

binary tree traversal: pre-order recursive method

binary tree traversal: in-order recursive method

• remember that IN-ORDER prints the elems in the order of least to greatest (moving from left to right)

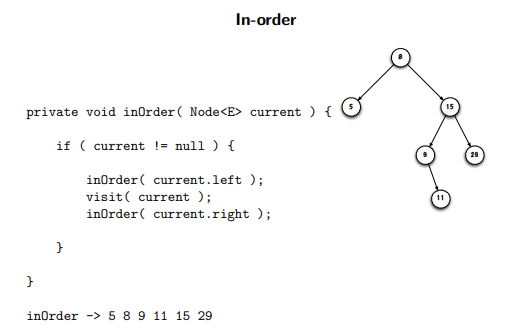
binary tree traversal: post-order recursive method

• go to the left-most node

• then go to the right most-node

• then go to root

• and repeat for subtrees

• check that you have accounted for EVERY NODE

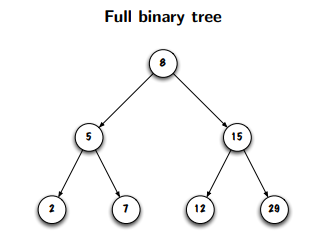
full binary tree

a full binary tree is when all nodes have exactly TWO CHILDREN except for the leaves

• meaning no nodes have just one child

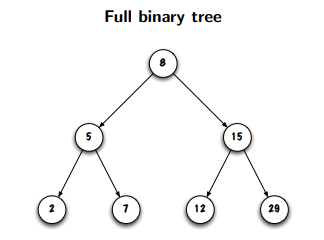
a balanced binary tree

• a binary tree of depth d is BALANCED if all the nodes at a depth <= d - 2 have exactly two children (not zero or one)

• the tree in the image is BALANCED bc the depth of the tree is 3, so every depth <= 1 has exactly 2 children

a balanced binary tree of depth d has

2^d to ((2^(d+1)) - 1) nodes

→ the size = 2^d to ((2^(d+1)) - 1)

the DEPTH of a balanced binary tree of size n (number of nodes in tree)

log₂(n)

the relationship b/w efficiency and whether or not the tree is balanced for the contains method

• a balanced tree would have better efficiency since the contains method eliminates a whole subtree with each comparison (divides the remaining nodes to traverse by 2, hence the efficiency being log₂(n)

methods that work better with recursion

• methods that follow a single path on the tree (from the root to some node) can easily be implemented w/o recursion

• methods that must visit more than one-subtree simultaneously are better w recursion (like toString which prints the tree out like an array)

boolean add(E obj): special case

• method adds an elem to the tree

• very similar to the contains method with the comparisons

• special case is if the tree is empty so the elem you add becomes the root → root = new Node<E>(obj)

boolean add(E obj): general case

• like the contains method, add follows a single path from the root to some node, so it does not need a recursive implementation

• always replaces null by a new value

• the structure of the tree is unchanged

Node<E> remove(E obj): 4 main cases

1. node (whose value == obj) has no sub-trees → remove the sub-tree

2. node has a left sub-tree ONLY → replace the node by that sub-tree

3. node has a right sub-tree ONLY → replace the node by that sub-tree

4. the node has two sub-trees → either replace with the value that immediately precedes (the value less than) or replace with the value that immediately follows (the value greater than)

consider that each case can have the value be the root, in which the replacement node must be referred to as the root

Node<E> remove(E obj): case for removing the root

• removeTopMost(Node<E> current) is where the bulk of the code is

Node<E> remove(E obj): pre-conditions

• the obj must not be null

• the tree must not be empty

Node<E> remove(E obj): case for if the obj is not found at root

Node<E> remove(E obj): general case for finding the node to remove

• first if-statement is for if the obj-to-be-removed is found

• second if-statement is for if you still need to traverse

Node<E> removeTopMost(Node<E> current)

• first checks if “current” only has one subtree

E getLeftMost(Node<E> current)

→ recursively finds the left-most node

Node<E> removeLeftMost(Node<E> current)

→ recursively finds and removes the left-most node

• “parent” always points to the node that was the previous node that “current” pointed to

• replaces the left-most node with its right neighbour

PreOrderIterator

• this code does not include the next() and hasNext() methods

PreOrderIterator nested class: boolean hasNext()

PreOrderIterator nested class: E next()