Chapter 1-SOLID MENSURATION FORMULAS

(edge)² A=a²

Area of a square

4 (edge) P=4(a)

Perimeter of a Square

base x height A=bh

Area of a Rectangle

2 (base + height) P=2(bh)

Perimeter of a Rectangle

½ base x altitude A=1/2 bh

Area of Right Triangle

a²+b²=c²

Pythagorean theorem

½ base x altitude A=1/2 bh

Area of an oblique triangle

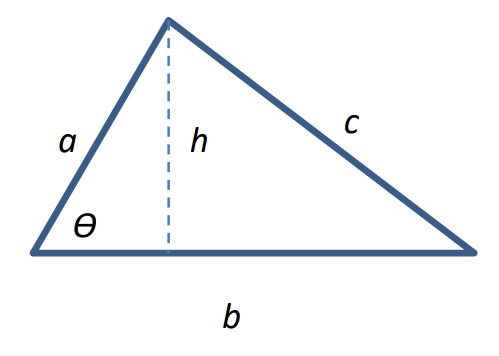
A=½ absinθ

Area of an Oblique Triangle, given two sides a and b included angle θ

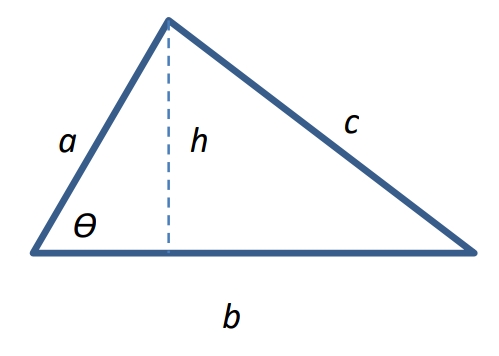
A=√s(s-a)(s-b)(s-c)

(Heron’s Formula) Area of an Oblique Triangle, given three sides a b and c

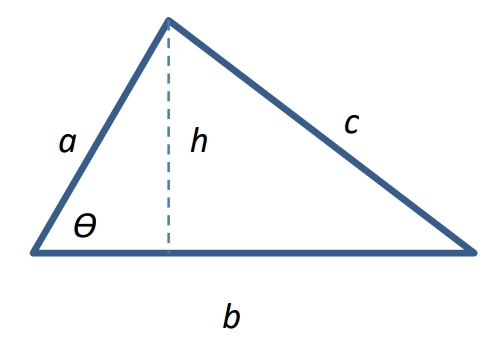
a+b+c/2

(Heron’s Formula) s

base x altitude A=bh

Area of a Parallelogram

1/2 sum of bases x altitude A=1/2 (a+b)h

Area of a Trapezoid

A=πr²

Area of a Circle (Given:radius)

C=2πr

Circumference of a circle (Given:radius)

2(radius) d=2r

diameter of a circle

π/4 (diameter)² A=πd²/4

Area of a Circle (Given:diameter)

C=πd

Circumference of a Circle (Given: diameter)

½ radius x arc A=1/2 rC or A=1/2 r²θ

Area of the sector of a circle θ in radians

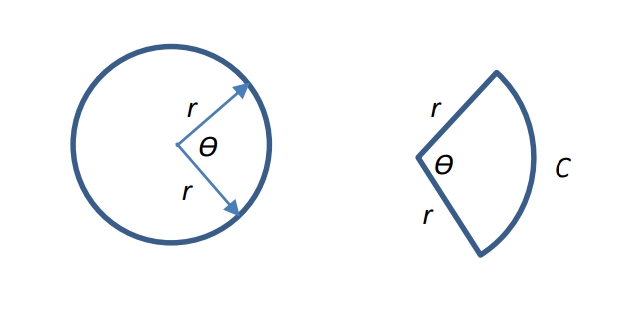
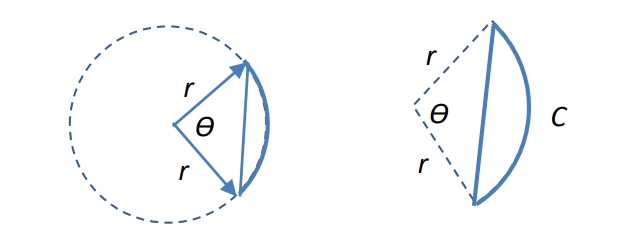
Area segment = Area sector − Area triangle

Segment of a Circle, θ is in radians

Area πld

Parabolic Segment