(digital) math sat practice

formula/content *must know* for the math portion of the dsat; content sourced from: Scalar Learning (YT), Epic Prep (YT), LearnSATMath (YT), Google, The College Panda (textbook), ChatGPT, & Lance Sakarda (YT).

point-slope form

y - y1 = m(x - x1)

*use when you have the slope and a coordinate

same slope, different y’s

parallel lines

point-slope form

y - y1 = m(x - x1)

*use when you have the slope and a coordinate

same slope, different y’s

parallel lines

circle formula

(x - h)² + (y - k)² = r²

(h, k) = center of the circle

r = radius

slope of a line when given coordinates

m = y₂ - y₁ / x₂ - x₁

slope intercept form

y = mx + b

m = slope → rise/run

b = y-intercept

midpoint formula

(x₁ + x₂ / 2 , y₁ + y₂ / 2)

*midpoint = average of two points

distance formula purpose

to find radius of circle, given center point/one exterior; to find hypotenuse w/o pythagorean theorem

distance formula

d = √(x₂ - x₁)² + (y₂ - y₁)²

length of an arc formula

L = (n/360)2πr

n = angle made by r; L = arc length (ex: crust of the pizza slice)

area of a sector

A = (n/360)πr²

A = area of the slice of pizza

n = angle given of sector

find values of x from quadratic equation

1. factor

ax² + abx + ab = 0

(ax + b)(x + a)

ax + b = 0; x + a = 0

(the last ab value = c for this example)

2. quadratic

1/2(a) (-b ± √b²-4(a)(c))

when quadratic equation = 0, x values are the solution

(you don’t need to multiply by 1/2a as long as you divide everything by 2a—it’s the same thing, written this way to accommodate formatting limitations)

quadratic standard form

y = ax² + bx + c

when quadratic equation = 0, x values are the solution

soh cah toa

sine = opposite/hypotenuse

cosecant = hypotenuse/opposite

cosine = adjacent/hypotenuse

secant = hypotenuse/adjacent

tangent = opposite/adjacent

cotangent = adjacent / opposite

similar triangles (same angles + proportionate side lengths)

sine of corresponding angles are equal

probability

number of favorable outcomes / total number of outcomes

exponential growth

y = a(1 + r)^t

a = initial value; r = growth rate; t = time

exponential decay

y = a(1 - r)^t

a = initial value; r = decay rate; t = time

vertex of a parabola formula when in quadratic standard form

(x, y)

x = -b/2a

y = x plugged back into the original equation (that you got the b and a values from)

vertex form

y = a(x - h)² + k

vertex: (h, k)

pythagorean theorem

a² + b² = c²

a & b = legs

c = hypotenuse

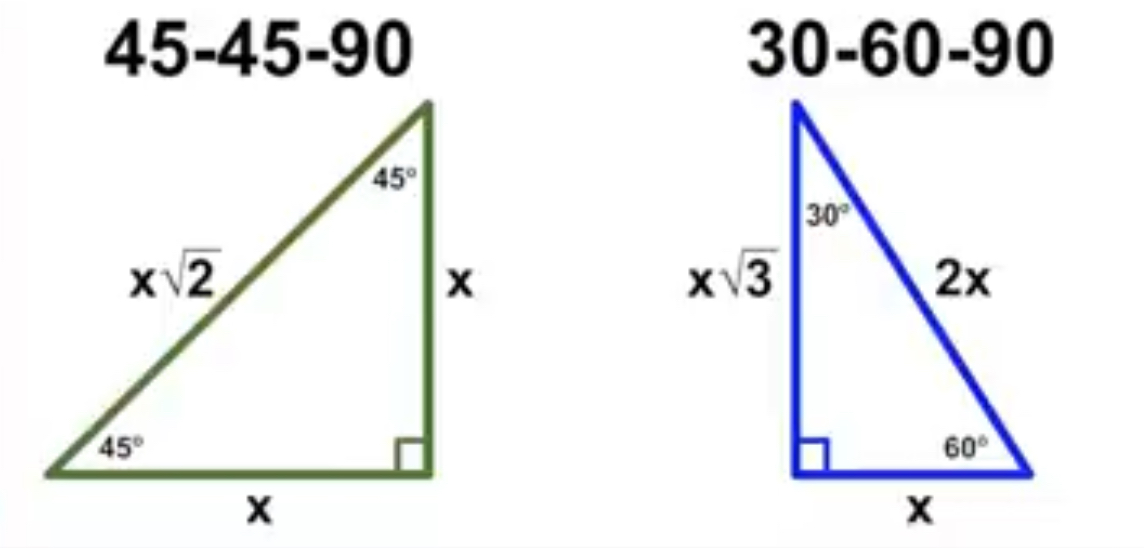
special right triangles

45º-45º-90º → leg 1: x, leg 2: x, hypotenuse: x√2

• hypotenuse ÷ √2 = leg

30º-60º-90º → small leg: x, big leg: x√3, hypotenuse: 2x

• small leg x √3 = big leg

• big leg ÷ √3 = small leg

• small leg x 2 = hypotenuse

distance formula (rate)

d = rt

d = distance; r = rate (rate = speed); t = time

*units of rate must equal units of time

sine/cosine relationship

*sin(x) = cos(90 - x)

x = angle

90 - x = complement of that angle

sin(10) = cos(80)

sin(20) = cos(70)

sin(30) = cos(60)

sin(40) = cos(50)

sin(50) = cos(40)

sin(60) = cos(30)

sin(70) = cos(20)

sin(80) = cos(10)

*equals 90º → definition of complementary angles: two angles that up to 90º

sum of solutions of quadratic

0 = ax² + bx + c

sum of solutions = -b/a

product of solutions of quadratic

0 = ax² + bx + c

product of solutions: c/a

discriminant (of quadratic)

0 = ax² + bx + c

b² - 4(a)(c)

discriminant = stuff under the radical in quadratic formula

find number of solutions (quadratic)

use discriminant to solve

x < 0 (negative; imaginary solutions) → no real solution

x = 0 → one real solution

x > 0 (positive) → two real solutions

area of equilateral triangle

∆ → all sides equal s

area of equilateral triangle = s²√3/4

pythagorean triples

3-4-5

• 6, 8, 10 (× 2)

• 9, 12, 15 (× 3)

• 12, 16, 20 (× 4)

• 15, 20, 25 (× 5)

5-12-13

• 10, 24, 26 (× 2)

• 15, 36, 39 (× 3)

• 20, 48, 52 (× 4)

• 25, 60, 65 (× 5)

7-24-25

• 14, 48, 50 (× 2)

• 21, 72, 75 (× 3)

• 28, 96, 100 (× 4)

• 35, 120, 125 (× 5)

8-15-17

• 16, 30, 34 (× 2)

• 24, 45, 51 (× 3)

• 32, 60, 68 (× 4)

• 40, 75, 85 (× 5)

*multiply all sides by a value to find the sides when you know its a pythagorean triple

perpendicular slope

slope → m = a/b

perpendicular slope (opposite reciprocal of slope) → m = -b/a

slope of parallel lines

slope → m = a/b

parallel slope → m = a/b

*slopes are the same

sum of angles formula (for any polygon)

sum = (n - 2)180º

n = number of sides

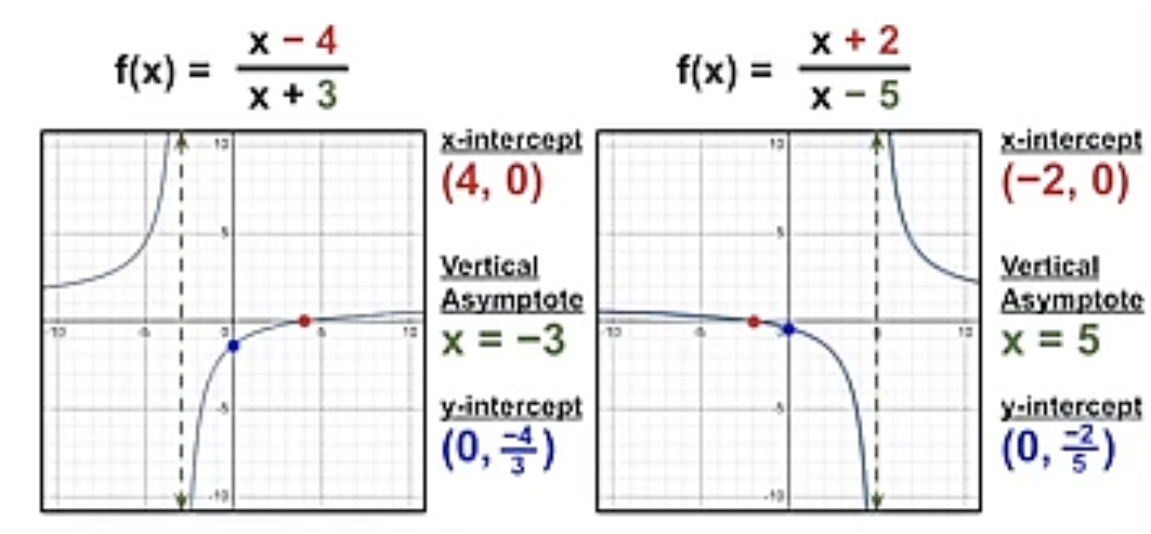
rational functions

x-intercept

• equation: set numerator equal to zero

• graph: where the line touches the x-axis (same as the zeroes)

y-intercept

• equation: plug in 0 for x in the equation

• graph: where the line touches the y-axis

vertical asymptote

• equation: set denominator equal to zero

• graph: find the line the function is approaching but never meeting

horizontal asymptote

• equation: f the degree of the numerator is less than the degree of the denominator, it’s y = 0; if the degree of the numerator is equal to the degree of the denominator, y = leading coefficient/leading coefficient; if the degree of the numerator is greater than the degree of the denominator, there is no horizontal asymptote)

• graph: find the line the function is approaching but never meeting

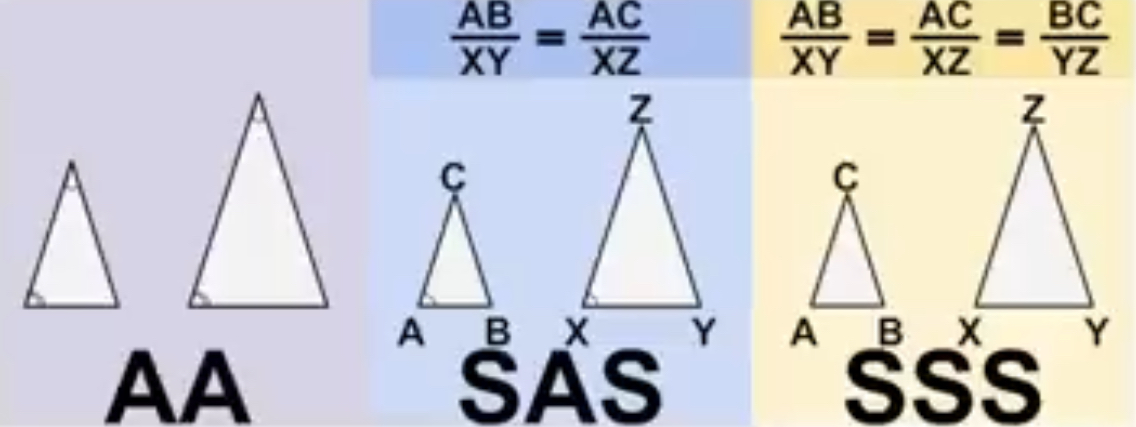
triangle congruence theorems

SSS - side-side-side

SAS - side-angle-side

ASA - angle-side-angle

AAS - angle-angle-side

HL - hypotenuse-leg

*the letters of these theorems must be in this exact order

triangle similarity theorems

SSS - side-side-side

SAS - side-angle-side (congruent angles, proportionate sides)

AA - angle-angle

*sides proportionate and not congruent; angles are always congruent

unit circle

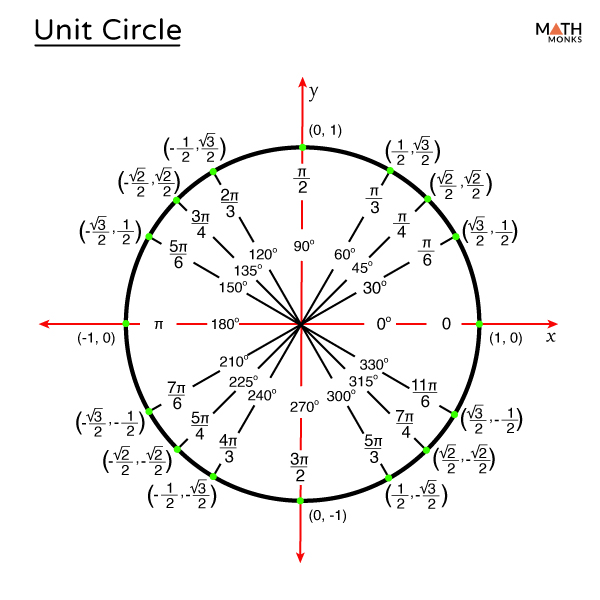
sin(Θ) = y-value (y / r)

cos(Θ) = x-value (x / r)

tan(Θ) = y / x

exponent rules (7)

x^a • x^b → x^a+b

(x^a)^b → x^a•b

x^a / x^b → x^a-b

x^-a → 1 / x^a

x⁰ → 1

x¹ → x

x^a/b → b√x^a

absolute value

|ax - b| = c

• two equations:

  • ax - b = c

  • ax - b = -c

• solve for x → two solutions

inequalities

-ax - b < c

*-ax < b+c

*when dividing (or multiplying) -a on both sides, you have to switch the sign

*answer: x > b+c/a

solutions in systems of equations

no solution = parallel lines (same slope)

infinite solutions = same line (same slope, same y-intercept)

one solution = lines intersect at a single point (different slopes)

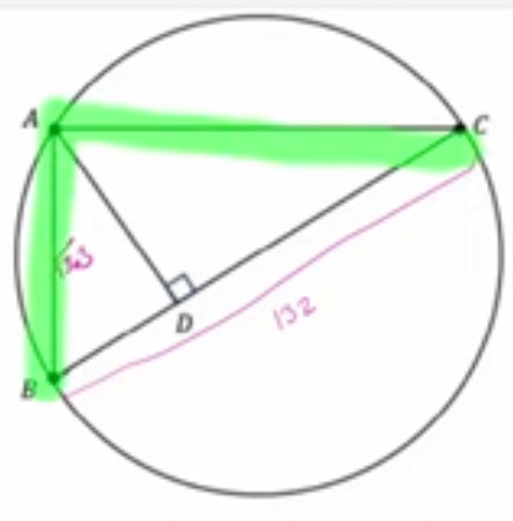
inscribed angle theorem

any inscribed angle that extends from the same arc as the center angle will always be ½ of the center angle

inscribed angle theorem of the diameter

if a point lies on the circumference and is connected to the endpoints of the diameter, it forms a right angle with the diameter

simple interest formula

A = p (1 ± r)^t

A = amount; p = principal amount; r = rate; t = time

compound interest formula

A = p (1 ± r/n)^nt

A = total amount; p = principal amount; r = rate; n = number of times interest is applied per time period; t = time

integer vs. non-integer

integer: positive/negative whole number (including zero)

non-integer: not a whole number/zero; decimal or fraction

use vertex form for quadratic (minimum or maximum)

y = a(x - h)² + k

positive a: parabola opens upwards and k represents the minimum value

negative a: parabola opens downwards and k represents the maximum value.

when there’s one solution between a quadratic and horizontal line

the solution is at the vertex (its x-value, unless the y-value is asked for)

when to use desmos for no solution problems

quadratic = YES

systems of equations (linear) = NO (just make the slopes equal)

percent change formula

percent change = 100% (new value - original value / original value)

*if the problem is worded as “percent greater/less than,” the quantity that comes after “than” should be taken as the original value

p% of x

p/100 × x

p% greater than x

(1 + p/100)x

p% less than x

(1 - p/100)x

square inscribed in a circle

the diagonal of a square is equal to the diameter of the circle it is incribed in

square relationship between its diagonal and side lengths (formula)

d = s√2

d = diagonal / diameter; s = side length

when to use desmos

• finding the vertex (graph)

• x/y-intercepts (graph)

• quadratics that intersect at 1/0 points (graph)

• finding (basic) mean/median (built in feature, check “functions”)

• finding points on a circle (graph)

• systems of equations/inequalities (graph)

  • don’t use when there are more than two variables unless you are extremely well-versed in demsos and know how

• number of solutions (graph)

• (note: there’s probably more ways to use desmos, but to keep it short: use it for most function problems, to check your work, and whenever YOU think you can fit it into some random problem to solve—that said, a normal calculator is quicker to operate for basic math like +/-/÷/× and desmos DOES NOT work for every problem type—look into YT videos for specifics on this—and DO NOT waste your time if you’re confused when to use it, but you had better know how)

180º

equals π radians

degrees/radians conversion

degree = radian × 180/π

radian = degree × π/180

standard deviation

the spread of data from the mean

standard form of a linear equation in one variable

ax + by = c

a = coefficient of x (cannot be 0)

x = -b/a

b = constant term

y = when x = 0

c = constant

average rate of change formula

rate of change = change in y / change in x

zero of a linear function

*when y equals 0

0 = mx + b → x = -b/m

systems of equations

1. USE DESMOS FIRST—IT WILL ALMOST ALWAYS SAVE YOU TIME FOR THESE PROBLEMS; to do so, just plug in both equations in, separately, and find the value you need/solve accordingly (see where the lines intersect one another or the x/y-intercepts)

   • that said, use the traditional methods, below, if you can’t use desmos to solve it for whatever reason

2. substitution method: solve for x or y for one equation → plug whatever x or y equals in the other equation’s x or y to find the variable you don’t have → find the initial variable you solved for by plugging in the variable you just found (so you get an actual number)

3. elimination method: multiply both equations by a value that makes either the x’s or y’s the same number but with opposite signs (ex: multiplying the top equation by 3 to get 6x and the bottom equation by -6 to get -6x so they cancel out and you solve for y)—all of the numbers/variables are multiplied by the relevant number of your choosing → plug this equation into the smaller/easier equation to get one variable → plug in this value into one of the equations to find the other variable

linear standard form

Ax + By = C

linear standard form to slope-intercept form

Ax + By = C → y = -A/Bx + C/B

slope-intercept form to linear standard form

y = mx + b → mx - y = -b

y = 0/singular number

straight horizontal line; line goes infinitely only carrying its y-value

x = 0/singular number

straight vertical line; line infinitely long only carrying its x-value

slope in standard linear equations

m = -a/b

m = slope; -a = negative a value; b = b value

(in this equation: ax + by = c)