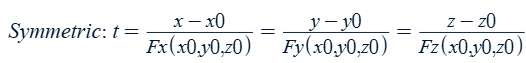Unit 3 Calculus 2

Surface area of the plane curve parametrized by x = f(t) and y = g(t), a ≤ t ≤ b, revolved about the x-axis

Tip: If only given f(x), let x = t and y = f(t)

Function of several variables

Two: z = f(x,y)

• z₀ = f(x₀,y₀)

Three: w = f(x,y,z)

Notation for domain graphs

Solid line for an included value (≤, ≥)

• ex. x ≥ 0 for √x

Dotted line for an excluded value (<, >, ≠)

• exs. x > 0 for ln(x) and x ≠ 0 for 1/x

* On the xy-plane for f(x,y), so find what x and y can/cannot be

* Inequalities are otherwise graphed like equations.

Level curve vs. level surface

Level curve - a function of two variables with a constant value

• f(x,y) = k

• 2-D

Level surface - a function of three variables with a constant value

• f(x,y,z) = k

• 3-D

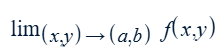
Determining the limit (a z-value) of f(x,y)

Check paths along the…

• x-axis, where y = 0

• y-axis, where x = 0

• x = y line

If all three paths approach the same value as (x,y) tends to (a,b), then that might be the limit. Use the squeeze theorem to be certain. If not, then the limit does not exist.

* A constant tends to itself.

Squeeze theorem

Conditions: L ≤ |f(x,y)| ≤ |g(x,y)|

• L - possible limit

• f(x,y) - the given function

• g(x,y) - a function similar to f(x,y)

  • Tip: Eliminate a term that prevents 0/0.

If |g(x,y)| → L as (x,y) → (a,b), then the limit is indeed L.

* Factor variables with odd exponents into evens and ones so that it’s only necessary to take the absolute value of variables raised to the first power.

f(x,y) is continuous at (a,b) if…

i.e. direct substitution does not yield indeterminate form (0/0 or ∞/∞)

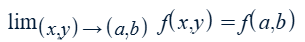
Partial derivatives of f(x,y,(z))

With respect to x:

• f_x(x,y,(z)) or ∂f/∂x

• y (and z) are fixed

With respect to y:

• f_y(x,y,(z)) or ∂f/∂y

• x (and z) are fixed.

(With respect to z:)

• f_z(x,y,z) or ∂f/∂z

• x and y are fixed

* Treat fixed variables as constants.

Second order partial derivatives for f(x,y)

f_xx = (f_x)_x = ∂/∂x(∂f/∂x)

f_yy = (f_y)_y = ∂/∂y(∂f/∂y)

f_xy = (f_x)_y = ∂/∂y(∂f/∂x)

f_yx = (f_y)_x = ∂/∂x(∂f/∂y)

* Derive with respect to the first variable, then the second, etc.

Clairaut’s theorem

The order of differentiation for the mixed partial derivatives of f(x,y) does not matter.

f_xy = f_yx

Slopes of the tangent line to the surface z = f(x,y) in the direction of…

• x-axis: f_x(a,b) is the slope of the tangent line to the curve z = f(x,b) (where y = b is fixed) at the point x = a.

• y-axis: f_y(a,b) is the slope of the tangent line to the curve z = f(a,y) (where x = a is fixed) at the point y = b.

Linearization and linear approximation of f(x,y) at point (x₀,y₀)

Linearization: L(x,y) =

Linear approximation: f(x,y) ≈

z₀ + f_x(x₀,y₀)(x – x₀) + f_y(x₀,y₀)(y – y₀)

Chain rule for f(x,y,(z)) when there’s one variable t

df = dz and ∂f = ∂z for z = f(x,y)

df = dw and ∂f = ∂w for w = f(x,y,z)

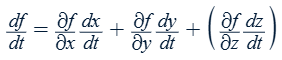
Chain rule for f(x,y,(z)) when there are multiple variables

Ex. with respect to t

∂f = ∂z for z = f(x,y)

∂f = ∂w for w = f(x,y,z)

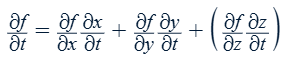
Implicit differentiation of level curves and surfaces

F(x,y) = 0

• dy/dx = - F_x(x,y) / F_y(x,y)

F(x,y,z) = 0

• ∂z/∂x = - F_x(x,y,z) / F_z(x,y,z)

• ∂z/∂y = - F_y(x,y,z) / F_z(x,y,z)

* Isolate everything to one side and call it F.

Gradient of f(x,y,(z))

▽f(x,y,(z)) = <f_x(x,y,(z)),f_y(x,y,(z)),(f_z(x,y,(z)))>

• vector-valued function

At point (x₀,y₀,(z₀)):

▽f(x₀,y₀,(z₀)) = <f_x(x₀,y₀,(z₀)),f_y(x₀,y₀,(z₀)),(f_z(x₀,y₀,(z₀)))>

• vector

Directional derivative of f(x,y,(z)) in the direction of unit vector u

D_uf(x,y,(z)) = ▽f(x,y,(z)) • u

Maximum directional derivative of f(x,y,(z))

D_uf = ▽f • u

D_uf = |▽f||u|cosθ

D_uf = |▽f||u|cos(0) ← θ = 0 because ▽f||u

D_uf = |▽f|(1)(1) ← the length of u is 1

D_uf(x,y,(z)) = |▽f(x,y,(z))|

Tangent plane at point (x₀,y₀,(z₀))

To f(x,y):

z = z₀ + f_x(x₀,y₀)(x – x₀) + f_y(x₀,y₀)(y – y₀)

.

To a level surface, F(x,y,z) = k ≠ 0:

F_x(x₀,y₀,z₀)(x – x₀) + F_y(x₀,y₀,z₀)(y – y₀) + F_z(x₀,y₀,z₀)(z – z₀) = 0

Normal (perpendicular) line to the level surface F(x,y,z) = k at point (x₀,y₀,z₀)

Parametric equations:

x = x₀ + F_x(x₀,y₀,z₀)t

y = y₀ + F_y(x₀,y₀,z₀)t

z = z₀ + F_z(x₀,y₀,z₀)t