BIEN135 Final Discussion Questions (Ch. 6-8)

6.1) Which of the following properties are extensive (choose all that apply):
a. temperature
b. pressure
c. amount of heat released
d. density
e. energy
f. molarity
g. number of moles
h. mass
i. volume

C, E, G, H, I

6.2) A piston containing an ideal gas expands isothermally from 7 atm pressure to 2 atm pressure. The energy of the system (that is, the contents of the piston) remains constant during this process. (True/False)

True

6.4) The enthalpy change for a process is equal to the heat transferred to the system under which of the following conditions?
a. constant volume
b. constant pressure
c. constant temperature
d. reversible expansion
e. expansion at a constant pressure followed by reversible compression

B

6.8) A reaction that releases energy is called an __________ reaction.

exothermic

6.10) Electrostatic interactions are governed by _______'s Law

Coulomb

6.12) The energy for van der Waals interactions approaches _______ as the distance between atoms goes to zero and approaches _______ at infinite distance.

infinity, zero

6.17) The complete oxidation of one mole of a sugar produces carbon dioxide and water. 2000 kJ of heat is transferred from the system to the surroundings. The rearrangement of bonds as 0.5 moles of the sugar are oxidized generates heat in an open test tube (101 J*L^-1 pressure and 300 K temperature). What is the change in internal energy of the system (ΔU)? What is the change in enthalpy of the system (ΔH)?

ΔU = q + w. There is no work done. Therefore:
ΔU = q = –2000 kJ•mol–1 × 0.5 mol released by the
system
ΔU = –1000 kJ
ΔH = ΔU + PΔV. Since there is no volume change,
ΔV = 0 and ΔH = ΔU = –1000 kJ.

6.19) How much kinetic energy does a system containing
3 moles of an ideal gas at 300 K possess? What is the
heat capacity at constant volume? How much heat
would need to be transferred to the system to raise the
temperature by 15°C?

K.E. = 3/2 nRT
= 3/2 × 3 mol × 8.31 J•K^(–1)•mol^(–1) × 300 K
= 11,218.5 J = 11.2 kJ
CV = 3/2 nR
= 3/2 × 3 mol × 8.31 J•K^(–1)•mol^(–1)
= 37.4 J•K^(–1)
q = CV × ΔT = 37.4 J•K^(–1) × 15 K = 561 J

6.25) A salt bridge between an arginine and a glutamic acid
has the two bridging atoms 3.5 Å apart. Assume that
these bridging atoms have elementary charges of +1
and –1, respectively. What is the energy if the residues are a) on the protein
surface (ε = 80) and b) in the core of the protein (ε = 2)?

a. U = 1/ε (qiqj/rijÅ) x 1390 kJ•mol^(–1)
U = 1/80(-1/3.5) x 1390 kJ•mol^(–1)= –4.96 kJ•mol^-1
b. U = 1/ε (qiqj/rijÅ) x 1390 kJ•mol^(–1)
U = 1/2(-1/3.5) x 1390 kJ•mol^(–1)= –199 kJ•mol^-1

7.1) It is easier to predict the bulk behavior of a small
number of molecules than a large number of molecules. (True/False)

False

7.3) Consider a coin with two sides (H = heads; T = tails). The
probability of observing HHHHHTTTTT is equal to the
probability of observing HTHTHTHTHT.
(True/False)

True

7.7) A state corresponds to many different microstates. (True/False)

True

7.9) When the volume of a system increases, its multiplicity
________.

increases

7.11) The combined entropy of the system and surroundings
always _______________ for a spontaneous process.

increases

7.13) A coin is weighted deliberately so that the probability
of tossing heads is twice the probability of tossing tails.
What is the probability of tossing three heads in a row?
What is the probability of tossing three tails in a row?
What is the relative probability of tossing three heads
versus three tails?

increases
2/3 chance of heads, 1/3 of tails.
3 heads in a row = (2/3)3 = 8/27 = 0.296.
3 tails in a row = (1/3)3 = 1/27 = 0.037.
Relative probability = (8/27)/(1/27) = 8 times more likely

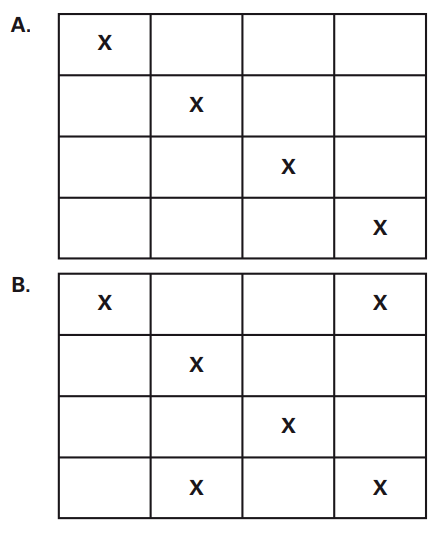
7.17) Consider the systems below consisting of different
numbers of identical molecules (indicated by the
symbol X) and equal-sized grid boxes that are either
empty or occupied by a molecule. Which system has
a higher entropy? What is the difference in entropy
between A and B?

WA = 16!/12!4!
WB = 16!/6!10!
WB > WA

7.20) System A has a multiplicity of 15, whereas System B has
a multiplicity of 12. What is the total entropy of Systems
A and B?

The entropies of the two parts will be additive.
Therefore we can calculate them separately.
SA = kB ln(15) = 2.71 kB; SB = kB ln(12) = 2.48 kB.
Total entropy = 5.19 kB.

8.2) If the second-lowest energy level is separated from the
ground state by 0.5kBT, then the second-lowest energy
level will not be occupied appreciably. (True/False)

False

8.6) After spontaneous heat transfer between systems, the
overall multiplicity is:
a. lower than it was before the transfer of heat
b. zero
c. maximized
d. minimized

C

8.8) The Boltzmann distribution describes the energy of
molecules at _________________.

equilibrium

8.10) Kinetic energy is due to the __________ of atoms.
Potential energy is due to the ___________ of atoms.

motion, configuration/relative positions

8.12) If two systems of different temperatures are brought
together, there will be a net transfer of heat from the
system of __________ temperature to the system of
_________ temperature.

higher, lower

8.14) A system starts with a multiplicity of 1099. Heat is transferred out of the system reversibly at 298 K such that
the final multiplicity is 105. How much heat was lost?

∆S = kB ln(Wfinal/Winitial) = kB ln (10^5/10^99) = -216J*K^-1
qrev = T∆S = (298 K)(–216 J•K^–1) = -64.5 kJ
64.5 kJ of heat are lost

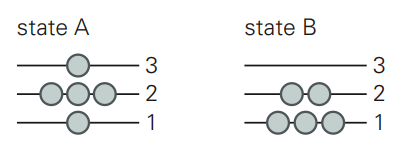
8.17) Consider a system with five molecules and three energy
levels. The energy levels are such that a molecule at
energy level 1 contributes 1 J of energy to UTOTAL, a
molecule at energy level 2 contributes 2 J of energy to
UTOTAL, and a molecule in energy level 3 contributes
3 J of energy to UTOTAL. Which has more internal energy,
state A or state B?

For State A
UTOTAL = ΣNiUi = 3 × N3 + 2 × N2 + 1 × N1
= 3 × 1 + 2 × 3 + 1 × 1 = 10
For State B
UTOTAL = ΣNiUi = 3 × N3 + 2 × N2 + 1 × N1
= 3 × 0 + 2 × 2 + 1 × 3 = 7
Therefore, system A has greater energy.

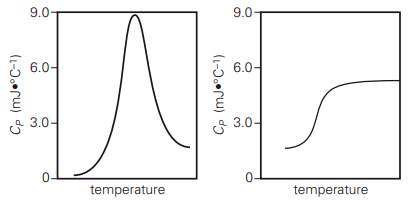
6.20) Below are two graphs of heat capacity changes in
a differential scanning calorimeter experiment. In
the experiment, protein molecules in solution are
unfolded by increasing the temperature. In both graphs,
temperature increases from left to right. Which graph
correctly characterizes the heat capacity changes of
a protein as it is heated? Which characteristics in the
graph lead to this conclusion?

The graph on the left is correct. Both graphs correctly
indicate that the heat capacity at low temperatures,
when the protein is folded, is lower than the heat
capacity at high temperatures, when the protein is
unfolded. However, the heat capacity of a protein peaks
at its melting temperature because relatively more
energy goes into breaking intramolecular interactions.
It then decreases at higher temperatures when fewer
unbroken interactions persist. Only the left graph
indicates this correctly.