INTECH 1100 REVIEWERR
5.0(2)
Card Sorting
1/74
Earn XP
Description and Tags
Last updated 12:53 PM on 11/28/22
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No analytics yet
Send a link to your students to track their progress
75 Terms
1
New cards
The study of discrete, mathematical objects and Structures.
DISCRETE MATHEMATICS
2
New cards
defined as the study of correct reasoning.
Logic
3
New cards
allows you to give a temporary name to what you are seeking so that you can perform concrete computations with it to help discover its possible values.
variable
4
New cards
3 types of statement
universal, conditional, existential
5
New cards
certain property is true FOR ALL elements in a set.
Universal Statement
6
New cards
IF one thing is true THEN some other things also has to be true
Conditional Statement
7
New cards
THERE IS at least one thing for the property is true.
Existential Statement
8
New cards
a statement that is both universal and conditional.
universal conditional statement
9
New cards
first part says that a certain property is true for all objects of a given type, and it is existential because its second part asserts the existence of something.
EXAMPLE: For all real numbers r, there is an additive inverse for r.
EXAMPLE: For all real numbers r, there is an additive inverse for r.
universal existential statement
10
New cards
a statement that is existential because its first part asserts that a certain object exists and is universal because its second part says that the object satisfies a certain property for all things of a certain kind.
EXAMPLE: There is a positive integer that is less than or equal to every positive integer.
EXAMPLE: There is a positive integer that is less than or equal to every positive integer.
Existential Universal Statement
11
New cards
The central concept of deductive logic is the concept of argument form. An argument is a sequence of statements aimed at demonstrating the truth of an assertion.
Logical Form and Logical Equivalence
12
New cards
The assertion at the end of the sequence.
Conclusion
13
New cards
Also known as proposition - it is a sentence that is true or false but not both.
Statement
14
New cards
what is the meaning of this symbol ~
NOT
15
New cards
what is the meaning of this symbol Ʌ
And
16
New cards
what is the meaning of this symbol V
Or
17
New cards
symbol of Negation of p
“~p”
18
New cards
symbol of Conjunction of p and q .
“p Ʌ q”
19
New cards
symbol Disjunction of p and q.
“p V q”
20
New cards
a breakdown of a logic function by listing all possible values the function can attain.
Truth Values
21
New cards
an expression made up of statement variables (such as p, q, and r) and logical connectives (such as ~p, Ʌ, and V) that becomes a statement when actual statements are substituted for the component statement variables.
statement form (or propositional form)
22
New cards
Two statement forms are called _______if, and only if, they have identical truth values for each possible substitution of statements for their statement variables.
Logical Equivalence
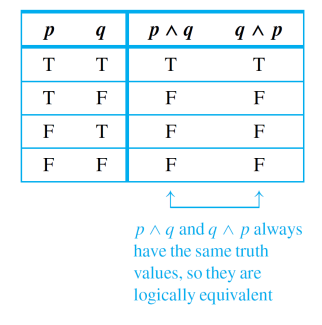
23
New cards
The negation of an and statement is logically equivalent to the or statement
The negation of an or statement is logically equivalent to the and statement
The negation of an or statement is logically equivalent to the and statement
De Morgan’s laws

24
New cards
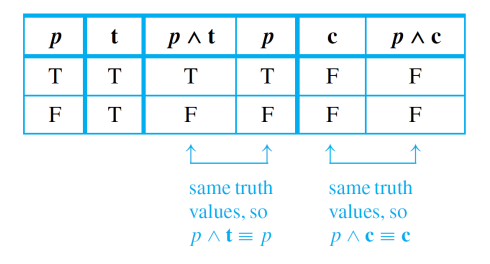
is a statement form that is always true
Tautology
25
New cards
Contradiction
is a statement form that is always false
26
New cards
A _____ is a statement that can be written in the form “If P then Q,” where P and Q are sentences.
conditional statement
27
New cards
the symbol"→ " means
if then
28
New cards
In a symbol "p → q”. p is ____ and q is _____?
p is called the hypothesis
q is called the conclusion.
q is called the conclusion.
29
New cards
in and "if-then" statement it will get false when the hypothesis is ___ and the conclusion is ___
hypothesis (p) is true and conclusion (q) is false
30
New cards
the symbol for" Negation of a Conditional
Statement"
Statement"
The negation of "if p then q" is logically equivalent to "p and not q
- Remove the if and then in a statement and negate the (q)
- Remove the if and then in a statement and negate the (q)
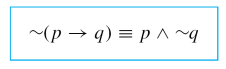
31
New cards
______ is logically equivalent to its contrapositive.
Conditional statement
32
New cards
what do you call to this kind of statement?
∼q →p
∼q →p
Contrapositive of a Conditional Statement
33
New cards
what do you call to this kind of statement?
"If q then p”
q → p,
"If q then p”
q → p,
converse
34
New cards
what do you call to this kind of statement?
"If ∼p then ∼q”
∼p → ∼q
"If ∼p then ∼q”
∼p → ∼q
inverse
35
New cards
A conditional statement and its converse are ?
not logically equivalent.
36
New cards
A conditional statement and its inverse?
not logically equivalent.
37
New cards
The converse and the inverse of a conditional statement ?
logically equivalent to each other.
38
New cards
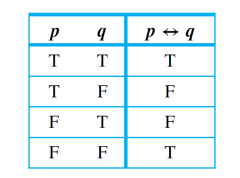
↔ is a symbol of?
IF and ONLY IF
39
New cards
a sequence of statements ending in a conclusion.
Argument
40
New cards
is a sequence of statement forms
Argument form
41
New cards
statements in an argument and all statement forms in an argument form, except for the final one and this called?
premises (or assumptions or hypotheses).
42
New cards
The final statement or statement form is called the?
conclusion
43
New cards
An argument form is called valid when both premise and conclusion is?
true
44
New cards
the symbol" •" which is read as?
therefore
45
New cards
A row of the truth table in which all the premises are true
critical row
46
New cards
a logical form or guide consisting of premises (or hypotheses) and draws a conclusion
rule of inference
47
New cards
An argument form consisting of two premises and a
conclusion
conclusion
modus ponens
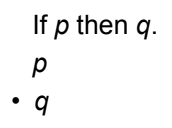
48
New cards
Modus Tollens
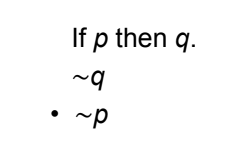
49
New cards
Generalization
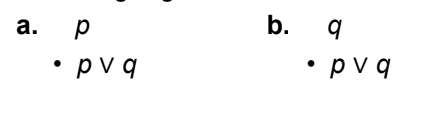
50
New cards
specialization

51
New cards
Elimination

52
New cards
Transitivity
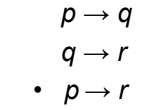
53
New cards
Proof by Division into Cases
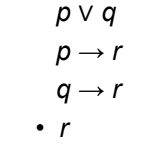
54
New cards
a sentence with variables that becomes a statement when specific values are substituted for the variables.
Predicate
55
New cards
a predicate variable is the set of all values that may be substituted in place of the variable.
Domain
56
New cards
Some ways to express the symbol ∀ in words are ______.
for all, for any.
57
New cards
Some ways to express the symbol ∃ in words are ______.
there exists, at least one.
58
New cards
A statement of the form ∀x ∈ D, Q(x) is true if, and only if,Q(x)is __________ for ______ .
A statement of the form ∀x ∈ D, Q(x) is true if, and only if,Q(x) is true for every x in D.
59
New cards
A statement of the form ∃x ∈ D such that Q(x) is true if, and only if, Q(x) is ______ for _____.
A statement of the form ∃x ∈ D such that Q(x) is true if, and only if, Q(x) is true for at least one x in D.
60
New cards
Let Q(n) be the predicate "n is a factor of 8." Find the truth set of Q(n) if the domain of n is the set Z+ of all positive integers
The truth set is {1,2,4,8} because these are exactly the positive integers that divide 8 evenly.
61
New cards
Let Q(n) be the predicate "n is a factor of 8." Find the truth set of Q(n) if the domain of n is the set Z of all integers.
The truth set is {1,2,4,8,−1,−2,−4,−8} because the negative integers −1,−2,−4, and −8 also divide into 8 without leaving a remainder.
62
New cards
Convert "All human beings are mortal" using universal quantifiers.
∀ human beings x , x is mortal.
63
New cards
Convert "For all x in the set of all human beings, x is mortal" using universal quantifiers.
∀x ∈ H, x is mortal
64
New cards
Rewrite the following statement using an equivalent non formal definition:
∀x∈R, x^2 ≥0
∀x∈R, x^2 ≥0
All real numbers have nonnegative squares.
65
New cards
Rewrite the following statement using an equivalent non formal definition:
∀x∈R,x^2 does not equal -1
∀x∈R,x^2 does not equal -1
All real numbers have squares that do not equal -1.
66
New cards
Rewrite the following statement using an equivalent non formal definition:
∃m ∈ Z+ such that m^2 = m
∃m ∈ Z+ such that m^2 = m
There is a positive integer whose square is equal to itself.
67
New cards
Rewrite the statement formally. Use quantifiers and variables.
All triangles have three sides.
All triangles have three sides.
∀ triangles t , t has three sides.
68
New cards
Rewrite the statement formally. Use quantifiers and variables.
No dogs have wings.
No dogs have wings.
∀ dogs d, d does not have wings.
69
New cards
Rewrite the statement formally. Use quantifiers and variables.
Some programs are structured.
Some programs are structured.
∃ a program p such that p is structured.
70
New cards
Rewrite the following statement informally, without quantifiers or variables.
∀x∈R, if x>2 then x^2 >4.
∀x∈R, if x>2 then x^2 >4.
For all real numbers x, if x is greater than 2 its square is greater than 4.
71
New cards
Rewrite each of the following statements in the form
∀ ________, if ______ then _____ .
If a real number is an integer, then it is a rational number.
∀ ________, if ______ then _____ .
If a real number is an integer, then it is a rational number.
∀ real numbers x, if x is an integer then x is a rational number.
72
New cards
Rewrite each of the following statements in the form
∀ ________, if ______ then _____ .
All bytes have eight bits.
∀ ________, if ______ then _____ .
All bytes have eight bits.
∀ x, if x is a byte then x has 8 bits.
73
New cards
Rewrite each of the following statements in the form
∀ ________, if ______ then _____ .
No fire trucks are green.
∀ ________, if ______ then _____ .
No fire trucks are green.
∀ x, if x is a firetruck then x is not green.
74
New cards
Rewrite the following statement in the two forms, all squares are rectangles.:
"∀x, if _____ then ______" and
"∀ _______ x, ______":
"∀x, if _____ then ______" and
"∀ _______ x, ______":
∀x, if x is a square then it is a rectangle.
∀ squares x, x is a rectangle.
∀ squares x, x is a rectangle.
75
New cards
Indicate which of the following statements are true and which are false. Justify your answers as best as you can.
a. Every integer is a real number.
b. 0 is a positive real number.
c. For all real numbers r, −r is a negative real number.
d. Every real number is an integer.
a. Every integer is a real number.
b. 0 is a positive real number.
c. For all real numbers r, −r is a negative real number.
d. Every real number is an integer.
a. True, the statement is true. The integers correspond to certain points on the number line and the real numbers correspond to all the points on the number line.
b. False, 0 is neither positive or negative.
c. False, since - (-2) equals a positive 2.
d. False, for instance 1/2 is a real number but not an integer.
b. False, 0 is neither positive or negative.
c. False, since - (-2) equals a positive 2.
d. False, for instance 1/2 is a real number but not an integer.