geometry theorems/postulates

proof stuff basically

conjecture

a hypothesis is based upon observations from the postulates. Not yet set in stone.

theorem

A theorem is a proposition that has been or is to be proved by the use of logic on the basis of explicit assumptions (use converse when proving opposite)

postulate

basic assumptions of geometry

segment additon postulate (SAP)

if point B is on AC and is between points A and C then AB + BC = AC

angle addition postulate (AAP)

if point D lies in the interior of <ABC then m<ABD + m<DBC = m<ABC

linear pair postulate (LPP)

if two angles form a linear pair then the angles are supplementary

corresponding angles postulate (CAP)

if two parallel lines are cut by a transversal then corresponding angles are congruent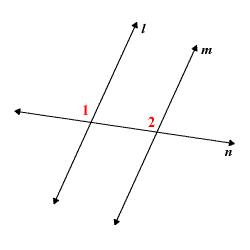

SSS Postulate

If 3 sides of one triangle are congruent and corresponding to 3 sides of another triangle then the 2 triangles are congruent

SAS Postulate

If 2 sides and an included angle in 1 triangle are congruent and corresponding to another triangle then the triangles are congruent

ASA Postulate

If 2 angles are congruent and the included side

reflexive property

when something is congruent/equals itself

substitution property

when you substitute something in the equation

transitive property

when something both equals to one thing so they equal each other

combining like terms (CLT)

when you simplify the equation by combining things

symmetric property

if x = y , then y = x

commutative property

a+b = b+a

associative property

(a+b) + c = a + (b+c)

Distributive Property

a(b+c) = ab + ac

Definition of Congruent Segments (DOCS)

definition of congruent angles (DOCA)

changes from congruent to equal or vice versa

definition of perpendicular lines

lines/segments that intersect to form right angles

definition of a midpoint

point on a line segment that divides it into 2 congruent parts

definition of an angle bisector

a ray that divides an angle into 2 congruent angles

definition of supplementary angles (DOSA)

a pair of angles whose measures add up to 180

vertical angle theorem (VAT)

if two lines intersect and form a pair of vertical angles then the vertical angles are congruent

midpoint theorem

if M is the midpoint of AB then AM = ½ AB

overlapping segments theorem

If AD has points A, B, C, and D in that order with AB congruent to CD , then the overlapping segments AC and BD are congruent.

Overlapping angles theorem

If two parts of an angle are congruent and there is an overlap then both overlaps are congruent.

Alternate Interior Angles Theorem (AIAT)

If two parallel lines are cut by a transversal then alternate interior angles are congruent

Alternate Exterior Angles Theorem (AEAT)

If two parallel lines are cut by a transversal then alternate exterior angles are congruent

Same Side Interior Angles Theorem (SSIAT)

If two parallel lines are cut by a transversal then same side interior angles are supplementary

Same Side Exterior Angles Theorem (SSEAT)

If two parallel lines are cut by a transversal then same side exterior angles are supplementary

Triangle Sum Theorem (TST)

all angles in a triangle add up to 180 degrees

Isosceles Triangle Theorem (ITT)

If two side of a triangle are congruent then its base angles are congruent

Triangle Inequality Theorem

the sum of the lengths of any two side of a triangle is greater than the length of the 3rd side

Side Angle Inequality Theorem

if one side of a triangle is longer than other side the angle opposite the longer side is larger than the angle opposite the shorter side

Triangle Exterior Angle Theorem

the measure of an exterior angle of a triangle is equal to the sum of the measures of its remote interior angles

Perpendicular Bisector Theorem (there is a converse)

if a point is on the perpendicular bisector of a segment then it is equidistant from the endpoints

Shortest Distance Theorem

the shortest distance from a point to a line is measured along the altitude from the point to the line.

SAA Theorem

If two angle sand a non-included side of one triangle are congruent to the corresponding two angles and non-included side of another triangle then the triangles are congruent

Hypotenuse Leg Theorem (HL Theorem)

If the hypotenuse and a leg of one right triangle are corresponding and congruent to another hypotenuse and a leg of another right triangle, then the two triangles are congruent.

Vertex Angle Bisector Theorem (has a converse)

in an isosceles triangle, the bisector of the vertex angle is also the median and the altitude

Equilateral/Equiangular Triangle Theorem:

every equilateral triangle is equiangular and conversely every equiangular triangle is equilateral

Angle Bisector Theorem

If a point is on the bisector of an angle then it is equidistant from the sides of the angle

Triangle Proportionality Theorem:

If a line parallel to the one side of a triangle it divides the other two sides proportionally

CPCTC:

Corresponding Parts of Congruent Triangles Are Congruent