psychometrics

factor matrix

correlations (factor loadings) of the items with the factors of the unrotated factor solution

before rotation all items load as high as possible on the first factor, because the first factor explains the most variance.

pattern matrix

semi-partial correlations ritem1,factor1.factor2 (comparable to regression coefficients) of the items and the factors of the rotated factor solution.

Often called the unique contribution of a factor to an item

usually the most clear structure

factor correlation matrix

shows the correlation between the factors for the rotated solution

this correlation is 0 per definition if we use varimax (orthogonal) rotation

structure matrix

e correlations between the items and the factors of the rotated factor solution

unidimensional test

includes items that reflect only a single attribute of a person

Only a single score is computed

all the items are combined into a compositive score

conceptual homogeneity

responses to each item are a function of the same psychological attribute

multidimensional tests

can produce a variety of scores

each subtest is unidimensional and has its own score

whole test can be scored in several ways; second order structure is the most common

explorative factor analysis

tries to identify sets of items that strongly correlate with each other and weakly correlate with others

orthogonal rotation

generates factors that are uncorrelated with each other

varimax is the most common

obique rotation

generates factors that are either correlated or uncorrelated with each other

allows the factors to do what they want

→ preferred by experts

factor loading in orthogonal rotation

loadings can be seen as correlation between each item and each factor

pattern coefficient

reflect the unique association between an item and a factor

structure coefficient

correlations between respondents item responses and their levels of the underlying factor

interpreting factor loadings

1. size of loading indicated the degree of association between an item and a factor → larger loading means larger association

2. direction of loading: positive loading means that people with a high score have high levels of the underlying factor

simple structure

occurs when each item is strongly associated with only one factor

validity

not the property of a test, is related to interpretation and use of the scores in a specific context

is a matter of degree

is based on strong empirical evidence

construct validity

considered the essential concept of validity

validity definition

the degree to which evidence and theory support the interpretations of test scores for proposed uses

facets of construct validity

• test content (content validity)

• internal structure (structural validity)

• response processes (response process validity)

• association with other variables (associative validity)

• consequence of use ( consequential validity)

content validity

is rated by experts

does the content of the test match what should be in the test

threats to content validity

Construct irrelevant content

Construct underrepresentation

face validity

the degree to which a test appears to be related to a specific construct

weakest form of validity, but influences participant motivation

structural validity

Does the internal structure of the test match the internal structure the test should have

evidence through factor analysis (number of factors, association among factors, meaning of factors)

response process validity

Do the psychological processes that respondents use when completing a measure match the processes they should use?

evidence comes from interviews and indirect indicators like response time and eye tracking

associative validity

Do the associations between the test and other measures match the associations the test should have with these other measures?

relevant evidence: correlations

• convergent validity

• discriminant validity

• concurrent and predictive validity (criterion validity)

consequential validity

Do the consequences of using a test match the consequences that should be seen?

Are the test scores equally valid for different groups?

relevant evidence: evaluation of intended consequences, unintended differential impact and systematic changes

reliability

the extent to which differences in respondents' observed scores are consistent with differences in their true score

is a property of test responses and test scores (consistency)

effects of reliability

affects the association between variables, which is an aspect of construct validity (associative validity)

we can use correlations to make conclusions about validity

high reliability is necessary for validity but not sufficient

convergent validity

Are variables that should be (highly) positively correlated, actually (highly) positively correlated?

Are variables that should be (highly) negatively correlated, actually (highly) negatively correlated?

discriminant validity

Are variables that should not be correlated, actually uncorrelated?

multitrait-multimethod matrices

purpose: to set clear guidelines for evaluating convergent and discriminant validity

evaluate construct/trait variance and method variance

construct/trait variance

Tests share _________ when they measure the same (or similar) constructs

method variance

share ________ when they use the same type of measure/instrument (e.g., self-reports on both measures, parents filling out both questionnaires)

outcomes multitrait-multimethod matrices

same trait - same method: reliabilities should be high because they affect the observed correlation between variables

same trait - different method: correlation should be moderate to high because it measures the same construct

different trait - same method - correlation depends on the constructs you are measuring and the expectations should be based on theory

different trait - different method: also depends on the measured construct but should be lower than the one with same method; weakest correlation

sources of variance

systematic

• trait/construct → intended

• method → variance in the scores caused by the instrument used (unintended)

• subject properties: variance that comes from differences between participants that are not related to the measured trait (unintended)

• situation/location: variance comes from differences in the environment or context in which a measurement takes place (unintended)

  unsystematic

• measurement error

validity coefficient

is a correlation

can be inflated by unintended systematic variances, are not accurate

factors affecting a validity coefficient

association between constructs: the higher the association the higher the coefficient

measurement error and reliability: the validity coefficient is affected by the reliability of the test and criterion

restricted range: causes weaker correlation

skew and relative proportions: differential skew→ weaker possible correlation

time: greater distance → weaker correlation

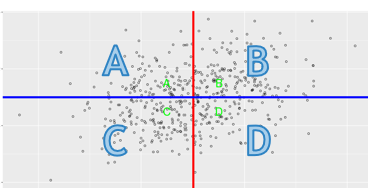
sensitivity

the proportion of people who meet the criterion, and who are correctly identified by the test

B/ A+B

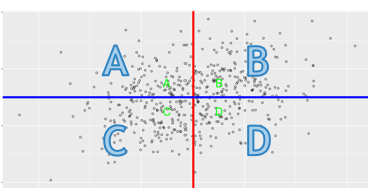
specificity

the proportion of people who do not meet the criterion, and who are correctly identified by the test

C/C+D

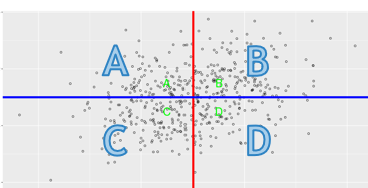
positive predictive value (success rate)

the probability that someone with a positive test result actually meet the criterion

B/B+D

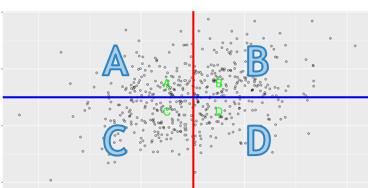
negative predictive value

the probability that someone with a negative test result actually does not meet the criteria

C/A+C

base rate

everyone who actually meets the criterion

test rate

proportion of people who were identified by the test

reliability depends on what

1. the extend to which differences in test scores can be attributed to real differences

2. the extend to which differences in test scores are a function of measurement error

key assumptions of reliability

1. a persons observed score on a test is a function of that persons true score, plus error

2. measurement error is random → it cancels itself our across respondents and they are uncorrelated with true scores

variance of error scores

represents the degree to which error affects different people in different ways

→ high error variance indicates the potential for poor measurement

four ways to think about reliability

1. as the ratio of true score variance to observed score variance

2. as lack of error variance

3. as the squared correlation between observed scores and true scores

4. as the lack of squared correlation between observed scores and error scores

standard error of measurement

represents the average size of error scores

larger means greater difference between true and observed score and less reliability

assumption that error is random

1. respondents true score on each test are uncorrelated with their error scores on the other tests

2. respondents error score on test 1 are uncorrelated with error scores on test 2

common assumptions among all models

error is random

tests are unidimensional

true scores on one test are linearly related to the true scores on other tests

differences in assumptions of models

slope value

intercept value

same error variance

parallel tests criteria

basic assumptions of CTT are met

3 additional assumptions

1. slope for true scores is one

2. intercept for true scores is 0

3. two tests have the same error variance

→ correlation between parallel tests is equal to the reliability

implications of same error variance

1. perfect correlation of true scores

2. identical mean true score across tests

3. identical variability

4. identical mean observed scores

5. identical variability of observed scores

tau-equivalence criteria and implications

all basic CTT assumptions are met

2 additional assumptions

1. intercept for true scores is 0

2. slope for true scores is 1

perfect correlation of true scores

identical variability of true scores

identical mean true scores across tests

identical mean of observed scores

essentially tau-equivalent criteria and implications

CTT assumptions are met

slope for true scores is 1

perfect correlation of true scores

identical variability of true scores

basics of the methods for estimating reliability

• no single method can provide a completely accurate estimate

• every method requires at least two testing’s to generate an estimate of reliability

• consistency is the basis of estimating reliability for every method

alternate forms method of estimating reliability

• obtain scores from two different test forms and compute the correlation between the two forms

• take that as an estimator of reliability

• only works when test forms are parallel

disadvantages of alternate forms method of estimating reliability

we can never know if two tests are parallel

there is potential for carryover effect or contamination due to repeated testing

contamination

error on one test might influence the error on another test but according to CTT it must be random

assumed parallel items

when we have two test forms that have similar means and standard deviations and we feel confident that they measure the same construct

test-retest method of estimating reliability

requires the people to take the same test one more than one occasion

is assumptions are met then the correlation between test and retest can be interpreted as an estimate of the test reliability

assumes that the two test occasions produce test scores that are equally reliable

disadvantages of test-retest method of estimating reliability

stability assumptions

error variance is strongly affected by temporal elements so test situations have to be set up carefully because we need error variance to be the same

we assume same true scores → respondents might experience psychological changes between occasions which change their true score

length of interval has an effect

short intervals carry the risk of contamination/carryover

long intervals make psychological changes more likely

psychological changes are more likely in certain lifetime periods

internal consistency method of estimating reliability

requires only one test

different parts of a test can be treated as different forms of a test

if the different parts are highly correlated it is likely that the test is reliable

long test is likely to provide more reliable sources

split-half reliability

sort the test items into two parallel subtests of equal size

compute a score for each subtest and correlate those

enter the correlation in a formular

→ idea is to create tow parallel subtests

raw coefficient alpha

is an item level approach, conceives of every item as a subtest

consistency among all of the items can be used to estimate the reliability

Cronbachs alpha (raw alpha)

most widely used method

calculate the variance of scores on the complete test

calculate the covariance between each pair of items

sum up covariances → larger sum means items are more consistent

enter into equation

obtaining a negative alpha

may be because something is very wrong with the test

the test is fine but more items need to be reverse scored

standardized coefficient alpha (spearman brown formular)

highly related to raw alpha

is appropriate when test items are scored on different scales and therefore have dramatically different variances

1. obtain a set of item level statistics

2. calculate the correlations between each pair of items

3. average pairwise correlations

4. enter in the equation

Raw alpha for binary items (KR-20)

is algebraically identically to raw alpha

for each item calculate the proportion of each of the two possible answers

calculate the variance for each item and the variance of the total test score

enter into the formular

factors affecting the reliability of test scores

1. consistency among the parts of a test

2. length of the test → as test length increases, true score variance increases more than error variance

3. sample heterogeneity and reliability generalization

spearman brown prophecy formular

estimates the reliability of a revised test

can be used to forecast what would happen if a test was revised in a particular way

length only improves reliability if everything else stays the same

items must be parallel

intraindividual change score

each person has two scores on the same test of measure

intraindividual discrepancy score

each person has scores from two different test

estimating reliability of difference scores

estimation on the basis of three sets of information

1. the estimated reliability of each set of test scores used to compute the difference scores

2. variability of the tests observed scores

3. correlation between observed test scores

factors affecting the reliability of difference scores

1. correlation of observed scores → is two tests have high correlation, the difference score has low reliability

2. reliability of the two test scores used to compute the difference scores → positive correlation

reliability of the difference scores will not be higher than the average reliability of the two test scores but can be much lower

problems of unequal variability

if tests have different variability, the difference score will be strongly linked to the test with the higher variance