4. Fundamentals of Quantum Mechanics

Evidence for wave-nature of particles

Define probability distribution 

Wave particle duality

Classical vs Quantal Descriptions of Nature

Define ψ² and explain its interpretation 

Calculate energy of a particle in a 1D box

How PIB energy changes based on mass, length, and principle quantum number

Define phase of a wavefunction

Define Zero-Point Energy and explain its physical interpretation 

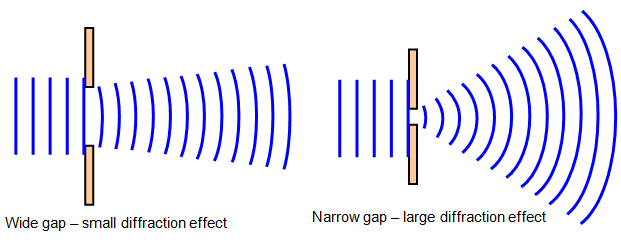
Wave Diffraction

The bending and spreading of waves around obstacles or through openings

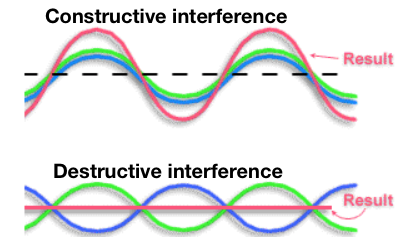
Wave Interference

When two or more waves interact causing the amplitude of the resulting wave to be greater (constructive interference) or smaller (destructive interference) than the individual waves

De Broglie Equation

λ = h/mv

λ = wavelength (m)

h= Planck’s Constant: 6.626×10⁻³⁴

m= Mass of the particle (kg)

V= Velocity of the particle (m/s)

Use: when you need to determine the wavelength of a moving object

Transverse Wave Characteristics

• Amplitude: difference between midpoint and wave crest

• Wavelength: length of one complete cycle

• Frequency: Number of complete cycles per unit time

Speed of Wave Travel

λ = v/f

λ = The wavelength (m)

v= velocity (m/s)

f = frequency (s^-1, Hz)

Nodes

When the oscillation amplitude of a standing wave equals zero. They are areas where the phases change.

Calculating energy of a classic particle in a box

E = (1/2) mv²

The Schrödinger Equation

-(h²/8π²m) (d²Ψ(x)/dx²) + V(x)Ψ(x) = EΨ(x)

Where:

• h= Planck’s Constant: 6.626×10⁻³⁴

• m = the particle mass

• x = the particle position

• V = the potential energY

The Schrödinger Equation For Quantum Particle in a Box

-(h²/8π²m) (d²/dx²)Ψ = EΨ

Complete Wave-function for a Particle in a One-Dimensional Box

Ψn(x) = √(2/L) sin (nπx/L)

Calculating for the Energy of a Particle

En = (h²n²)/8mL²

As the value of n increases, the energy increases. N is restricted to positive integers so there can only be specific values, meaning it’s quantized.

The Ground State

n=1 where there is the lowest possible energy. The lowest energy of a confined quantum particle must always be > than zero. These particles are never at rest.

Zero-Point Energy

The difference between the ground state energy (n=1) and zero.

En = (h²)/8mL²

Excited States

When energy is higher than the ground state. There are infinitely many.

Change of energy between energy levels

ΔE = Ef - Ei = (h²)/8mL² (n²f - n²i)