Circle Theorems and Formulas

Flashcards covering circle theorems, formulas, and relationships including angles, arcs, segment lengths, circumference, area, and the standard equation of a circle.

Central Angle

An angle whose vertex is the center of a circle. The measure of the central angle is equal to the measure of its intercepted arc (m∠ABC = mAC).

Inscribed Angle

An angle whose vertex is on the circle and whose sides contain chords of the circle. The measure of the inscribed angle is half the measure of its intercepted arc: m∠ABC = 1/2 mAC.

Inscribed Quadrilateral

A quadrilateral whose vertices all lie on a circle. Opposite angles are supplementary (add up to 180°): m∠A + m∠C = 180°, m∠B + m∠D = 180°.

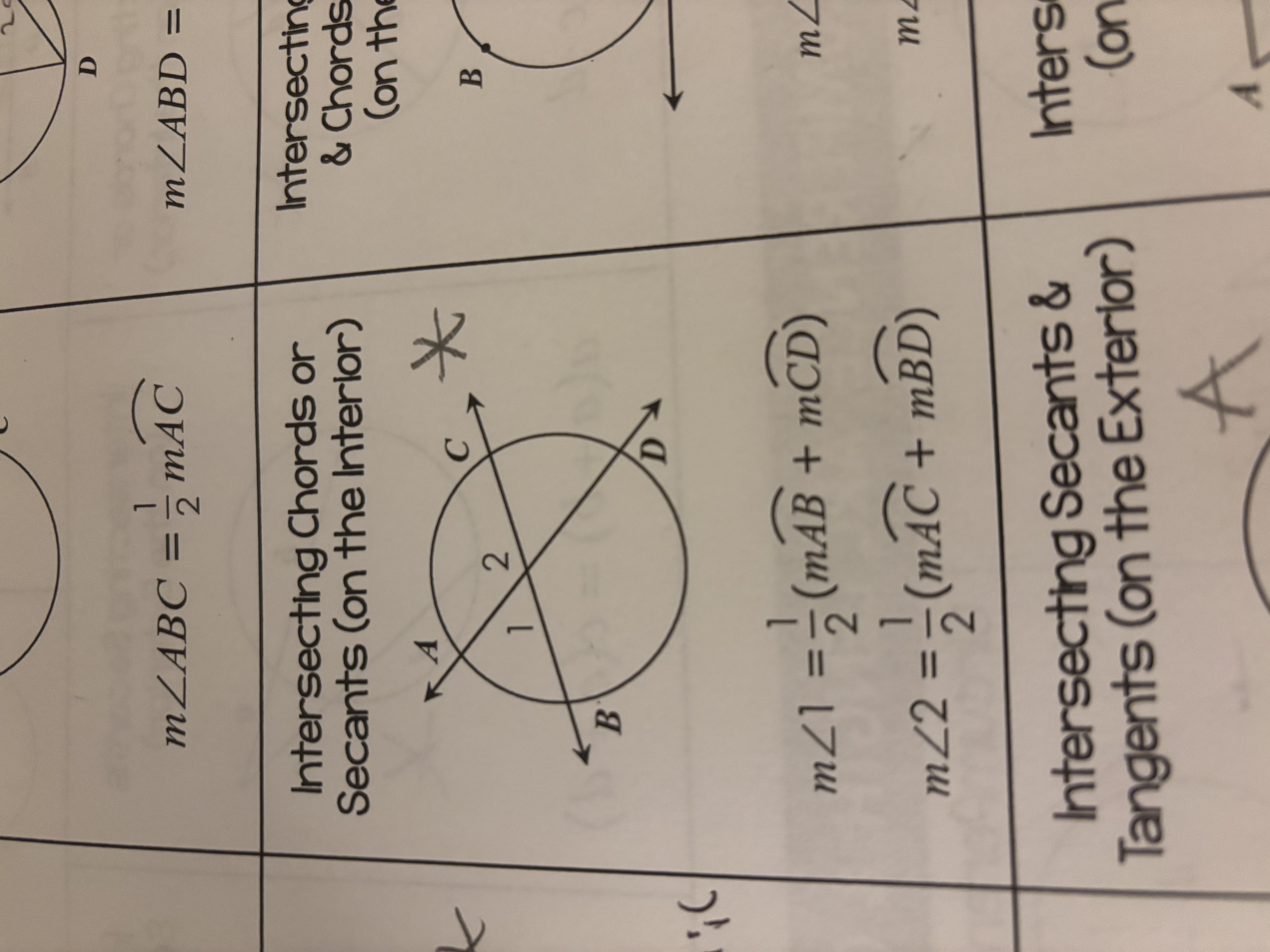
Intersecting Chords or Secants (Interior)

When two chords or secants intersect inside a circle, the measure of the angle formed is half the sum of the measures of the intercepted arcs: m∠2 = 1/2 (mAB + mCD).

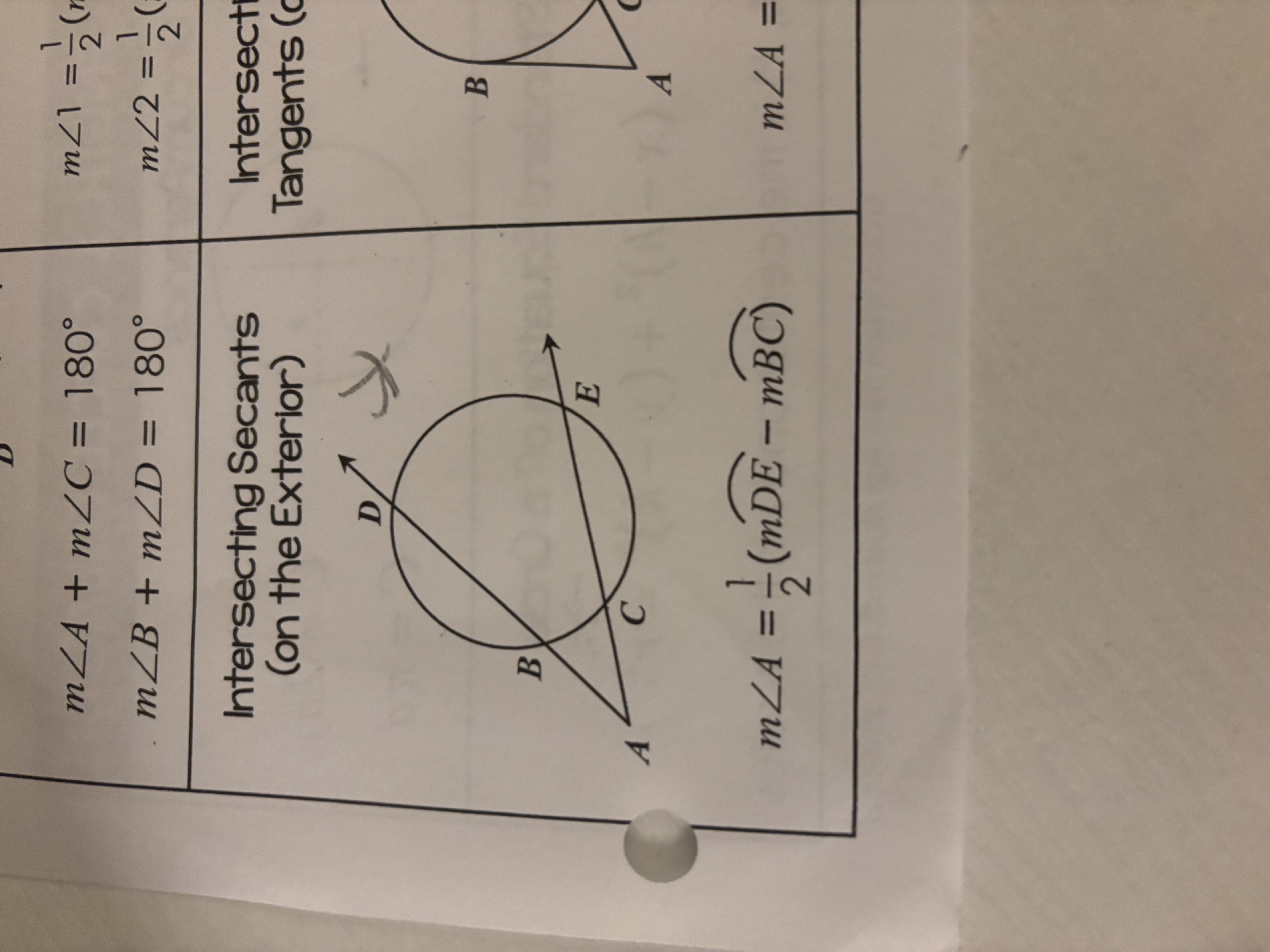
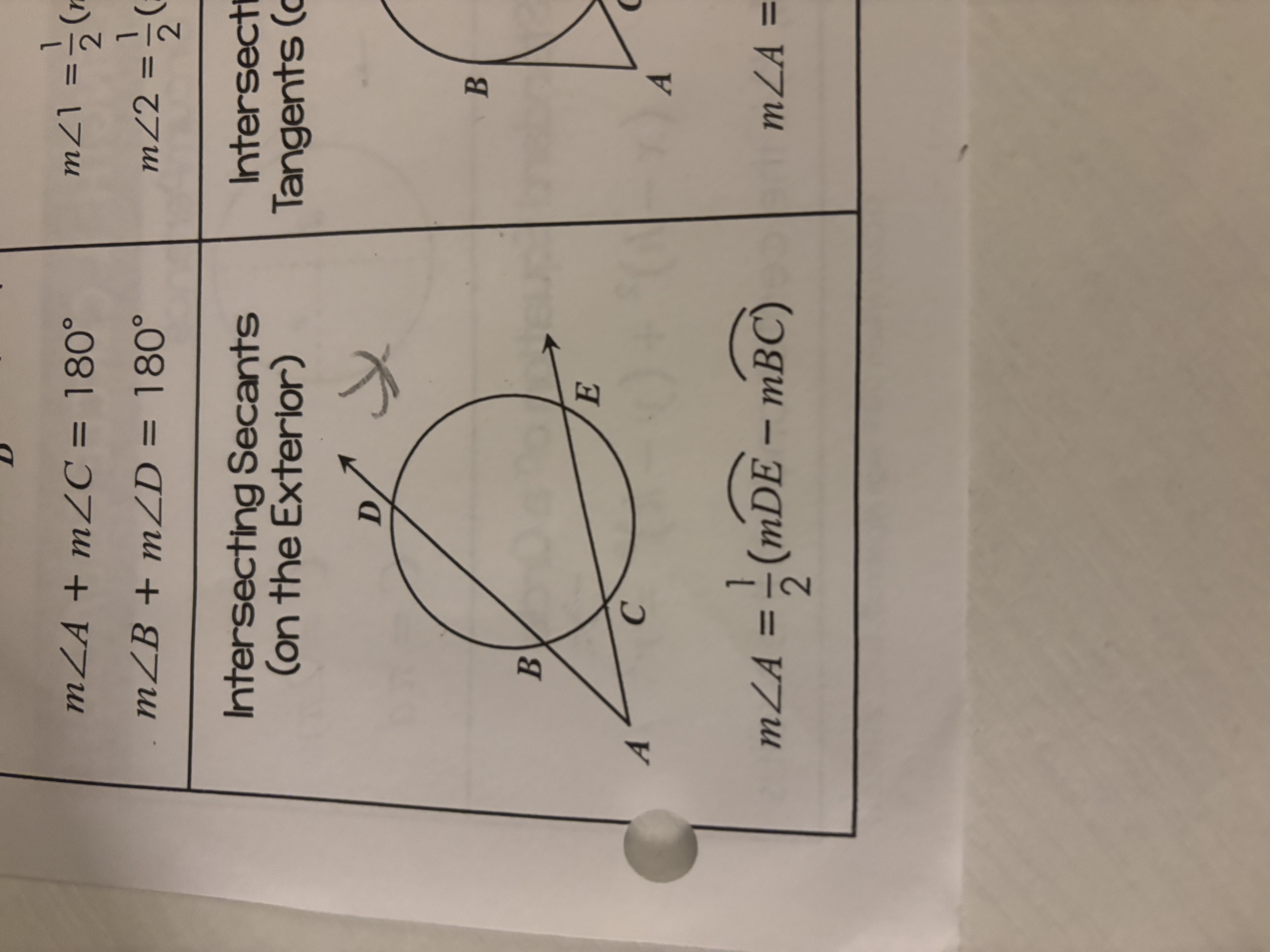
Intersecting Secants (Exterior)

When two secants intersect outside a circle, the measure of the angle formed is half the difference of the measures of the intercepted arcs: m∠A = 1/2 (mBD - mBC).

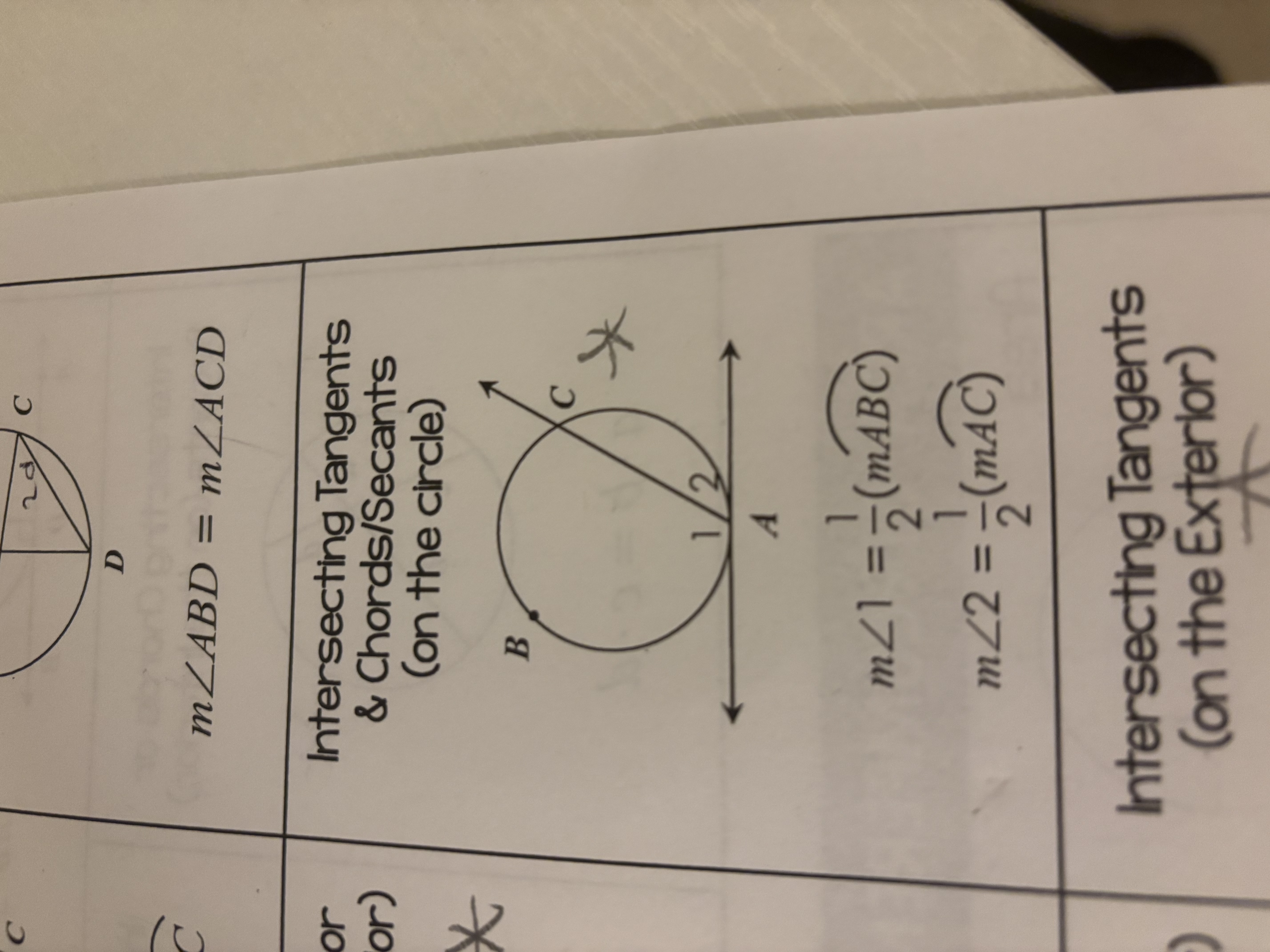
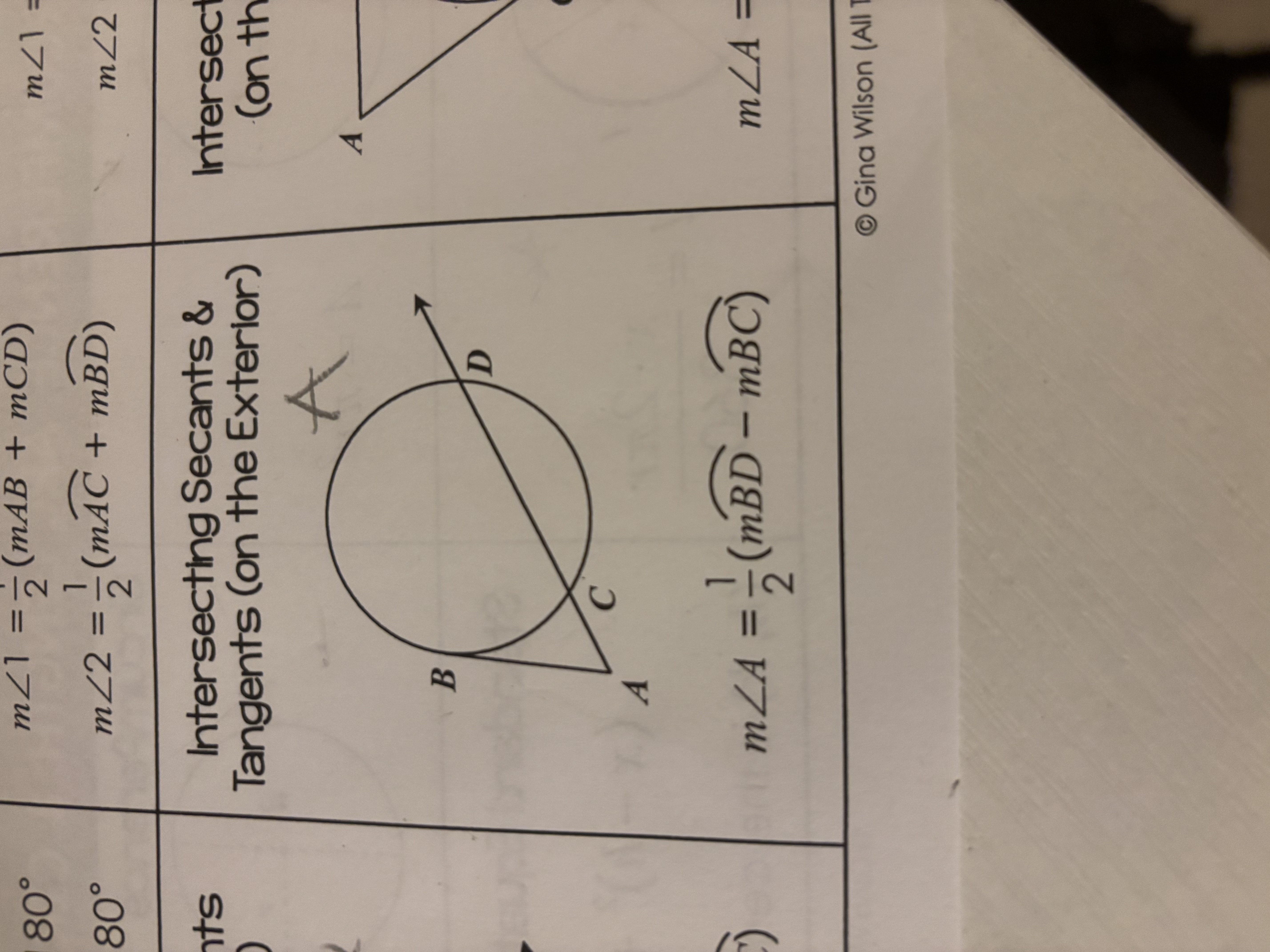
Intersecting Tangents & Chords/Secants (on the circle)

The measure of the angle formed by a tangent and a chord is one-half the measure of the intercepted arc: m∠1 = 1/2 (mABC).

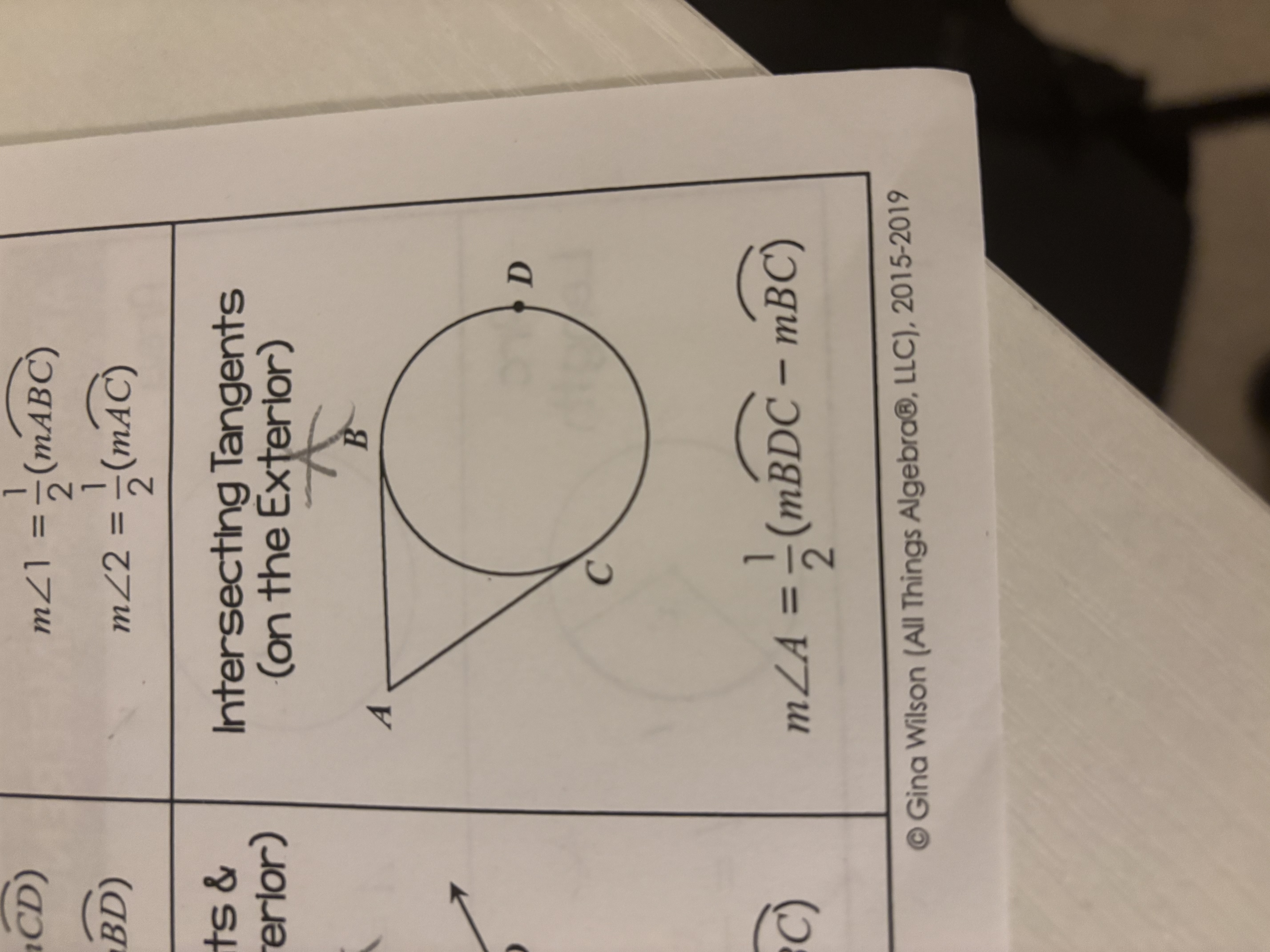
Intersecting Tangents (on the Exterior)

When two tangents intersect outside a circle, the measure of the angle formed is half the difference of the measures of the intercepted arcs: m∠A = 1/2(mBD - mBC).

Tangent to Circle

If a line (AB) is tangent to a circle (C), then the tangent line is perpendicular to the radius (CD) at the point of tangency: AB ⊥ CD.

Two Tangents from External Point

If two tangents (AB and BC) are drawn to a circle (D) from the same external point (B), then the segments are congruent: AB = BC.

Intersecting Chords (Segment Lengths)

When two chords intersect inside a circle, the product of the segments of one chord equals the product of the segments of the other chord: a * b = c * d.

Intersecting Secants (Segment Lengths)

When two secant segments are drawn to a circle from an external point, the product of one secant segment and its external segment equals the product of the other secant segment and its external segment: a(a+b) = c(c+d).

Intersecting Tangent and Secant (Segment Lengths)

When a tangent segment and a secant segment are drawn to a circle from an external point, the square of the tangent segment equals the product of the secant segment and its external segment: a² = b(b+c).

Circumference of a Circle

The distance around a circle, calculated by C = 2πr or C = πd, where r is the radius and d is the diameter.

Area of a Circle

The space occupied within a circle, calculated by A = πr², where r is the radius.

Arc Length

The distance along an arc of a circle, calculated by (x/360) * 2πr, where x is the central angle in degrees and r is the radius.

Standard Equation of a Circle

The equation (x-h)² + (y-k)² = r², where (h, k) is the center of the circle and r is the radius.