Exponentials and Logarithms

0.0(0)
studied byStudied by 2 people
learnLearn
examPractice Test
spaced repetitionSpaced Repetition
heart puzzleMatch
flashcardsFlashcards
Card Sorting

1/7

encourage image

There's no tags or description

Looks like no tags are added yet.

Study Analytics
Name
Mastery
Learn
Test
Matching
Spaced

No study sessions yet.

8 Terms

1
New cards

Derivative of e to the x

y’ = e to the x

<p>y’ = e to the x</p>
2
New cards

Derivative of complex exponential functions

y’ = f’(x) e to the power of f(x)

<p>y’ = f’(x) e to the power of f(x)</p>
3
New cards

Applications of differentiation (exponentials base e)

To find stationary points, solve y’ = 0

To determine concavity, explore whether y’’ > 0 or y’’ < 0

To find points of inflexion y’’ = 0

To find tangents and normals to a curve

<p>To find stationary points, solve y’ = 0 </p><p>To determine concavity, explore whether y’’ &gt; 0 or y’’ &lt; 0 </p><p>To find points of inflexion y’’ = 0 </p><p>To find tangents and normals to a curve </p>
4
New cards

Integration of Exponential Functions and applications of Integration (Standard)

Only works when the index is a linear function

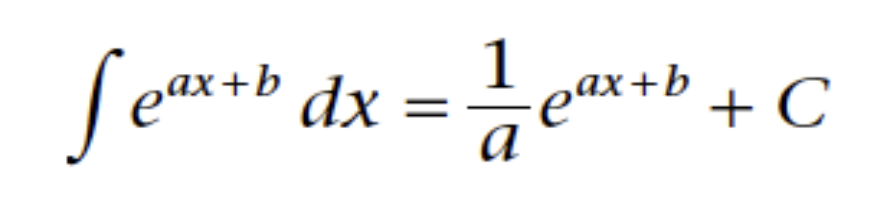
<p>Only works when the index is a linear function</p>
5
New cards

Integration of Exponential Functions and applications of Integration (Reference Sheet)

To remember, it is just the reverse of differentiating exponentials. You may need fudging.

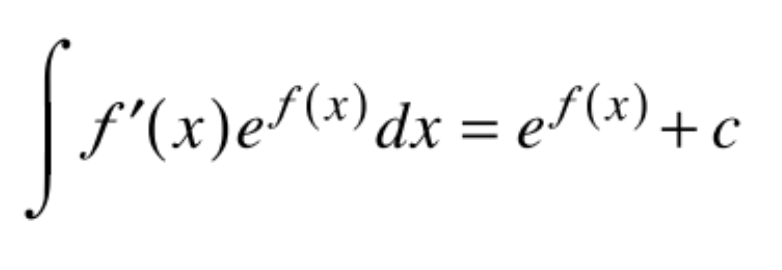
<p>To remember, it is just the reverse of differentiating exponentials. You may need fudging. </p>
6
New cards

Review of Logarithmic Functions

To remember, revise these rules.

<p>To remember, revise these rules.</p>
7
New cards

Derivative of logarithm

Thus why if y = ln(x) y’ = 1/x

<p>Thus why if y = ln(x) y’ = 1/x</p>
8
New cards

Add photos of example question on all of them to assist you in recognition.