A different determinant flashcard set - Matrix Algebra

What does the determinant measure?

How much a linear transformation scales area (2D) or volume (3D).

What does it mean when the determinant = 1?

The transformation preserves are/volume (no growth, no shrink).

What does it mean when the determinant = 0?

It tells us the transformation collapses space into a lower dimension (like a straight line) - the transformation is not invertible.

What about when the determinant > 1?

Space is stretches - area/volume increases.

What about when the determinant is between 0 and 1?

Space is compressed - are/volume decreases.

What about when the Determinant < 0?

Space is flipped (orientation is reversed) in addition to scaling. They invert the orientation of space (like flipping a paper on its backside).

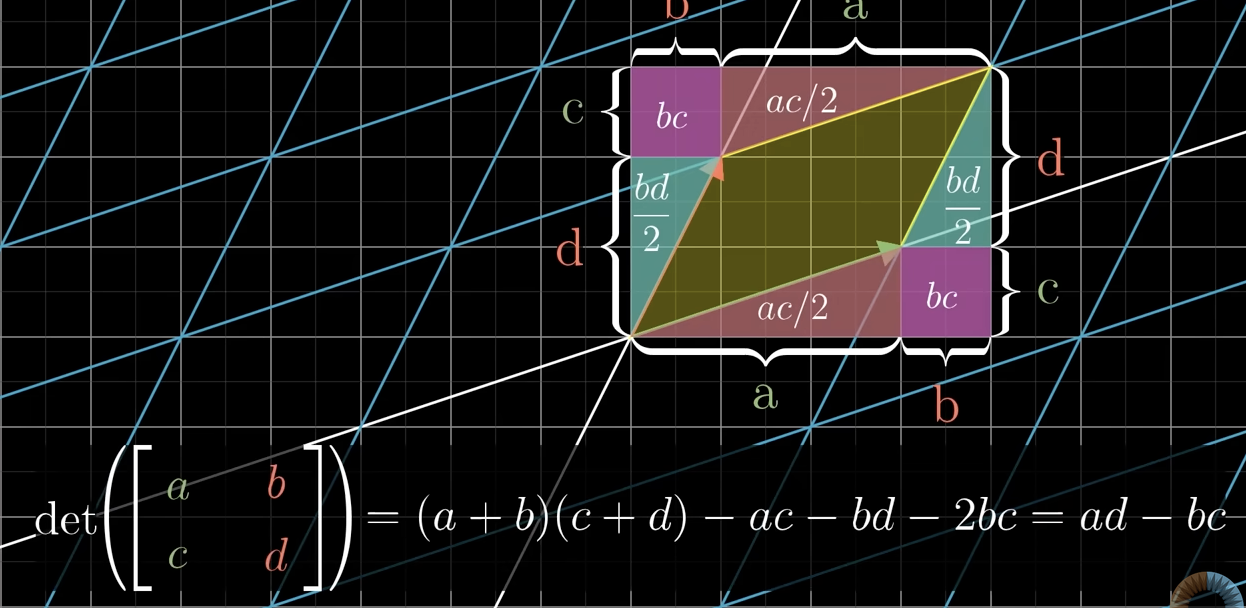
Geometric meaning of determinant in 2D

The determinant equals the area of the parallelogram formed by the matrix’s columns(the scaling of basis vectors).

Geometric meaning in 3D

The determinant equals the volume of the parallelepiped formed by the matrix’s columns.

When the determinant < 0, what happens to the basis vectors.

j was on the left side of i, but after being orientated, j will now be on the right side of i.

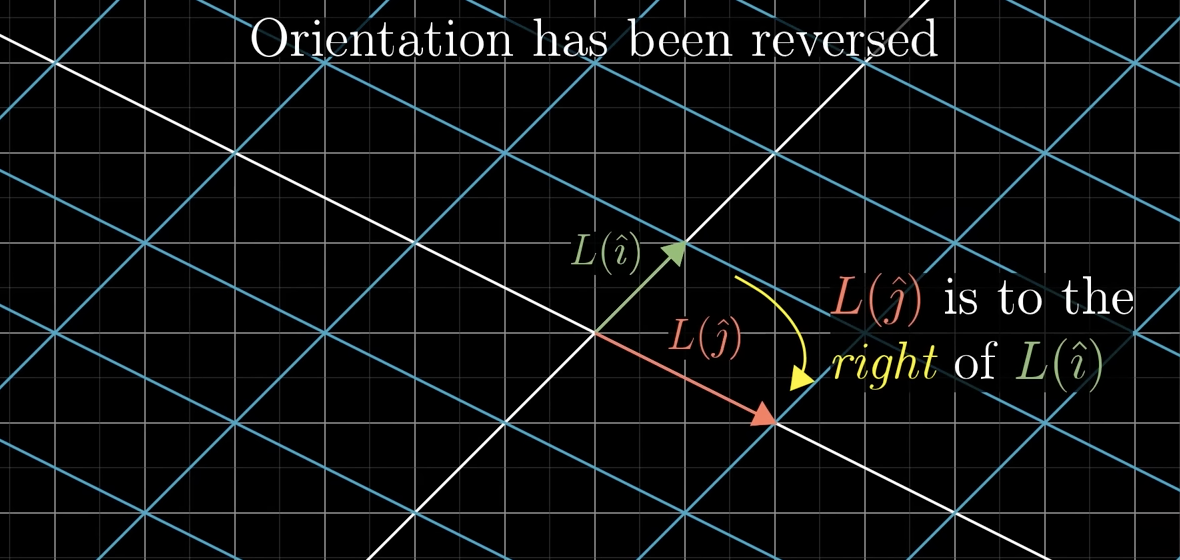
If the determinant is -5, what is the meaning of the absolute value?

It still tells you the factor by which areas have been scaled, so the area will still scale by 5, itll just flip the parallelogram.

If we get the determinant of 0 by a 3×3 matrix, what does that mean geometrically?

This means the volume is 0, it gets squished to either a flat plane, a line, or even a single point (rare).

• This also means the columns (and rows) in the matrix are linearly dependent

What helps to see when the determinant < 0?

Using the right hand rule to see where the k points.

What is the determinant formula?

det(A) = ad-bc

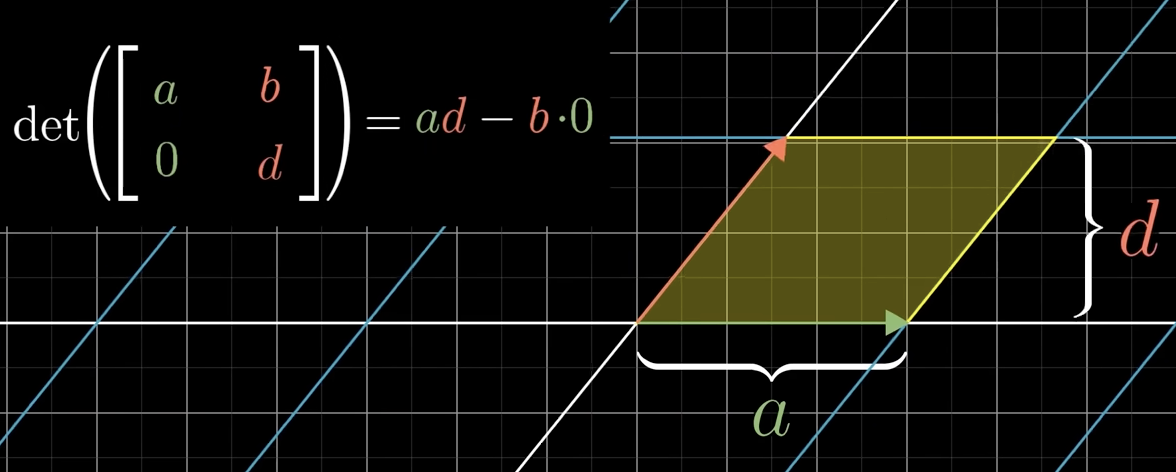
What do the terms ad and bc mean in the determinant formula?

The matrixs columns form a parallelogram.

ad = the forward area contribution

bc = the backward / counter area contribution, tells us how the parallelogram is squished or stretched in the diagonal direction

subtracting gives the signed area of the parallelogram - the determinant.

What is the computation of the determinant for a 3×3 matrix?

Look at picture

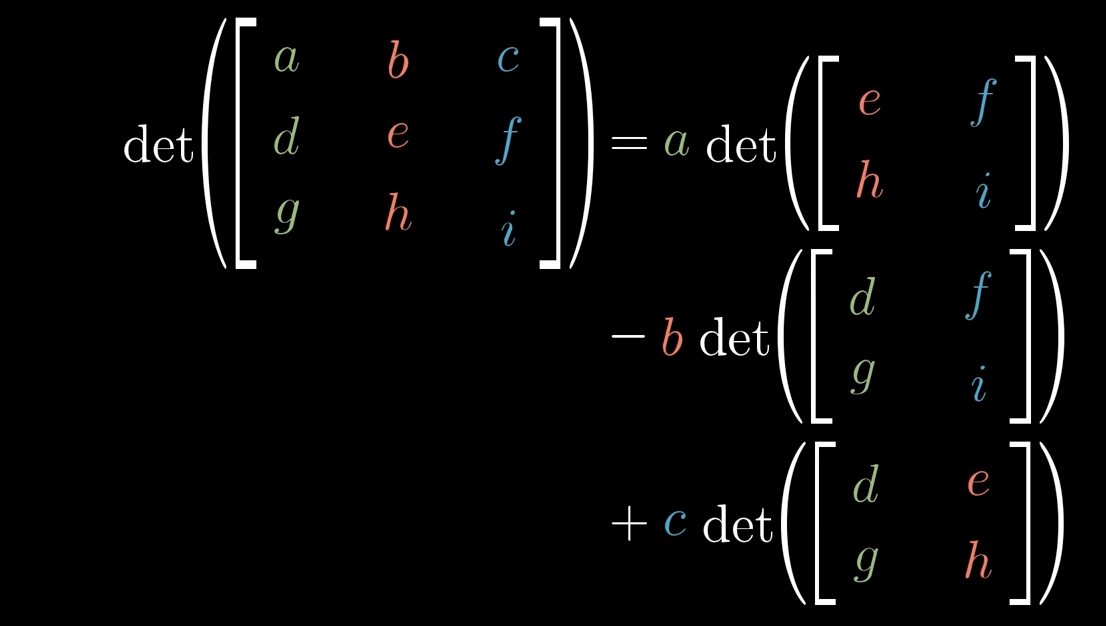
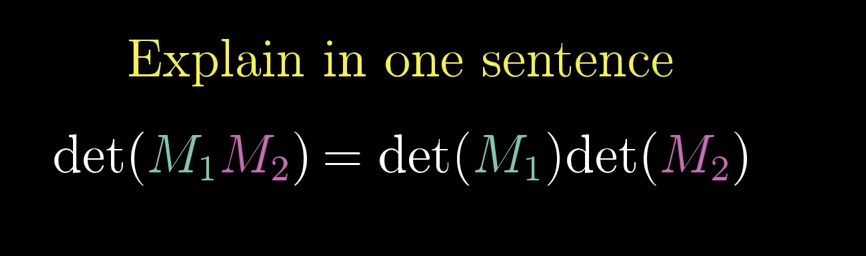
Explain the formula.

The total volume-scaling of two transformations applied in sequence is the product of their individual volume-scalings.