Vectors

How is the 0 vector written?

0 = PP^→

How do you define the set of vectors in n dimensions?

Eⁿ = {PQ^→ : P, Q ∈ ℝⁿ} for all n ∈ N \ {1}.

What does it mean if points are colinear?

if and only if PQ^→ and PR^→ are parallel, which is if and only if

∃ α ∈ R \ {0} such that PQ^→ = αPR^→

What is the formal definition of the vector equation of a line?

{R ∈ ℝ³ : r = p + αq for α ∈ ℝ}

What is the scalar product between 2 vectors?

u · v = |u||v| cos (θ_uv) where θ_uv is the non-reflex angle between u and v. If u and v are perpendicular their dot product is 0

What is the formula for the projection of w onto u?

Given two vectors u and w, the projection of w onto u is the

vector parallel to u given by

proj_u(w) = (w · u/|u|) u/|u|

What is a general right handed system?

Let u, v and w be three non co-planar vectors. Let θ_uv be the non-reflex angle from u to v.

Then u, v and w form a right handed triad or a right handed system.

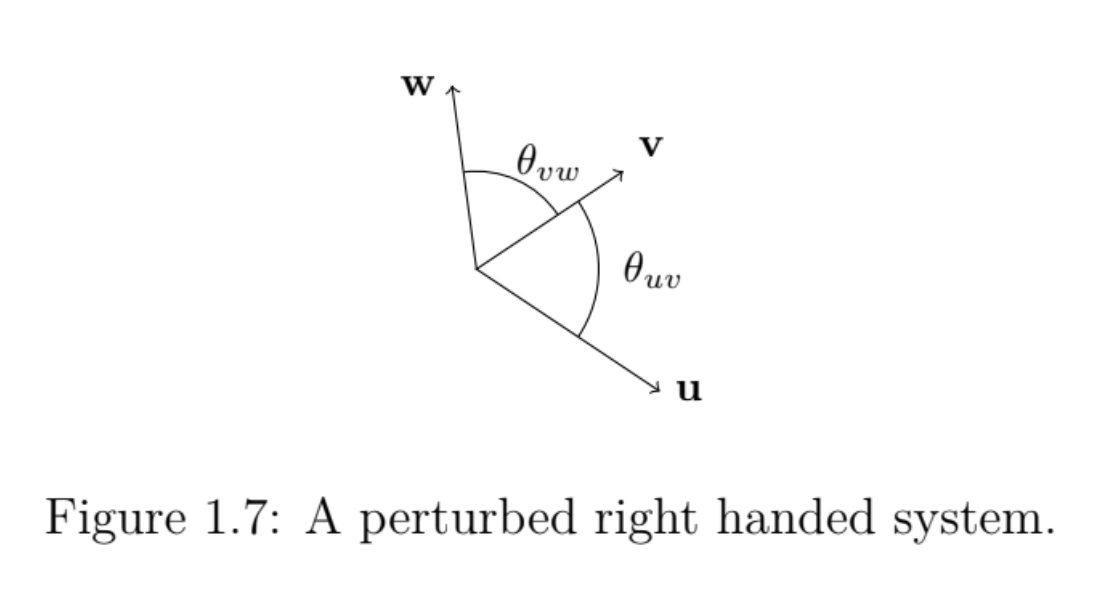
What is the vector product?

If u, v ̸= 0 and u is not parallel to v. Then u × v is a vector with:

(a) magnitude given by,

|u × v| = |u||v|sin θ.

(b) direction perpendicular to both u and v such that u, v and u × v are a right handed triad.

If u and v are non-zero parallel vectors, then u × v = 0.

(3) If u = 0 or v = 0, then u × v = 0

What are the properties of the vector product?

• An internal operation

• Distributive

• Anti-symmetric as u x v = -v x u (not commutative)

• Not associative

• No identity and therefore no inverse

What are the properties of the scalar product?

• Not an internal operation

• Not associative

• No identity and therefore no inverse

• Commutative

What is the normal vector to a plane?

A vector which is perpendicular to the plane. If n is a normal vector, then αn will be a normal vector for α ∈ ℝ \ {0}.

What is the scalar equation of a plane?

n · r = n · p where n is the normal vector to the plane and r and p are vectors on the plane. Thus the scalar equation of a plane perpendicular to vector n is given by n · r = d for some constant d.

What observations can be made from the scalar equation of a plane?

(i) Since n ̸= 0, not all of a, b and c can be zero.

(ii) If d = 0, then the plane intersects the origin.

(iii) In 2-dimensional geometry, the equations x = d, y = d and ax+by = d all represent lines. However, in three dimensions, ax + by = d represents a plane as well as x = d and y = d.

(iv) If U, V and W are three non co-linear points in 3-dimensional space, there is exactly one plane containing all three of them.

What is the vector equation of a plane?

r = p + λ₁v₁ + λ₂v₂ for some λ₁, λ₂ ∈ ℝ where p is a vector on the plane

What are the 3 possible types of intersections between 3 distinct planes?

1. The planes do not intersect.

2. The planes intersect at one point. (sheaf)

3. The planes intersect on a straight line.

What is the equation for a 3D line in standard form?

If r = (x, y, z), p = (p1, p2, p3) and v = (v1, v2, v3), then it is written as (x − p1)/v1 = (y − p2)/v2 = (z − p3)/v3

What is the formula for the perpendicular distance between a point and a plane?

|p · n − d|/|n| where point P has position vector p, n is the normal vector of the plane and n · r = d 

What is the formula for the perpendicular distance between 2 parallel planes?

|d − d’|/|n| where n · r = d 

What are the 3 possible types of intersections between 2 distinct lines?

1. They are parallel and do not intersect

2. They intersect

3. They are not parallel and do not intersect (skew)

What is the formula for the acute angle between 2 lines?

cos θ = | |v · v′| / |v||v′| | where v and v’ are the direction vectors of 2 distinct lines

What is the scalar triple product of three vectors u, v and w?

u · (v x w)

How can the scalar triple product be connected to parallelepipeds?

• It can be interpreted as the signed volume of a parallelepiped (a cuboid with every face parallelogram) i.e. |u||v||w||sin (θ_v,w)| cos (θ_u,v×w) = u · (v × w).

• Also note that the order of vectors defining the parallelepiped matters, due to the right hand rule used to define the vector product (If we switch the labels for the vectors v and w , it follows that v x w is oriented in the opposite direction, which changes the sign of the scalar triple product)

What are some equations involving projections and the vector product?

Let v be a non-zero vector and Π be the plane perpendicular to v that intersects 0. Moreover, let u* be the projection of u onto Π.

u × v = u* × v

(u₁ + u₂)* = u₁* + u₂*

(u₁ + u₂) × v = (u₁ × v) + (u₂ × v)

What is the standard form equation for a line in 3D?

(x − p₁)/v₁ = (y − p₂)_/v₂ = (z − p₃)/v₃

where r = (x, y, z), p = (p₁, p₂, p₃) and v = (v₁, v₂, v₃) from the vector equation of a line r = p + αv

What is the parametric equation for a line in 3D?

x = p₁ + αv₁, y = p₂ + αv₂ and z = p₃ + αv₃,