Quadratics Review FULL

Quadratics review, mostly section 2

Vertex form

f(x)=a(x-h)²+k

Vertex

(h,k)

Negative “a”

Reflects over the x-axis

Positive “a”

Doesn’t reflect over the x-axis

Negative “a” opens

Down

Positive “a” opens

Up

lal>1 stretches

vertically

0<lal<1 stretches

horizontally

lal>1 is

Thinner

0<lal<1 is

Wider

Quadratic function

f(x)=ax²+bx+c

Parent quadratic function

f(x)=x²

The graph of a quadratic function is a

Parabola

a>0 the parabola opens

Upward

a<0 the parabola opens

Downward

h determines which translation

Horizontal

k determines which translation

Vertical

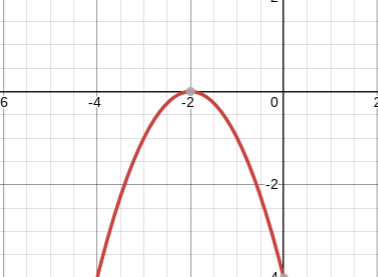
Describe the transformation of the parent function, then graph. Parent function: f(x)=x²

g(x)=-(x+2)²+0

Left 2 units

No vertical shift

Reflects across the x-axis

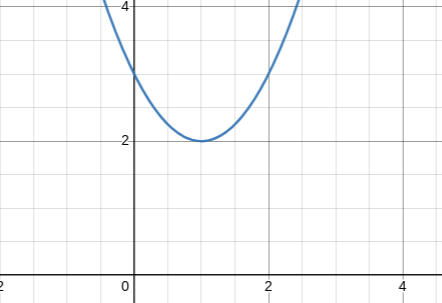
Describe the transformation of the parent function, then graph. Parent function: f(x)=x²

g(x)=(x-1)²+2

Right 1 unit

Up 2 units

No reflection

Axis of symmetry

x=h

Minimum

Lowest point of the Parabola, written as y=k

Maximum

Highest point of the Parabola, written as y=k

Domain

X values of the Parabola written in interval notation

Range

Y values of the Parabola written in interval notation

Identify the key features of f(x)=-(x+4)²-5

Vertex: (-4,-5)

A.O.S: x=-4

Max: y=-5

Domain: R, (-∞, +∞)

Range: {yly≤5}, (-∞,-5]

Key features of a Quadratic function

Vertex

A.O.S

Min/Max

Domain/Range