Big Ω and Θ Notations

Big-O Formal Definition

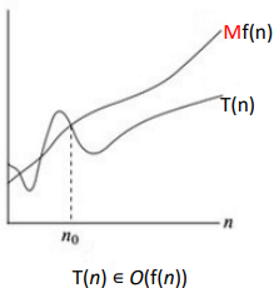
T(n) ∊ O(f(n)) if there are positive constants M and n₀ such that 

• T(n) ≤ M×f(n) for all n ≥ n₀

Big Ω Formal Definition

Let T(n) and f(n) be two positive functions from the integers or the real numbers to the real numbers 

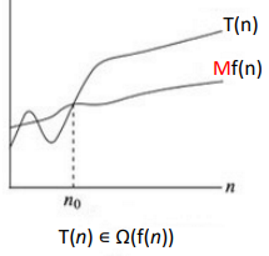
T(n) is Ω(f(n)) if even as n becomes arbitrarily large, T(n)'s growth is bounded from below by f(n), meaning it grows no slower than f(n) 

T(n) ∊ Ω(f(n)) if there are positive constants M and n₀ such that 

• T(n) ≥ M×f(n) for all n ≥ n₀

Big Θ Formal Definition

Let T(n) and f(n) be two positive functions from the integers or the real numbers to the real numbers 

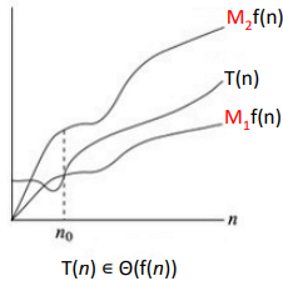
T(n) is Θ(f(n)) if even as n becomes arbitrarily large, T(n)'s growth is bounded from above and below by f(n), meaning it grows no faster and no slower than f(n) 

T(n) ∊ Θ(f(n)) if there are positive constants M1, M2 and n₀ such that 

• M1×f(n) ≤ T(n) ≤ M2 ×f(n) for all n ≥ n₀

It means T(n) ∊ Θ(f(n)) if T(n) ∊ O(f(n)) AND T(n) ∊ Ω(f(n))

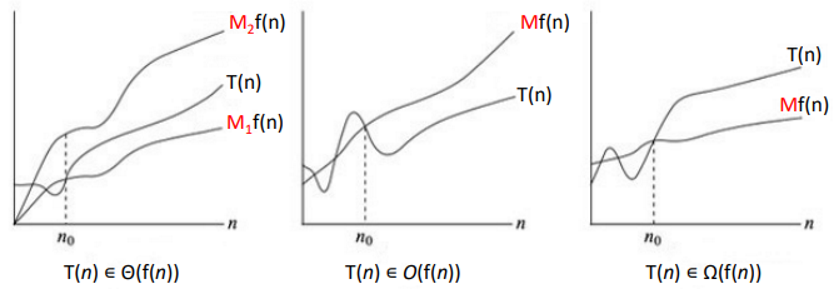
Big O, Big Ω, Big Θ Graphs

In General

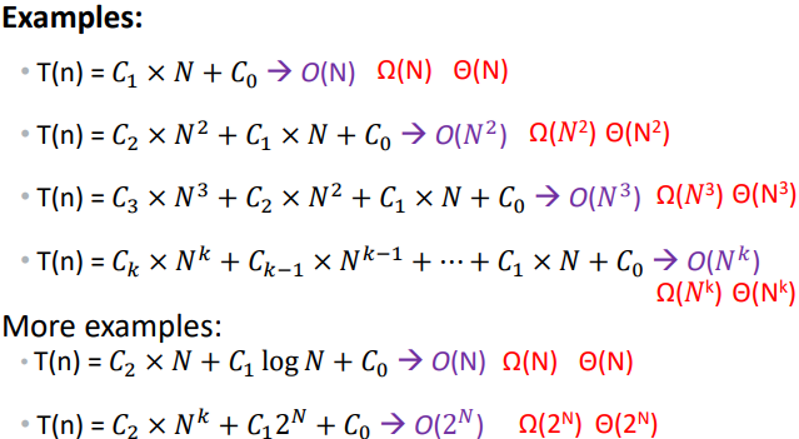
Is Linear Search O(n)?

yes, there is no input of size n for which the runtime is not bounded from above by n 

• Best case O(1), O(log n), O(n), …. 

• Average case O(n), O(nlog n), O(n^2), ….. 

• Worst case O(n), O(nlog n), O(n^2), …..

Is Linear Search Ω(1)?

yes ,there is no input of size n that takes less than a constant amount of time 

true for every algorithm 

• Best case Ω(1) 

• Average case Ω(n), Ω(log n), Ω(1) 

• Worst case Ω(n), Ω(log n), Ω(1)

Is Linear Search Θ(n)?

no, there is an input of size n, the best case, specifically, for which the runtime is Θ(1) 

• Best case Θ(1) 

• Average case Θ(n) 

• Worst case Θ(n)

Big O

rate of growth of an algorithm is <= a specific value

defined as upper bound

Big Ω

rate of growth is >= a specific value

defined as a lower bound and lower

Big Θ

rate of growth is == to a specific value

defined as tightest bound, best of all the worst case times that the algorithm can take