exponentials and logarithms (y1)

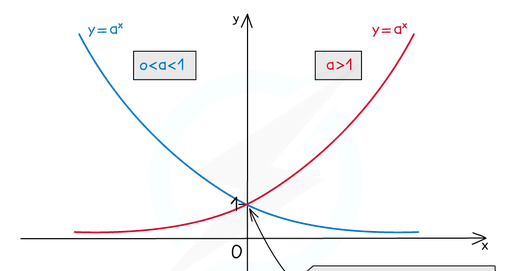
exponential functions

f(x) = a^x

e

an irrational mathematical constant, 2.71828...

the point at which an exponential function's graph and the graph of its gradient function is the same

if y = e^x, dy/dx = e^x

exponential growth/decay

where the rate of increase/decrease is proportional to the size- i.e. grows by x% each year

exponential modelling

e^x is suitable to model exponential growth, and e^-x is suitable to model exponential decay

logarithms

the inverse of exponential functions

loga n = x is equivalent to a^x = n

i.e. log3 9 = 2 is equivalent to 3^2 = 9

laws of logarithms- +/-

loga x + loga y = loga xy

loga x - loga y = loga x/y

laws of logarithms- x^k

loga (x^k) = kloga x

laws of logarithms special cases

loga 1/x = loga (x^-1) = -loga x

loga a = 1

loga 1 = 0

logarithms and non linear data

if y = ax^n then the graph of log y against log x will be a straight line with gradient n and vertical intercept log a

natural log

ln- equivalent to log e

e^(ln x) = x

logarithmic graphs

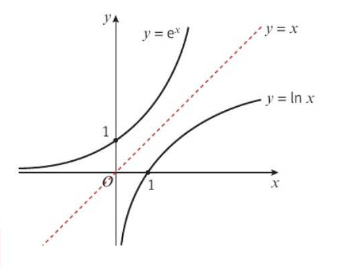
the graph of y = ln x and the graph of y = e^x are reflections in the line y=x

as y = ln x does not cross the y axis it is only defined where x is positive