6.1 Inner Product, Length, and Orthogonality

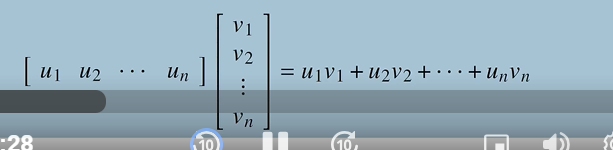
the inner product or dot product of two vectors u and v is u • v is 

u^Tv

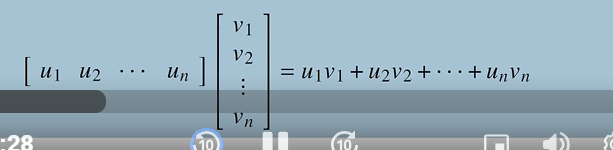
properties of the inner product

u • v = v • u

(u+v) • w = u • w + v • w

cu • v= c(u•v) = u•cv

u•u >= 0 and u • u = 0 if and only if u =0

the length or norm of v is the nonnegative scalar ||v|| defined by

||v|| = sqrt(v•v) = sqrt(v₁² + v₂² +….v_n² )

||v||² =

v • v

a vector that has length 1 is called a

unit vector

normalizing the vector: if we divide a vector by its ? we obtain a unit vector that is in the same ? as the original

length, direction

length =

1

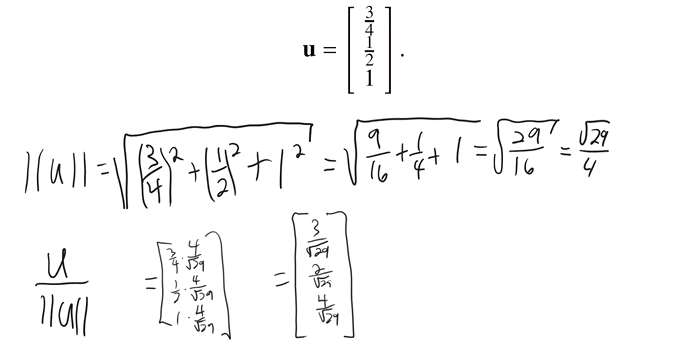
example of finding the unit vector in tge direction of a given vector

the distance between two vectors is

dist(u,v) =

||u-v||

= sqrt(u₁ - v₁)² + …. (u_n - v_n)²)

vectors u and v are orthoganl to each other if u • v = ?

0

u and v are orthoganal to each other if and only if ||u+v||² = ?

||u||² + ||v||²

the orthogonal complement of a subspace W is denoted as W⟂ and it is defined as ?

the set of all vectors orthogonal to every vector in W

a vector x is in W⟂ if and only if

x is orthogonal to every vector in the set that spans W and W⟂ is a subspace of Rⁿ

row(A)⟂ = ?

nul(A)

col(A)⟂ =

nul(A^T)

this is because the columns of A are the rows of A^T

the angle between u and v is defined to be theta and satisfies that u • v = ?

||u||||v||cos(theta)

to find the angle between the two vectors u and v you need to calculate

theta = arccos(u•v/||u||||v||)

angle will always be between 0 and 180 degrees

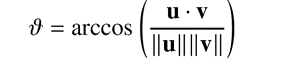
(T/F) ⋅v⋅v=∥v∥².

True

(T/F) u⋅v−v⋅u=0.

True

(T/F) If the distance from u to v equals the distance from u to −v, then u and v are orthogonal.

true

(T/F) If ∥u∥2+∥v∥2=∥u+v∥2, then u and v are orthogonal.

True

(T/F) If vectors v1, …, vp, span a subspace W and if x is orthogonal to each vj for j=1,…,p, then x is in W⊥

true

(T/F) If x is orthogonal to every vector in a subspace W then x is in W⊥.

True

(T/F) For any scalar c, ∥cv∥=c∥v∥.

False; the absolute sign is missing

(T/F) For any scalar c, u⋅(cv)=c(u⋅v).

true

(T/F) For a square matrix A, vectors in Col A are orthogonal to vectors in Nul A.

FALSE; counterexample: [ 1 1; 0 0]

(T/F) For an m×n matrix A, vectors in the null space of A are orthogonal to vectors in the row space of A.

true

Let u=(u1, u2, u3). Explain why ⋅u⋅u≥0. When is ⋅u⋅u=0?

Since u ⋅ u is the sum of the squares of the entries in u, u ⋅ u ≥ 0. The sum of squares of numbers is zero if and only if all the numbers are themselves zero.

||u+v||² =

(u+v ) . (u+v )

||u||²

u . u

Show that if x is in both W and W⊥, then x=0.

Suppose that x is in W and W⊥ Since x is in W⊥, x is orthogonal to every vector in W, including x itself. So x ⋅ x = 0, which happens only when x = 0.