Two paired continuous variables

TWO PAIRED CONTINUOUS VARIABLES

What does a paired samples t-test evaluate? (t.test() or pairedSamplesTTest())

Formal name: Student’s paired samples t-test

It compares the means of two related groups (e.g., before vs. after measurements on the same subjects).

• H₀: the mean difference between the paired groups is zero

  • the difference between the population means for both samples is zero

• H₁: the mean difference is not zero

  • the difference between the population means for both samples is not zero

What is the test statistic for a paired samples t-test and how are degrees of freedom calculated?

• dˉ = mean of the differences

• sd​ = standard deviation of the differences

• n = number of paired observations

*Values further away from zero (i.e., higher absolute values) correspond to a lower probability of H0 being true

Degrees of freedom: df = N−1

• N is the number of observations in the data set

*exact rejection regions depend on degrees of freedom

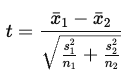
What is Cohen’s d and how is it interpreted for paired samples t-tests? - Effect size

Cohen’s d measures the size of the mean difference:

• 0.20 = small effect

• 0.50 = medium effect

• 0.80 = large effect

*larger values correspond to a greater difference difference in means

What assumptions does the paired samples t-test have?

• The differences between paired observations are normally distributed

  • Check with: Shapiro-Wilk test, histogram, Q-Q plot

  • If normality is violated: use the Wilcoxon signed-rank test (wilcox.test())

(???? chat said:)

• Observations within pairs are related; observations across pairs are independent