MCHE 3310 Quiz 1
0.0(0)
Card Sorting
1/77
There's no tags or description
Looks like no tags are added yet.
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
78 Terms
1
New cards
Atomic Mass Unit (amu)
1/12 the mass of a carbon-12 atom
2
New cards
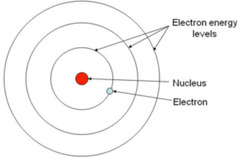
Bohr Model
1) Electrons revolve around the atomic nucleus in discrete orbitals
2) The position of any particular electron is defined by its orbital
3) The electron energies of electrons are quantized - electrons are permitted to have only specific values of energy
2) The position of any particular electron is defined by its orbital
3) The electron energies of electrons are quantized - electrons are permitted to have only specific values of energy
3
New cards
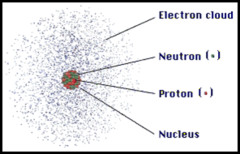
Wave-Particle Model
1) Electron exhibits both wave-like and particle-like characteristics
2) Position of an electron is described by a probability distribution or electron cloud
2) Position of an electron is described by a probability distribution or electron cloud
4
New cards
Quantum Numbers
Set of numbers used to completely describe an electron
5
New cards
Principle Quantum Number
1) Symbolized by "n"
2) Designates shell
n = 1, 2, 3, 4, 5...
Letter = K, L, M, N, O...
2) Designates shell
n = 1, 2, 3, 4, 5...
Letter = K, L, M, N, O...
6
New cards
Second Quantum Number
1) Symbolized by "l"
2) Designates subshell
3) Electron orbital shapes depend upon this
4) Range from 0 to (n - 1)
l = 0, 1, 2, 3...
Subshell = s, p, d, f
2) Designates subshell
3) Electron orbital shapes depend upon this
4) Range from 0 to (n - 1)
l = 0, 1, 2, 3...
Subshell = s, p, d, f
7
New cards
Third (Magnetic) Quantum Number
1) Symbolized by "ml"
2) Determines number of electron orbitals for each subshell
3) It's an integer between -l and +l, including 0
1 s orbital
3 p orbitals
5 d orbitals
7 f orbitals
2) Determines number of electron orbitals for each subshell
3) It's an integer between -l and +l, including 0
1 s orbital
3 p orbitals
5 d orbitals
7 f orbitals
8
New cards
Fourth Quantum Number
1) Symbolized by "ms"
2) It's the spin moment and is oriented either up or down (2 electrons per electron orbital)
3) +1/2 for spin up, -1/2 for spin down
2) It's the spin moment and is oriented either up or down (2 electrons per electron orbital)
3) +1/2 for spin up, -1/2 for spin down
9
New cards
Pauli Exclusion Principle
No two electrons in the same atom can have the same set of four quantum numbers

10
New cards
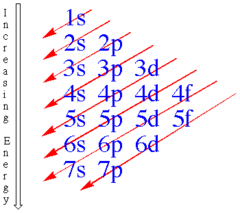
Orbital Filling Sequence
Electrons tend to occupy the lowest available energy states.
11
New cards
Valence Electrons
1) Most available for bonding and tend to control chemical properties
2) Present in the outer-most shell
3) For example, When bonding with iron (Fe), even though the 4s subshell has less energy than the 3d subshell, the iron atom loses the 4s electrons first because they're on the outer-most shell
2) Present in the outer-most shell
3) For example, When bonding with iron (Fe), even though the 4s subshell has less energy than the 3d subshell, the iron atom loses the 4s electrons first because they're on the outer-most shell
12
New cards
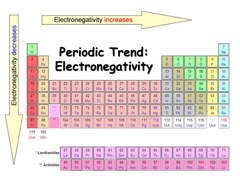
Electronegativity
1) Ranges from 0.9 to 4.1
2) Smaller values tend to give away electrons while larger values tend to acquire electrons
2) Smaller values tend to give away electrons while larger values tend to acquire electrons
13
New cards
Primary Bonding Type: Ionic
1) Occurs between metallic and nonmetallic elements
2) Requires electron transfer
3) Large difference in electronegativity required
4) Make for poor conductors and have low chemical reactivity
5) ex. NaCl
2) Requires electron transfer
3) Large difference in electronegativity required
4) Make for poor conductors and have low chemical reactivity
5) ex. NaCl
14
New cards
Primary Bonding Type: Covalent
1) Similar Electronegativity (sharing electrons)
2) Bonds are determined by valence, where s & p orbitals dominate bonding
3) Directional bonding between nonmetallic elemental molecules
4) Make for poor conductors and have varying mechanical properties
5) ex. H2
2) Bonds are determined by valence, where s & p orbitals dominate bonding
3) Directional bonding between nonmetallic elemental molecules
4) Make for poor conductors and have varying mechanical properties
5) ex. H2
15
New cards
Primary Bonding Type: Metallic
1) Mainly found in metals and their alloys
2) Valence electrons are not bound to any particular atom and are free to drift through the entire metal (electrons act as the glue that holds the ion cores together)
3) Non-directional bonding with bonding energy from 62 kJ/mol to 850 kJ/mol
2) Valence electrons are not bound to any particular atom and are free to drift through the entire metal (electrons act as the glue that holds the ion cores together)
3) Non-directional bonding with bonding energy from 62 kJ/mol to 850 kJ/mol
16
New cards
Primary Bonding Combinations
Most materials possess a combination of different bonds, making generalization of bonding difficult
17
New cards
Secondary Bonding: Van der Waals
1) Arise from atomic or molecular dipoles
2) Two types of dipoles: induced and permanent
3) Bonding energy around 4-30 kJ/mol
4) Induced dipole ex. H2, Cl2, etc.
5) Permanents dipole ex. HCl, HF, etc.
2) Two types of dipoles: induced and permanent
3) Bonding energy around 4-30 kJ/mol
4) Induced dipole ex. H2, Cl2, etc.
5) Permanents dipole ex. HCl, HF, etc.
18
New cards
Secondary Bonding: Hydrogen Bond
1) Attractive interaction between a hydrogen atom with an electronegative atom (intermolecular bond)
2) Stronger than Van der Waals interaction but far weaker than covalent or ionic bonds
3) ex. bond between lone pair of oxygen and hydrogen in H2O
2) Stronger than Van der Waals interaction but far weaker than covalent or ionic bonds
3) ex. bond between lone pair of oxygen and hydrogen in H2O
19
New cards
Energy and Packing
Dense, ordered packed structures tend to have lower energies while non-dense, random structures tend to have higher energies
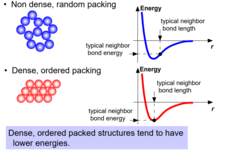
20
New cards
Crystalline Materials
1) atoms pack in periodic, 3D arrays
2) typical of : metals, many ceramics, some polymers
2) typical of : metals, many ceramics, some polymers

21
New cards
Noncrystalline Materials
1) atoms have no periodic packing
2) Occurs for complex structures and rapid cooling
2) Occurs for complex structures and rapid cooling
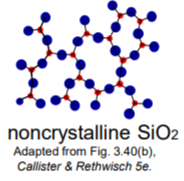
22
New cards
FCC Packing
1) ABCABCABC...
2) The atoms in rows A & C aren't aligned
2) The atoms in rows A & C aren't aligned
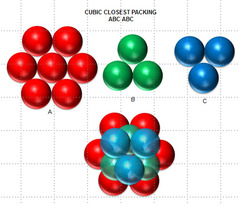
23
New cards
HCP Packing
1) ABABAB...
2) The atoms of the third plane are in exactly the same position as the atoms in the first plane
2) The atoms of the third plane are in exactly the same position as the atoms in the first plane
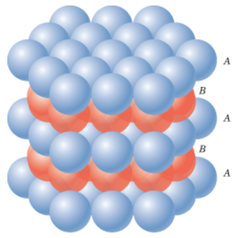
24
New cards
Hard Sphere Model
Atoms (or ions) are thought of as being solid spheres having well-defined diameters where spheres representing nearest-neighbor atom touch one another
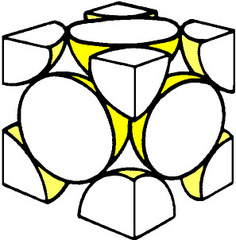
25
New cards
Unit Cell
The smallest component of the crystal that reproduces the whole crystal when stacked together with purely translational repetition
Note: more than one unit cell can be chosen for a given crystal structure, but the one with highest symmetry is chosen
Note: more than one unit cell can be chosen for a given crystal structure, but the one with highest symmetry is chosen
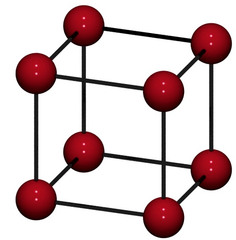
26
New cards
Lattice
1) Infinite, periodic array of mathematical points in which each point has identical surroundings to all others
2) Lattice points are purely mathematical whereas atoms are physical objects
3) Lattice points don't necessarily lie at the center of atoms
2) Lattice points are purely mathematical whereas atoms are physical objects
3) Lattice points don't necessarily lie at the center of atoms
27
New cards
Crystal Structure
Periodic arrangement of atoms in the crystal that can be described by a lattice and a basis
28
New cards
Parameters of a Unit cell
(a, b, c) correspond to the length of the 3 adjacent edges of the unit cell
(α, β, γ) correspond to the 3 angles subtended by the lattice cell axes
(α, β, γ) correspond to the 3 angles subtended by the lattice cell axes
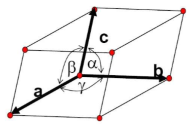
29
New cards
Crystal Systems and Bravais Lattices
1) 7 possible combinations of (a, b, c) and (α, β, γ) resulting in 7 crystal systems
2) The 7 crystal systems can be described using 14 point lattices
2) The 7 crystal systems can be described using 14 point lattices

30
New cards
Cubic
a = b = c
α = β = γ = 90°
α = β = γ = 90°
31
New cards
Tetragonal
a = b ≠ c
α = β = γ = 90°
α = β = γ = 90°
32
New cards
Orthorhombic
a ≠ b ≠ c
α = β = γ = 90°
α = β = γ = 90°
33
New cards
Hexagonal
a = b ≠ c
α = β = 90°
γ = 120°
α = β = 90°
γ = 120°
34
New cards
Trigonal
a = b = c
α = β = γ ≠ 90°
α = β = γ ≠ 90°
35
New cards
Monoclinic
a ≠ b ≠ c
α = γ = 90°
β ≠ 90°
α = γ = 90°
β ≠ 90°
36
New cards
Triclinic
a ≠ b ≠ c
α ≠ β ≠ γ ≠ 90°
α ≠ β ≠ γ ≠ 90°
37
New cards
Simple Cubic (SC)
Atoms are situated only at the corners of the unit cell (1 atoms per unit cell)
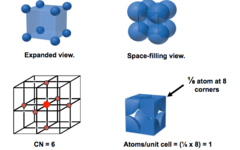
38
New cards
Body Centered Cubic (BCC)
Atoms are situated at the corners in addition to a single atom at the center of the unit cell (2 atoms per unit cell)
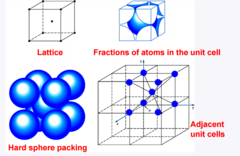
39
New cards
Face Centered Cubic (FCC)
Atoms are situated at the corners and on the face of each unit cell (4 atoms per unit cell)
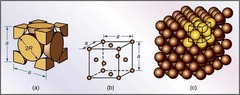
40
New cards
Coordination Number
The number of ions of opposite charge surrounding each ion in a crystal
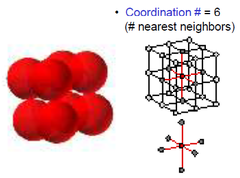
41
New cards
Atomic Packing Factor (SC)
APF = Volume of atoms in unit cell / Volume of unit cell
APF (SC) = 0.52
APF (SC) = 0.52
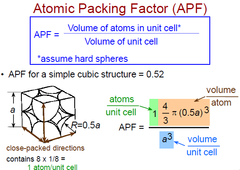
42
New cards
Atomic Packing Factor (BCC)
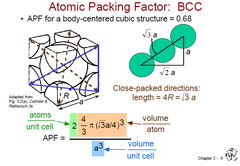
APF = Volume of atoms in unit cell / Volume of unit cell
APF (BCC) = 0.68
APF (BCC) = 0.68
43
New cards
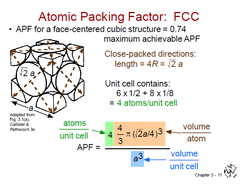
Atomic Packing Factor (FCC)
APF = Volume of atoms in unit cell / Volume of unit cell
APF (FCC) = 0.74
APF (FCC) = 0.74
44
New cards
Theoretical Density
Mass of Atoms in Unit Cell / Total Volume of Unit Cell
ρ = n*A / Vc*Na
n = number of atoms / unit cell
A = atomic weight
Vc = volume of unit cell
Na = Avogadro's number
ρ = n*A / Vc*Na
n = number of atoms / unit cell
A = atomic weight
Vc = volume of unit cell
Na = Avogadro's number
45
New cards
Point Coordinates of Unit Cell
1) Any point within a unit cell is specified as fractional multiples of the unit cell edge lengths
2) Position "P" specified as "q r s"; convention: coordinates aren't separated by commas or punctuation
2) Position "P" specified as "q r s"; convention: coordinates aren't separated by commas or punctuation
46
New cards
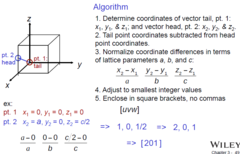
Crystallographic Directions
Directional indices highlighting difference between vector head and tail
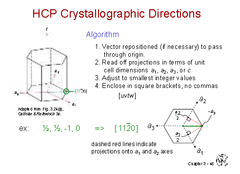
Algorithm:
1) Determine coordinates of vector tail and vector head
2) Tail point coordinates subtracted from head point coordinates
3) Normalize coordinate differences in terms of lattice parameters "a", "b", and "c"
4) Adjust to smallest integer values
5) Enclose in square brackets with no commas
Nuances:
1) Parallel lines have the same indices
2) No matter the length, one line has just one indices
Algorithm:
1) Determine coordinates of vector tail and vector head
2) Tail point coordinates subtracted from head point coordinates
3) Normalize coordinate differences in terms of lattice parameters "a", "b", and "c"
4) Adjust to smallest integer values
5) Enclose in square brackets with no commas
Nuances:
1) Parallel lines have the same indices
2) No matter the length, one line has just one indices
47
New cards
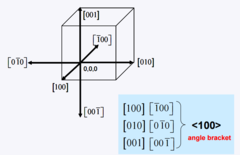
Family of Directions
Angular bracket < > indicates a family of directions called a form (set of equivalent directions)
48
New cards
HCP Crystallographic Directions
Defined using Miller indices with a non-rectilinear coordinate system
49
New cards
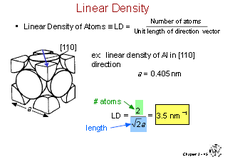
Linear Density (LD)
Number of atoms / unit length of direction vector
50
New cards
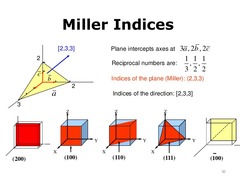
Crystallographic Planes
Specified by 3 Miller indices (hkl)
Procedure:
1) If plane passes through origin, translate plane or choose new origin
2) Determine intercepts of planes on each of the axes in terms of unit cell edge lengths, known as lattice parameters (a plane that parallels an axis can be considered to have an infinite intercept)
3) Determine the reciprocal of the three intercepts (reciprocal of infinity is 0)
4) If necessary, multiply or divide to convert to smallest integers
5) The three indices are not separated by commas and are enclosed in parentheses (hkl)
6) If indices are negative, a bar is placed on top of index
Procedure:
1) If plane passes through origin, translate plane or choose new origin
2) Determine intercepts of planes on each of the axes in terms of unit cell edge lengths, known as lattice parameters (a plane that parallels an axis can be considered to have an infinite intercept)
3) Determine the reciprocal of the three intercepts (reciprocal of infinity is 0)
4) If necessary, multiply or divide to convert to smallest integers
5) The three indices are not separated by commas and are enclosed in parentheses (hkl)
6) If indices are negative, a bar is placed on top of index
51
New cards
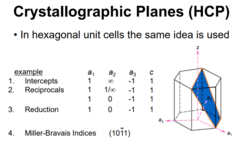
Crystallographic Planes (HCP)
In hexagonal unit cells a similar Miller-Bravais approach is used
52
New cards
Family of Crystalline Planes
1) { } indicates family of planes
2) All planes in the same family are crystallographically equivalent
2) All planes in the same family are crystallographically equivalent
53
New cards
Planar Density (PD)
Number of atoms per 2D repeating unit / Area per 2D repeating unit
54
New cards
Single vs Polycrystals
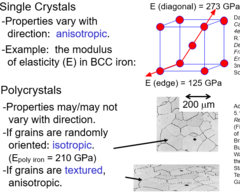
55
New cards
X-Ray Diffraction
1) The scattering of X-rays by the regularly spaced atoms of a crystal, useful in obtaining information about the structure of the crystal
2) The magnitude of the distance between two adjacent, parallel planes of atoms is a function of the Miller indices as well as the lattice parameters
2) The magnitude of the distance between two adjacent, parallel planes of atoms is a function of the Miller indices as well as the lattice parameters
56
New cards
Crystalline Defect
A lattice irregularity having one or more of its dimensions on the order of an atomic diameter
57
New cards
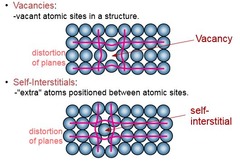
Point Defects
2 types:
1) Vacancies: vacant atomic sites in a structure
2) Self-Interstitials: "extra" atoms positioned between atomic sites (less likely in metals as it's difficult to get a large metal atom into the small vacancy)
1) Vacancies: vacant atomic sites in a structure
2) Self-Interstitials: "extra" atoms positioned between atomic sites (less likely in metals as it's difficult to get a large metal atom into the small vacancy)
58
New cards
Equilibrium Concentration of Vacancies
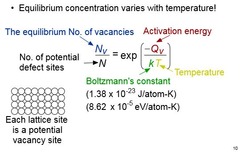
59
New cards
Alloy
1) A metal comprised of two or more elements, at least one of which is metallic
2) More abundant element is referred to as the solvent and the less abundant element is the solute
3) Generally, metals do not like to mix, but when they do they form in one of two ways: substitution (element replaces host atom in orderly arrangement) and interstitial (smaller element goes into interstitial voids in an orderly arrangement)
4) The substitutional and interstitial atoms can be thought of as point defects
2) More abundant element is referred to as the solvent and the less abundant element is the solute
3) Generally, metals do not like to mix, but when they do they form in one of two ways: substitution (element replaces host atom in orderly arrangement) and interstitial (smaller element goes into interstitial voids in an orderly arrangement)
4) The substitutional and interstitial atoms can be thought of as point defects
60
New cards
Hume-Rothery Rules for Alloys
For an alloy to be called substitutional solid, it needs to be:
1) Solute and solvent are soluble
2) Be able to form a homogeneous solution
3) Host structure maintains
4) No new structures (phases) are formed
Empirical Rules:
1) Atomic size factor (size difference between the elements should not be greater than 15%)
2) Crystal structure (the crystal structure for metals must be the same)
3) Electronegativity (must have similar electronegativity values)
4) Valences (a metal will have a greater tendency to dissolve a metal of higher valency than of lower valency; higher in lower alright, lower in higher is a fight)
1) Solute and solvent are soluble
2) Be able to form a homogeneous solution
3) Host structure maintains
4) No new structures (phases) are formed
Empirical Rules:
1) Atomic size factor (size difference between the elements should not be greater than 15%)
2) Crystal structure (the crystal structure for metals must be the same)
3) Electronegativity (must have similar electronegativity values)
4) Valences (a metal will have a greater tendency to dissolve a metal of higher valency than of lower valency; higher in lower alright, lower in higher is a fight)
61
New cards
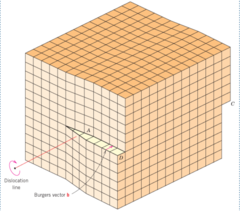
Edge Dislocation
1) extra half plane of atoms inserted in a crystal structure
2) Burgers vector perpendicular to dislocation line
2) Burgers vector perpendicular to dislocation line
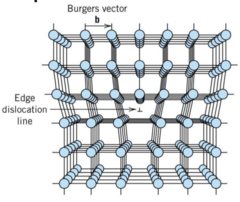
62
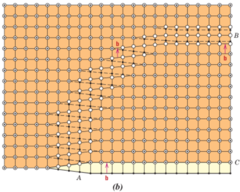
New cards
Screw Dislocations
Result of shear forces on part of the material that caused the displacement of a portion of the crystal
63
New cards
Mixed Dislocations
1) Combination of edge and screw dislocations
2) Relationship between burgers vector and dislocation line is neither perpendicular or a parallel
2) Relationship between burgers vector and dislocation line is neither perpendicular or a parallel
64
New cards
Planar Defects
Boundaries that have two dimensions and normally separate regions of the materials that have different crystal structure and/or crystallographic orientation
65
New cards
External Surfaces
Surface atoms are not bonded to the maximum number of nearest neighbors, making them have higher energy and high reactivity
66
New cards
Grain Boundaries
1) Regions between grains
2) Transition from lattice of one region to that of the other
3) Small-angle grain boundaries have larger energy than high-angle grain boundaries, but neither have higher energy than external surfaces
2) Transition from lattice of one region to that of the other
3) Small-angle grain boundaries have larger energy than high-angle grain boundaries, but neither have higher energy than external surfaces
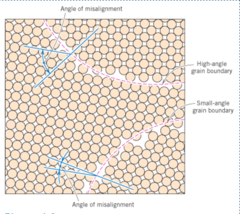
67
New cards
Twin Boundary (plane) and Stacking Faults
A reflection of atom positions across the twin plane and an error in the packing sequence
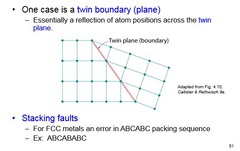
68
New cards
Diffusion
Mass transport by atomic motion
Diffusion is important for the treatment of materials to improve material
properties and materials performance in service
The impurity atoms can be provided from an adjacent another solid
phase, a liquid, or a gas.
Diffusion is important for the treatment of materials to improve material
properties and materials performance in service
The impurity atoms can be provided from an adjacent another solid
phase, a liquid, or a gas.
69
New cards
Inter-diffusion
Atoms of one metal diffuse into another.
70
New cards
concentration gradient
Driving force for diffusion
from regions of high
concentration to regions of low concentration
from regions of high
concentration to regions of low concentration
71
New cards
self-diffusion
In pure metals, atoms also migrate; but all
atoms exchanging positions are of the same type.
atoms exchanging positions are of the same type.
72
New cards
For an atom to diffuse, two conditions must be met:
•There must have
an empty adjacent site
• The atom must have
sufficient energy to break bonds
with its neighbor atoms and then
cause some lattice distortion during the displacement.
an empty adjacent site
• The atom must have
sufficient energy to break bonds
with its neighbor atoms and then
cause some lattice distortion during the displacement.
73
New cards
vacancy diffusion
atoms exchange with vacancies
• applies to substitutional impurities atoms
• rate depends on:
--number of vacancies
--activation energy to exchange
• applies to substitutional impurities atoms
• rate depends on:
--number of vacancies
--activation energy to exchange
74
New cards
interstitial diffusion
•Smaller atoms, e.g., H, C, N and O, can diffuse into or between interstitial positions.
•Interstitial diffusion occurs much more rapidly than vacancy diffusion
•There are more empty interstitial position than vacancies in a solid.
•Interstitial diffusion is an important method to improve materials' mechanical
properties, particularly the surface hardness and strength.
•Interstitial diffusion occurs much more rapidly than vacancy diffusion
•There are more empty interstitial position than vacancies in a solid.
•Interstitial diffusion is an important method to improve materials' mechanical
properties, particularly the surface hardness and strength.
75
New cards
case hardening
Diffuse carbon atoms
into the host iron atoms
at the surface.
into the host iron atoms
at the surface.
76
New cards
Processing using diffusion
Doping silicon with phosphorus for n-type or p-type semiconductors.
1. Deposit P rich layers on surface.
2. Heat it.
3. Result: Doped
semiconductor
regions
1. Deposit P rich layers on surface.
2. Heat it.
3. Result: Doped
semiconductor
regions
77
New cards
steady-state diffusion
Rate of diffusion is independent of time
•
Flux proportional to
concentration gradient
•
Flux proportional to
concentration gradient
78
New cards
Activation energy
the energy required to produce the diffusive motion of one mole of atoms