Descriptive Statistics

Population

Is a complete set of persons or objects that possess some common characteristics that is of interest to the researcher.

Target, Accessible Population

The population for a study usually is described as being composed of two groups?

Target Population

• Which is also called the universe is composed of the entire group of people or objects to which the researcher wishes to generalize the findings of the study.

• Consists of people or things that meet the designated set of criteria of interest to the researcher.

Accessible Population

• It is aggregate of cases that confirm to designated criteria and are also accessible as subjects for study.

• By identifying the group from which the study sample was chosen, the investigator about the conclusion of the generalize ability of research findings.

Sample

May be defined as representative unit of target population which is to be worked upon by researchers during their study.

Quantitative researchers

• Often select samples that will allow them to achieve stating conclusion validity and generalize their result. They therefore develop a sampling plan that specifies in advance how study participants are to selected and how many to include.

Qualitative researchers

• Make sampling decision during the course of data collection based on information & theoretical need & typically do not develop a formal sampling plan in advance.

Principles of Sampling

1. Principle or Law of statistical regularity

   • Large sample size

   • Random Selection

2. Principle of inertia of large numbers

3. Principle of validity

4. Principle of optimization

Principle or Law of statistical regularity

Principles of Sampling

• This law is based upon mathematical theory of probability. It is based upon the following two conditions.

  • Large sample size and random collection

Large sample size

Principles of Sampling: Principle or Law of statistical regularity

• As the sample size increases, the true characteristics of the population are more likely to reveal.

Random Selection

Principles of Sampling: Principle or Law of statistical regularity

• The sample should be selected randomly in which each and every unit of the universe has an equal chance of being selected.

Principle of inertia of large numbers

Principles of Sampling

• It is based upon the concept that as the sample size increases the better results we will get. For example if we have to study the weight of the students studying in a college then fairly adequate sample of the students help us to arrive at good results.

Principle of Validity

Principles of Sampling

• if valid tests are derived only then sampling design is termed as valid.

Principle of Optimization

Principle of Sampling

• this principle states that with the help of sample one must be able to get optimum results with maximum efficiency and minimum cost.

Sample

• A subgroups of the members of population chosen to participate in the study.

• Only a handful of units of population

• It focus on making interferences about population.

• Data collection is sampling survey or sampling.

Population

• Refers to collection of all elements possessing common characteristics that comprise the universe.

• Each and every unit of the group

• It focus on identifying the characteristics

• Data collection is complete enumeration or census

Data

Is any facts, observations, or information collected together for reference or analysis which is used as a basis for decision making.

Variable

• Any characteristic which changes its values.

• Examples: height, weight, sex, marital status, eye color.

• It can be classified as Qualitative or Quantitative.

Constant

• A characteristic which does not changes its value or nature.

• Example: height of a person after 25 years of age.

Types of Variables

1. Dependent

2. Independent

3. Confounding

Dependent Variable

• A variable that depends on other variables.

  • Outcome

  • Predicted

Independent Variable

• Variables that does not depend on other variables.

  • Explanatory

  • Predictor

  • Risk Factor

  • Influencing Factor

Confounding Variable

• Variable/s that correlates (directly or indirectly) with both the independent variable and dependent.

  • Nuisance variable

  • Interfering variable

  • Covariate

Two types of data

1. Qualitative Data

2. Quantitative Data

Qualitative Data

• It is non numerical data that can be arranged into categories.

• This data is also called as Categorical data.

  • Examples: gender of an individual, nationality of a player grade in examination.

Quantitative Data

• It is a numerical data that consists of counts or measurements.

  • Examples: weight of person, examination marks, profit of a salesman.

Categorical

1. Nominal ( No Order)

   • Dichotomous, binary, binomial

   • Polychotomous

2. Ordinal (Ordered)

• Answers “what?”

• Qualitative data is categorized

Numerical

1. Continuous

   • Interval

   • Ratio

• Answers “how many?”

• Quantitative data is measured

Discrete and continuous

Quantitative data can further be classified as?

Discrete data

• Takes on only a finite or countable number of values. These are usually whole numbers.

• Examples: population of a country, number of cases of certain disease, number of student in a class.

Continuous Data

• Takes all possible values in a certain range and thus have an infinite number of values. This data does not contain any gaps, breaks or jumps.

• Examples: height of a person, temperature at a certain place, agricultural production.

Binomial Data

• This type of data has only two possible outcomes in each trial, like yes/no, success/failure, or win/lose. Think of it as a choice between two distinct options.

  • Example: When you toss a coin, it lands on either Heads or Tails. There’s no middle ground or other option – just two possible results.

Polychotomous Data

• This data type has more than two categories, but there’s no specific order among the options. It’s like choosing from a list where each option is distinct but equal in rank.

  • Example: Choosing a favorite fruit: Apple, Banana, Orange, Grape. Each fruit is a separate choice, and none is ranked above the other.

Ordinal Data

• This data type has a clear order or ranking among the categories, but the spacing between the levels isn’t equal. It’s like a ladder where each rung represents a different level, but the distance between them isn’t fixed.

  • Example: Rating a product on a scale like Poor, Fair, Good, Very Good, Excellent. These ratings show a progression, but you can’t say the difference between “Good” and “Very Good” is the same as between “Fair” and “Good.”

Interval Data

• Has equal spacing between values, meaning the difference between units is consistent. However, interval data doesn’t have a true zero – zero is just another point on the scale, not an absence of what’s being measured.

  • Example: Temperature in Celsius: 0°C, 10°C, 20°C. Each interval (10°C) is equal, but 0°C doesn’t mean “no temperature” – it’s just another point on the scale.

Ratio Data

• Has equal intervals and a true zero, meaning zero signifies the absence of what’s being measured. This allows for direct comparisons, like saying something is “twice as much.”

  • Example: Height: 0 cm, 50 cm, 100 cm. Here, 0 cm means no height (true zero), and you can say 100 cm is twice as tall as 50 cm.

Principals of data presentation

1. To arrange the data in such a way that it should create interest in the reader's mind at the first sight.

2. To present the information in a compact and concise form without losing important details.

3. To present the data in a simple form so as to draw the conclusion directly by viewing at the data.

4. To present it in such away that it can help in further statistical analysis.

Tabular, Graphical

Two types of presentation of data

Simple, complex

Two types of tabular

Graphical for quantitative data

Presentation of data includes:

1. Histogram

2. Frequency polygon

3. Frequency curve

4. Line chart

5. Normal distribution curve

6. Cumulative distribution curve

7. Scatter diagram

Graphical for qualitative data

Presentation of data includes:

1. Bar chart

2. Pictogram

3. Pie chart

4. Map diagram

Simple Tables

Double Table

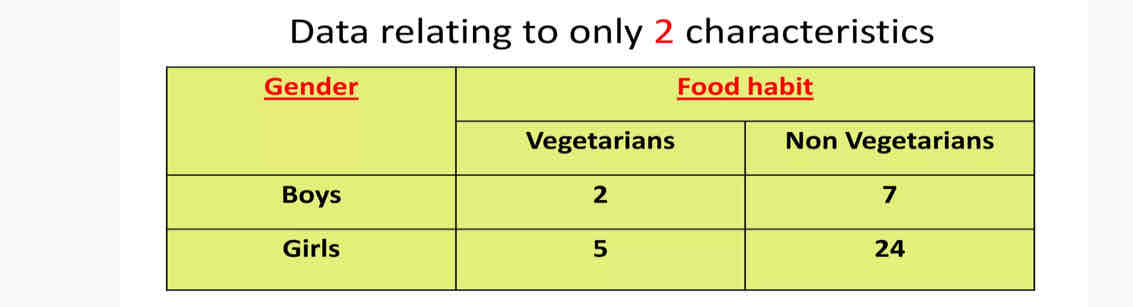
Triple Table

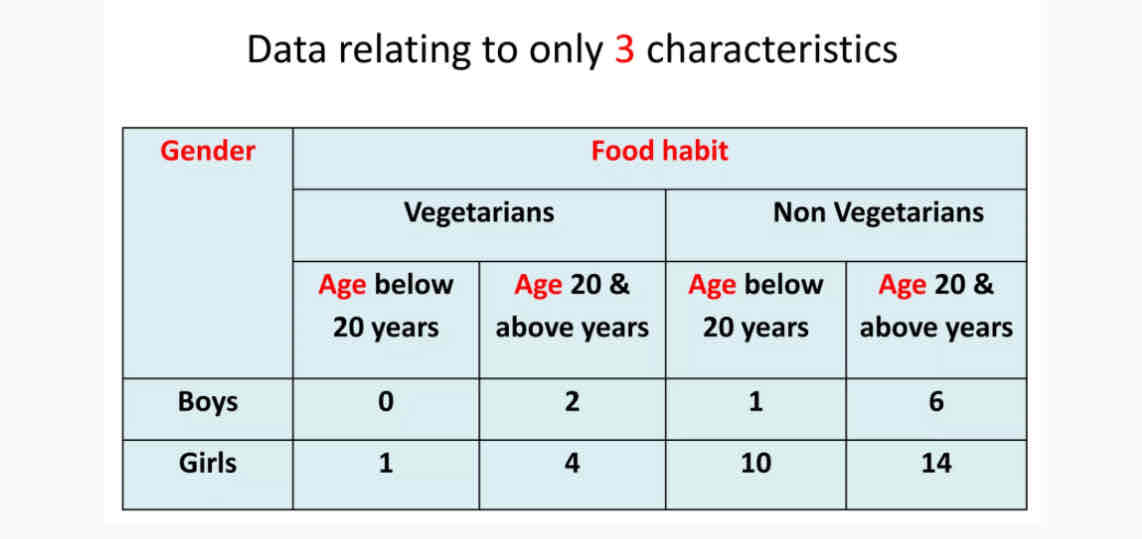
Pointers to remember for tables

Graphs and charts

• Rapid grasp of data

• Visually attractive

• Tells more in less

Common types of graphs

1. Histogram

2. Line graph

Graphs

Its use is for plotting quantitative data using a coordinate system.

Histogram

Graphs

• Used for presenting frequency distrubution

Line graph

Graph

• Used to present more than one set of data in terms of frequency distribution

• are used to display the comparison between two variables which are plotted on the X-axis and Y-axis.

• They organize and present data in a clear manner and show relationships between the data.

• displays a change in direction.

• It shows trend of an event occurring over a period of time to know whether it is increased or decreased. Eg: IMR, Cancer deaths etc.

Time, quantity

In Line graph, the X-axis represents measures of _____, while the Y-axis represents percentage or measures of ____.

Line Diagram

• Are used to show the trend of events with the passage of time.

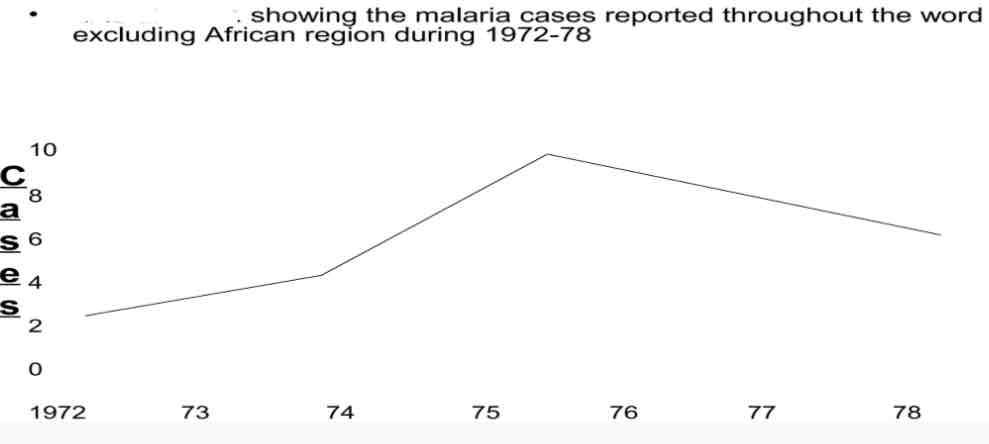
Charts

• For plotting qualitative data using only one coordinate.

Common types of charts

1. Bar charts

2. Pie charts

Bar chart

Charts

• Used to compare categories or groups

Pie chart

Charts

• Used to illustrate the division of the whole into segments or sections

Pointers to remember for graph and charts

Statistical map or dot map

• When statistical data refers to geographic or administrative areas, it is presented either as ________.

• The shaded maps are used to present data of varying size. The areas are shaded with different colour or different intensities of the same colour, which is indicated in the key.

Scatter diagram

• Show the relationship between the two variables.

  • e.g a positive correlation/ association between the intake of fat and sugar in the average diets of 41 countries.

• If the dots cluster round a straight line, it shows evidence of a relationship of a linear nature.

• If there is no such cluster, it is probable that there is no relationship between the variables.