BAZA CIAŁA STAŁE
1/53
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
54 Terms

wybrać podstawowy układ odniesienia i podzielić ciało na n ciał o elementarnych kształtach. Wyznaczyć położenia środków ciężkości elementarnych ciał w pomocniczych układach współrzędnych. Wyznaczyć położenia środków ciężkości elementarnych w podstawowym układzie współrzednych. Wyznaczyć współrzędne położenia środka ciężkosci ciała

odp:B

naprężenie początkowe i czas relaksacji
S(t) = So * e^(-t/fi)

M0=r x P
|M0| = P * h
P to siła, r to promien

prawo hooke’a

różny od zera, równy zero, różny od zera

zależy od typu materiału, miejsca pobrania próbki, temperatury i prędkości odkształcenia

3 6 15

Energii sprężystej
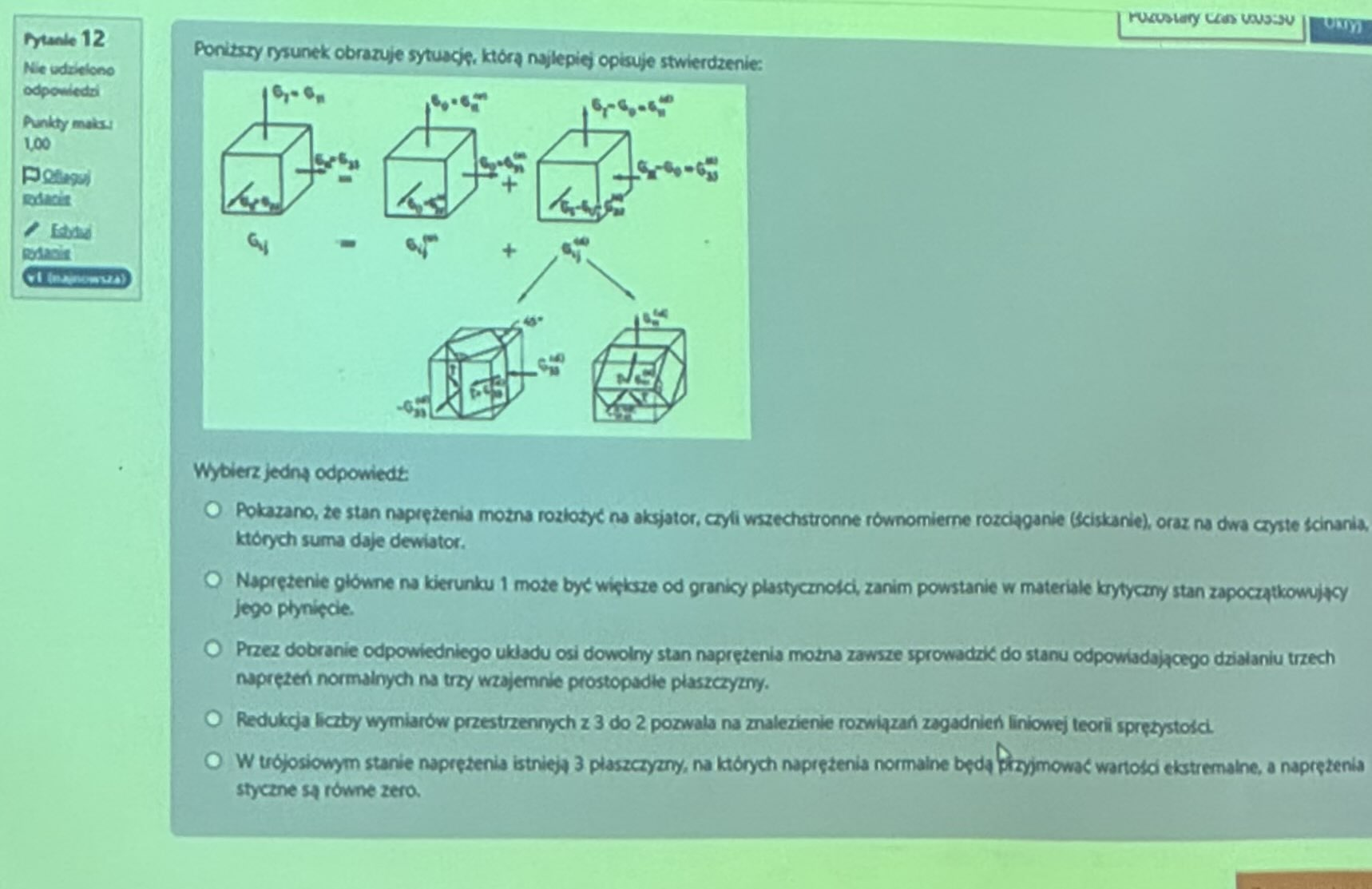
Pokazano, że stan naprężenia można rozłożyć na aksjator, czyli wszechstronne równomierne rozciąganie(ściskanie), oraz na dwa czyste ścinania, których suma daje dewiator
15 15

M= P*a, przy czym moment pary sił to wektor, którego wartość bezwzględna (moduł) równa jest iloczynowi wartości liczbowej jednej z sił pary oraz ramienia tej pary
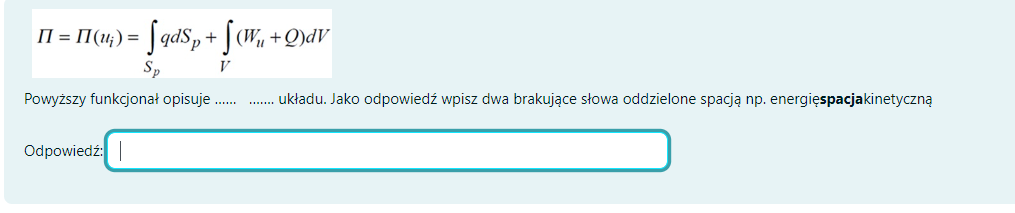
energię potencjalną
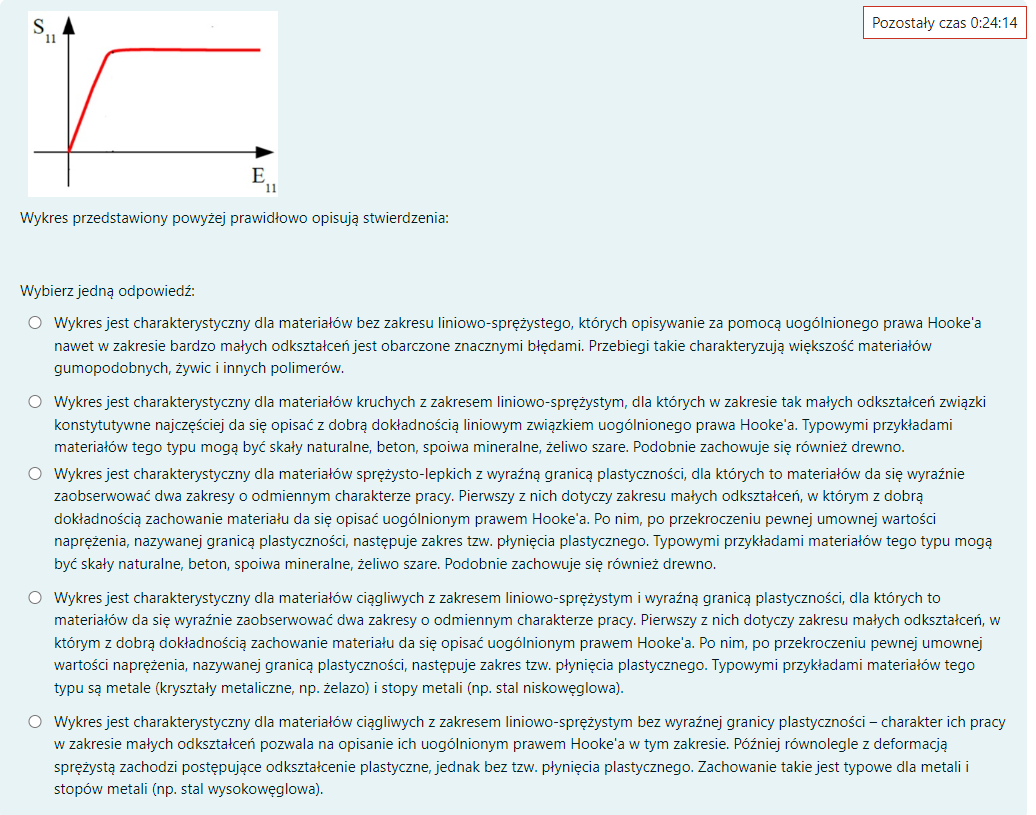
Wykres jest charakterystyczny dla materiałów ciągliwych z zakresem liniowo sprężystym i wyraźną granicą plastyczności, dla których to materiałów da się wyraźnie zaobserwować dwa zakresy o odmiennym charakterze pracy. Pierwszy z nich dotyczy zakresu małych odkształceń, w którym z dobrą dokładnością zachowanie materiału da się opisać uogólnionym prawem Hookea. Po nim po przekroczeniu pewnej umowenej wartości naprężenia, nazywanej granicą plastyczności, następuje zakres tzw. płynięcia plastycznego. Typowymi przykładami materiałów tego typu są metale ( kryształy metaliczne, np. żelazo) i stopy metali(stal niskowęglowa)

pełzania

Clapeyrona
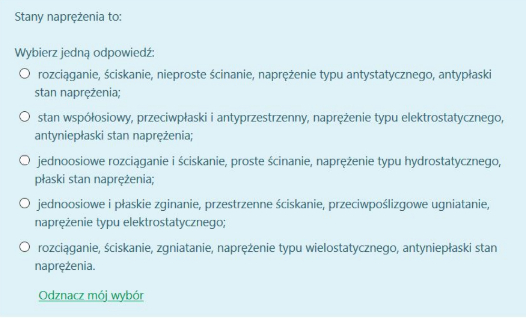
jednoosiowe rozciąganie i ściskanie, proste ścinanie, naprężenie typu hydrostatycznego, płaski stan naprężenia

Wybrać podstawowy układ odniesienia i podzielić ciało na n ciał o elementarnych kształtach. Wyznaczyć ciężary i położenia środków ciężkości elementarnych ciał w pomocniczych układach współrzędnych. Wyznaczyć położenia środków ciężkości elementarnych ciał w podstawowym układzie współrzędnych. Wyznaczyć współrzędne położenia środka ciężkości ciała

Huber’a, największych naprężeń normalnych, największych naprężeń tnących, największego wydłużenia względnego

Jest prostopadły do płaszczyzny działania obu sił. Jest niezależny od wyboru punktu 0 i jest wielkością stałą, a jego wartość równa jest iloczynowi wartości jednej z sił pary i odległości między siłami. Jest wektorem swobodnym. Układ par leżących w jednej płaszczyźnie jest równoważny jednej parze sił, której moment równa się sumie momentów par.

zero, różny od zera, różny od zera (bo to drugi czyli wyznaczniki)
Jakiego zjawiska nie może ująć model Kelvina-Vogta?
Model Kelvina-Vogta nie moze ująć zjawiska relaksacji!!!

Moment siły względem punktu leżącego na linii jej działania równy jest zero. Wartość momentu siły względem punktu równa się iloczynowi wartości siły i odległości punktu od linii działania siły. Moment siły względem punktu 0 nie zmieni się jeżeli siłę przesuniemy dowolnie wzdłuż jej linii działania. Podstawową jednostką momentu jest Nm

normalne, styczne, główne, zredukowane, uogólnione, intensywność naprężenia, własne, rzeczywiste i inżynierskie

Greena, Almansiego, Cauchyego, intensywność odkształcenia, liniowe, kątowe, względne, bezwzględne, logarytmiczne, całkowite, cząstkowe, inżynierskie

prostoliniowy prostokątny(kartezjański), walcowy(cylindryczny), kulisty(sferyczny), elipsoidalny, stożkowy, hiperboloidalny(jebac hipopotamy)

Jest prostopadły do płaszczyzny działania obu sił. Jest niezależny od wyboru punktu 0 i jest wielkością stałą a jego wartość równa jest iloczynowi wartości jednej z sił pary i odległości miedzy siłami. Jest wektorem swobodnym. Układ par leżących w jednej płaszczyznie jest równoważny jednej parze sił, której moment równa się sumie momentów par.

Stan odkształcenia jest stanem płaskim, a stan naprężenia jest stanem antypłaskim. Rozkład naprężeń, odkształceń i przemieszczeń wzdłuż kierunku Z jest stał. Obciążenie musi być obciążeniem płaskim, leżącym w płaszczyźnie (X;Y). Ciało nie ma możliwości deformacji w kierunku Z. Ten stan występuje w wycinkach ciał sprężystych, w których jeden z wymiarów jest znacznie większy od pozostałych
Kiedy stan naprężenia jest stanem płaskim?
"Stan naprężenia jest stanem płaskim, a stan odkształcenia jest stanem antypłaskim. Rozkład naprężeń, odkształceń i przemieszczeń wzdłuż kierunku Z jest stały. Obciążenie musi być obciążeniem płaskim, leżącym w płaszczyźnie (X;Y). Ciało musi mieć swobodę deformacji w kierunku Z. Ten stan występuje w cienkich tarczach i powłokach, w których jeden z wymiarów jest znacznie mniejszy od pozostałych.

modelu ciała, modelu połączeń bezpośrednich, modelu połączeń pośrednich, modelu oddziaływań zewnętrznych, modelu obciążeń
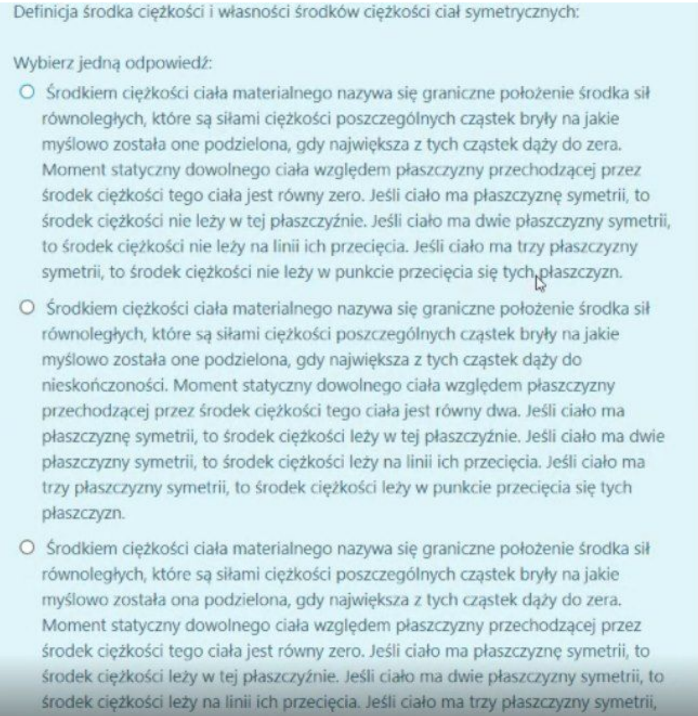
środek ciężkości musi dążyć do zera, jak ma jedna plaszczyzne symetrii to srodek leczy w tej plaszczyznie, jak dwie to na linni ich przeciecia, jak trzy to w punkcie przeciecia tych plaszczyzn

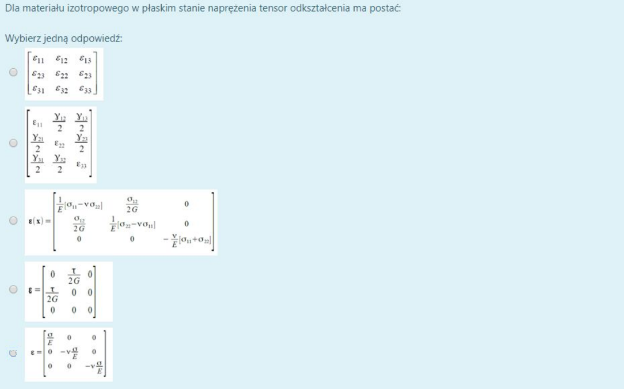
w pierwszej postaci występuje zależność naprężeń od odkształceń wyrażona za pomocą stałych(pierwszy i drugi parametr Lamego) W drugiej postaci wystepuje zależność odkształceń od naprężeń wyrażona przez stałe (Moduł Younga, Kirchoffa i wspolczynnik Poissonea). W trzeciej postaci wystepuje moduł sztywności objętościowej i poprzecznej




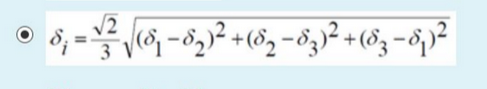
Wzory na intensywność naprezenia, intensywnosc odkształcen i jakas inna intensywnosc odksztalcen

WYMYŚLONE PRZEZ CHATA W OPARCIU O WYKŁADY
"Dla ogólnego (niegłównego) stanu odkształceń intensywność odkształcenia wyrażona przez odkształcenia liniowe (l) i kątowe (l_xy) wynosi:"
Możliwe odpowiedzi:
a) δ₀ = (1/3) * (δ₁ + δ₂ + δ₃)
b) ε = ln(L₁ / L₀)
c) I_H = (√2 / 3) √[ (l₁₁ - l₂₂)² + (l₂₂ - l₃₃)² + (l₃₃ - l₁₁)² + 6 (l₁₂² + l₂₃² + l₃₁²) ]
d) δᵢ = (√2 / 3) * √[ (δ₁ - δ₂)² + (δ₂ - δ₃)² + (δ₃ - δ₁)² ]
odp:C

odp: D
B odpada bo to jest wzór na naprężenie zredukowane dla OGÓLNEGO, trójwymiarowego stanu naprężeń.


składowych tensora odkształcenia, przemieszczenia na kierunku działania obciążenia i błędów pomiarowych
(nie było tego na prezkach dla naszego rocznika)

Bragga
(tez nie bylo na prezkach w tym roku)

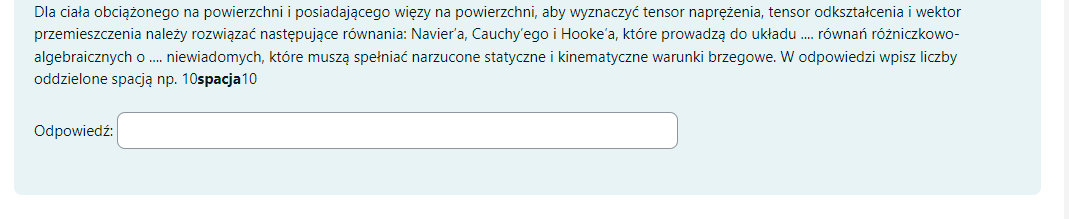
Równania równowagi z uwzględnieniem statycznych warunków brzegowych, równania Cauchy'ego z uwzględnieniem kinematycznych warunków brzegowych, równania Hooke'a, co prowadzi do 15 równań o 15 niewiadomych;

według ai studio: tarcie, temperatura, prędkość odkształcenia;

Jest taki sam, w każdym punkcie ciała i wyraża zależność stanu naprężenia od stanu odkształcenia, a wybór postaci tej zależności musi spełniać zasady determinizmu, lokalności i obiektywności materialnej.

ciągliwych z zakresem liniowo-sprężystym, a także kruchych w zakresie małych odkształceń;

odp: B

sprężyny (materiał idealnie sprężysty), tłumika (materiał idealnie lepki) i suwaka (materiał idealnie plastyczny);

odp:D


von Misesa i największych naprężeń tnących (Tresci);

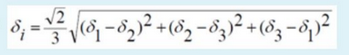

Hookea

minimalną
![<p>[PYTANIE WYMYŚLONE Z CHATEM]<br><br>czy widać tutaj granice plastyczności?</p>](https://knowt-user-attachments.s3.amazonaws.com/d2c4f634-0131-4413-baeb-850b03e59d08.png)
[PYTANIE WYMYŚLONE Z CHATEM]
czy widać tutaj granice plastyczności?
Tak, na tym wykresie jest bardzo wyraźnie widoczna granica plastyczności.
Dokładniej rzecz ujmując, widać tu nawet dwie granice plastyczności:
Górna granica plastyczności: To ten pierwszy, najwyższy "ząbek" na końcu prostej linii. To jest moment, w którym materiał po raz pierwszy "poddaje się" i zaczyna płynąć.
Dolna granica plastyczności (oznaczona jako Rₚ): Po pierwszym "poddaniu się", naprężenie lekko spada i przez pewien czas materiał płynie przy niższym, prawie stałym naprężeniu. Ten "zygzakowaty" lub pofalowany odcinek to właśnie wyraźna granica plastyczności.
W skrócie:
Ten wykres jest podręcznikowym przykładem zachowania stali niskowęglowej, która charakteryzuje się właśnie takim zjawiskiem – bardzo wyraźną, "ząbkowaną" granicą plastyczności, po której następuje dalsze umocnienie (wzrost naprężenia z odkształceniem) aż do osiągnięcia maksymalnej wytrzymałości (Rm).
statyczne momenty bezwładności wzór
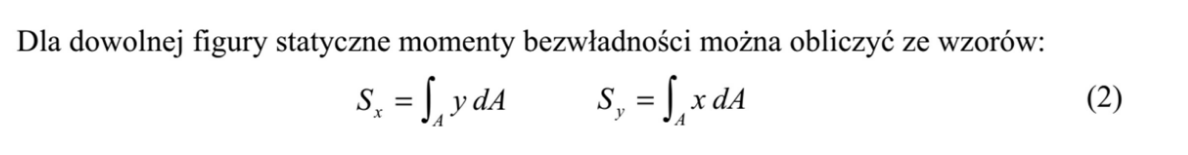

Bragga