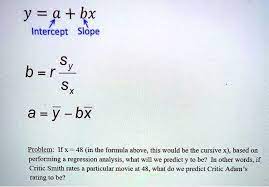Chapter 3:3.2 Least Squares Regression Line

Regression line

1) linear relationships between 2 quantitative variables

2) one of the variables helps explain or predict the other

• ex: predict the value of y for a given value of x

Equation of a regression line

ŷ= a + bx

ŷ meaning in ŷ= a + bx

y hat, the predicted value of the response variable

a meaning in ŷ= a + bx

y intercept, the predicted value of y when x = 0

b meaning in ŷ= a + bx

slope, amount by which y is predicted to change when x increases by 1 unit

Extrapolation

don’t make predictions using values of x that are much larger or smaller than those present in data

Residual

difference between an observed value of the response variable and the value predicted by the regression line

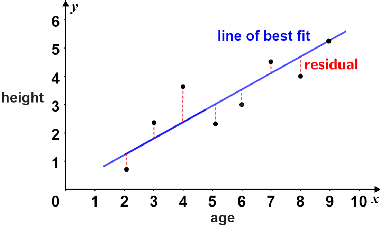
Residual formula

y - ŷ or observed y - predicted y

What does it mean if the residual is positive?

y value is c more that expected value

What does it mean if the residual is neg?

y value is c less than expected value

Standard deviation of the Residuals

measures typical distance between the actual y values and the predicted y values

Standard deviation of the residuals formula

see picture

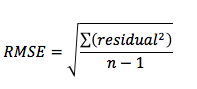
Least squares regression line

regression line that minimizes the sum of the squared residuals

Residual plots

scatterplot of the residuals against the explanatory variable

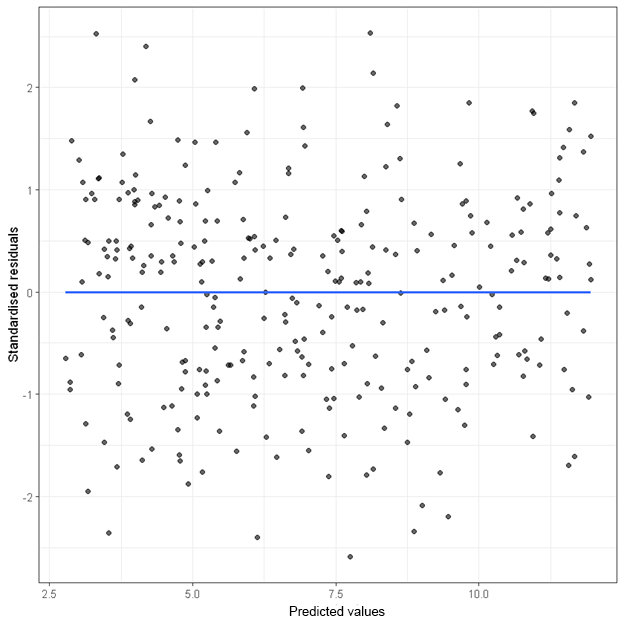
Residual plots should have…..

no obvious pattern left over

Coefficient of Determination r²

measures the % of the variability in the response variable that is accounted for by the least squares regression line

r² equation

see picture

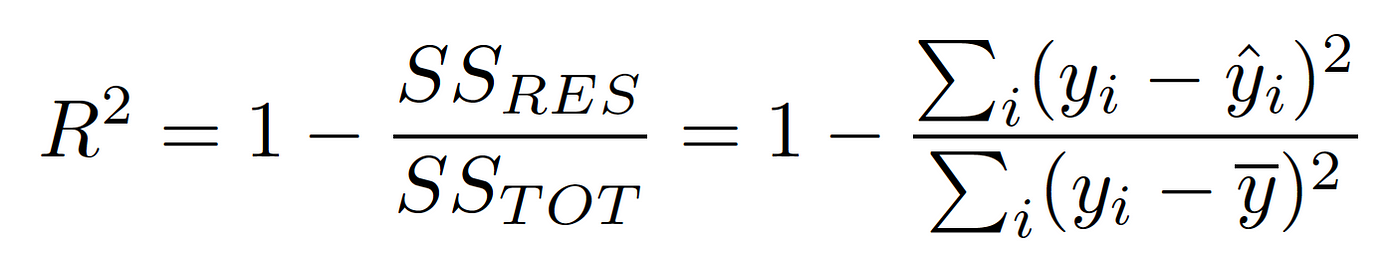
How to find regression line from mean

1) b = r(s_y/s_x)

2) a = ȳ - bx̄