chapter 16: relative motion anaylsis: velocity AND acceleration

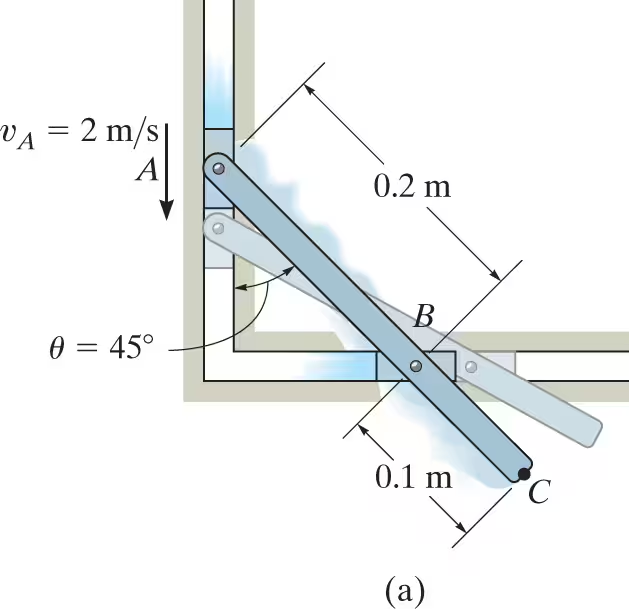
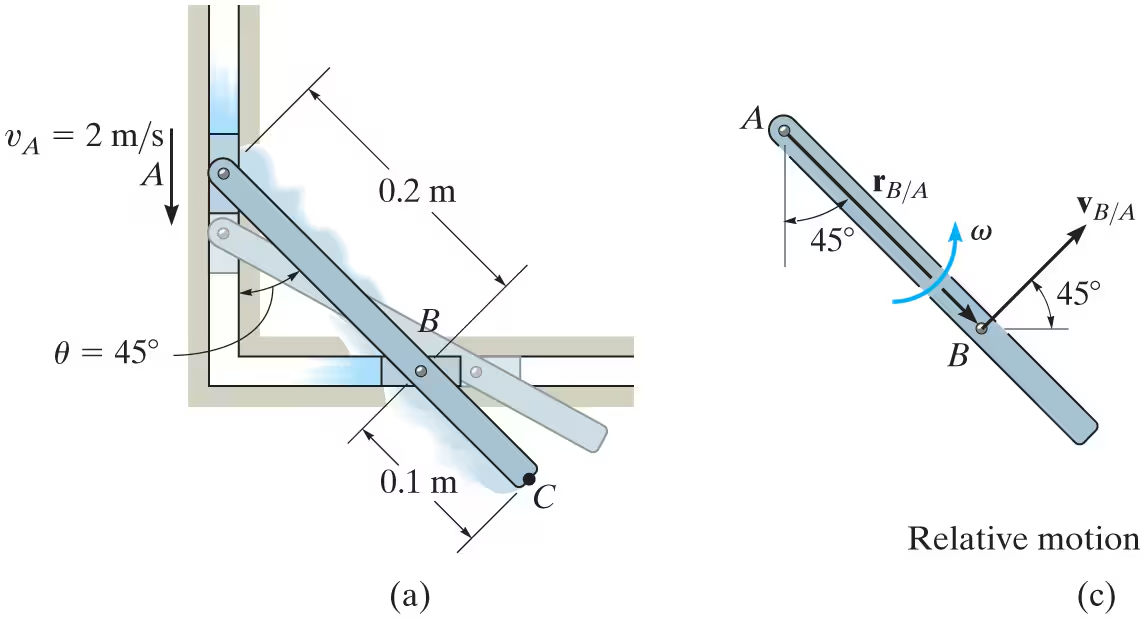
The link shown in Fig. 16–14a is guided by two blocks at A and B, which move in the fixed slots. If the velocity of A is  2 m/s downward, determine the velocity of B at the instant θ=45°.

vB=vA+vB/A

-vB moves horizontally to the right

-vA moves vertically down

-vB/A moves in a circular path, so use rw and define angle.

vB/A= w(.2) at a 45 degree angle up and to the right

use vx=0 and vy=0

solve

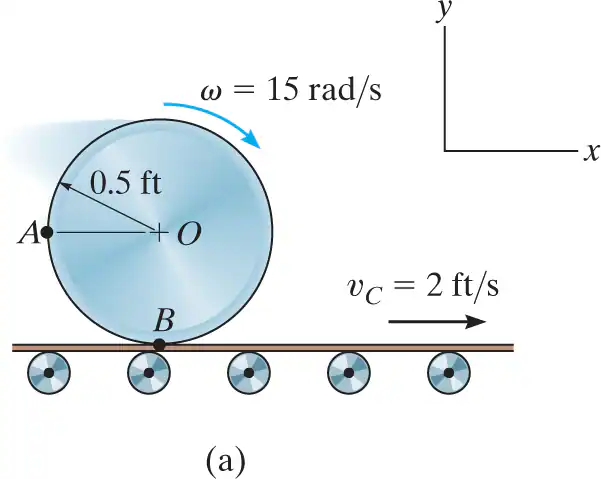
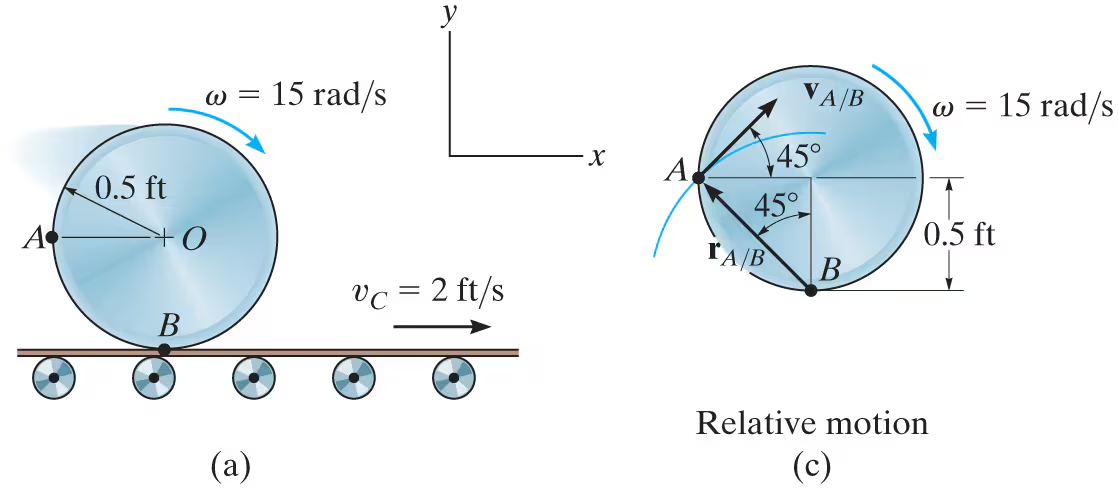
The cylinder shown in Fig. 16–15a rolls without slipping on the surface of a conveyor belt which is moving at  2 ft/s. Determine the velocity of point A. The cylinder has a clockwise angular velocity  ω=15 rad/s at the instant shown.

-vA=vB+vA/B

-vA/B=wrA/B = 15(.5/cos45)

-vA=vB+vA/B

= v(A)x > + vAy^ = 2ft/s + 10.6 at an angle of 45 up and right

resolve into x and y and solve

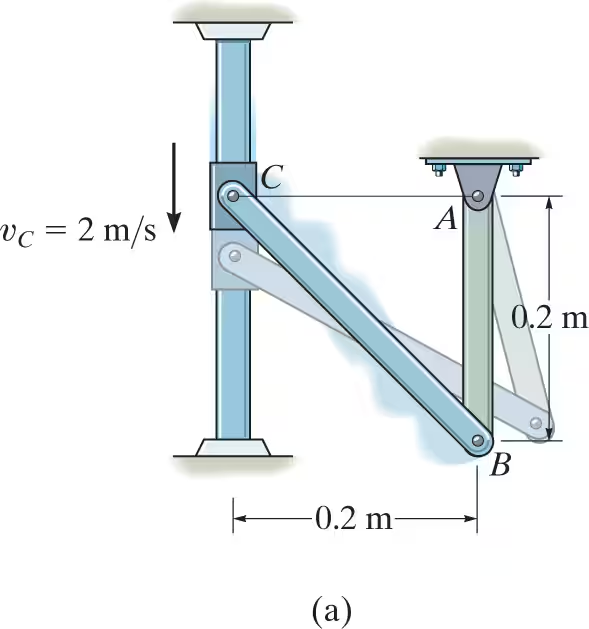
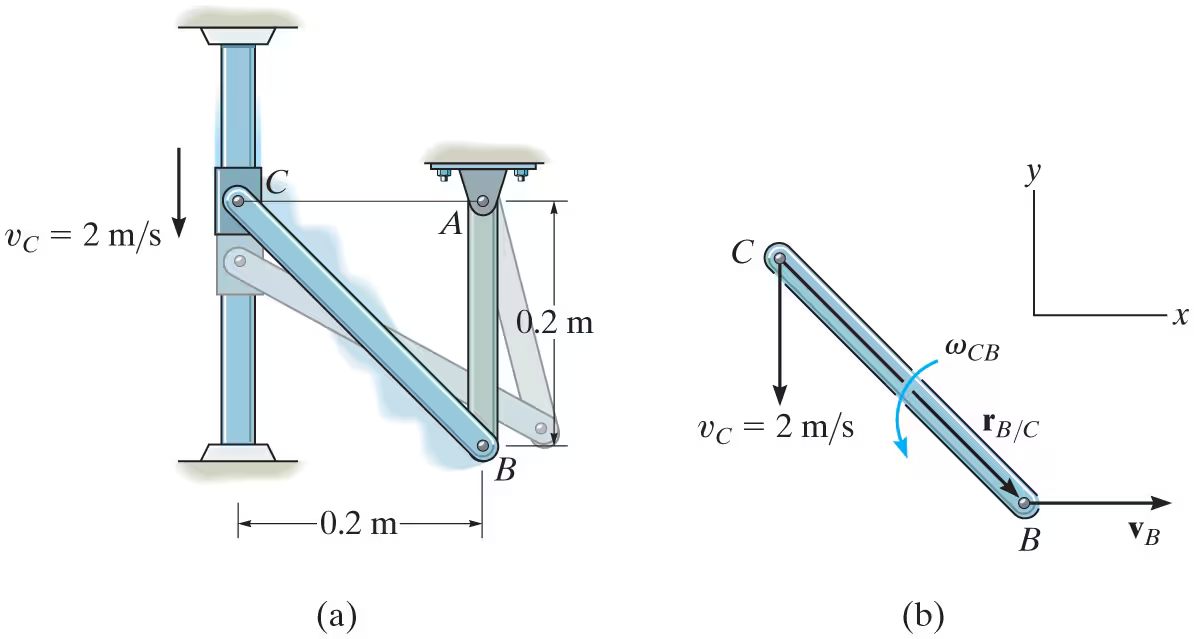
The collar C in Fig. 16–16a is moving downward with a velocity of  2 m/s. Determine the angular velocity of CB at this instant

-vB=vC+vB/C

= vB > = 2m/s down + wCB(.2root(2)m) at an angle of 45 up to the right

resolve into x and y

solve

ya

yAA