L4_Training deep neural networks

Flashcards covering the key concepts from the lecture on training deep neural networks, including parameters, activation functions, backpropagation, gradient descent, and regularization techniques.

What is the simple formulation of a machine learning model?

y^ = f(x, θ) where y^ is the prediction, x is a data point, and θ are parameters of the model. This maps inputs to outputs based on adjustable parameters.

Analogy: Think of f as a recipe, x as the ingredients, and θ as the adjustable settings. We tweak θ to get the desired y^ (the dish).

What are the parameters of a simple fully-connected neural network?

One weight per connection (line) and one bias term per node (circle). Weights scale inputs, biases shift activation thresholds.

Analogy: Weights are like the strength of a connection between neurons, and bias is a threshold that needs to be overcome for a neuron to activate.

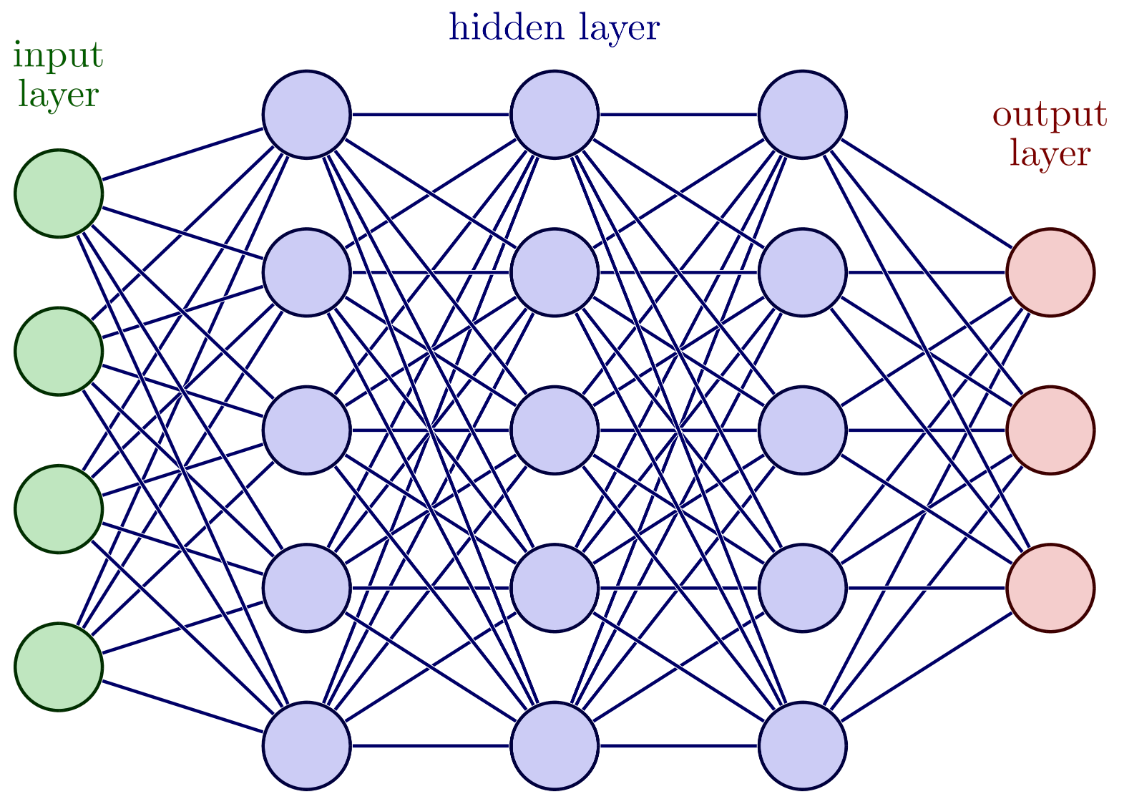
What separates a neural network from standard linear regression?

The non-linear activation function. It introduces non-linearity, enabling the network to learn complex relationships.

Analogy: It's like a switch that isn't just 'on' or 'off,' but something in between, allowing complex combinations.

What defines a good activation function?

1. Nonlinear: The activation function should introduce non-linearity into the network, allowing it to learn and represent complex patterns and relationships in the data.

2. Differentiable: The activation function should be smooth and differentiable, enabling the use of gradient-based optimization methods like backpropagation.

3. Switches from Off for Negative Inputs to On for Positive Inputs: The activation function should have a clear distinction between active and inactive states, which helps in learning meaningful features.

The properties dictate model learning capabilities.

Analogy: Think of an activation function as a decision maker that needs to be both adaptable and decisive to solve complex problems, by making the system non linear.

What activation function is used in the final layer for Regression tasks?

No activation (linear activation) with output range (-∞, ∞). The final layer is typically a linear layer. This allows the network to output a continuous range of values, suitable for regression tasks.

Analogy: The raw ingredients don't get altered. Used for predicting any real number.

What activation function is used in the final layer for Binary classification tasks?

Sigmoid with output range [0, 1]. It converts the output to a probability, useful for binary classification.

Analogy: Squashes the output to a probability between 0 and 1, perfect for yes/no situations.

What activation function is used in the final layer for Multiclass classification tasks?

The Softmax function transforms the raw output scores (logits) of a neural network into a probability distribution over multiple classes. This means that each output value is between 0 and 1, and all the output values sum to 1, representing the network's confidence in each class. It converts raw scores into probabilities for multiclass classification.

Analogy: Like normalizing votes; it turns raw scores into probabilities that sum to one, indicating class likelihood.

What is the solution for optimizing the parameters of a large neural network efficiently?

Backpropagation: is a method used to train neural networks. It calculates how much each part of the network contributed to the error and then adjusts the network's parameters to reduce the error. This process relies on the network's output being differentiable, meaning we can measure how changes in the parameters affect the output. It's an algorithm for efficiently computing gradients in neural networks. Analogy: Like figuring out which ingredient is making the cake taste bad by tracing back the recipe.

What is step 1 of Backpropagation?

Randomly initialize parameters, Run a forward pass on a mini-batch and keep track of the output for each node. Begin by setting the initial state with random parameter estimates and make sure to record what happens during each pass.

Analogy: Start with a guess, see how the cake turns out, and keep notes on each step.

What is step 2 of Backpropagation?

Compute the Loss/error, which measures how big the error is. A loss function quantifies the difference between predictions and actual values. This step quantifies the error from forward pass.

Analogy: Measure how far your cake is from the target taste/quality.

What is step 3 of Backpropagation?

Compute how much each parameter contributed to the loss (compute the gradient for each parameter), starts at the last layer and moves backwards (backwards pass). Compute the gradient of parameters beginning from the last to first layer.

Analogy: Pinpoint which adjustments to the recipe would most improve the cake, starting from the taste-testing stage.

What is step 4 of Backpropagation?

Run one step of gradient descent to find better values for all parameters. Updates parameters using the computed gradients. Adjust the parameters by using the gradient descent algorithm.

Analogy: Adjust the recipe based on the gradient to make the cake taste better next time.

What is the main idea behind Gradient Descent?

The gradient points towards the direction of maximum increase of the loss function. We want to find the minimum, so need the negative gradient. Optimization algorithm that iteratively adjusts parameters towards the minimum of the loss function. Adjust parameters towards the minimum of the loss function

Analogy: If the gradient indicates 'more salt makes it worse', we need to 'add less salt'.

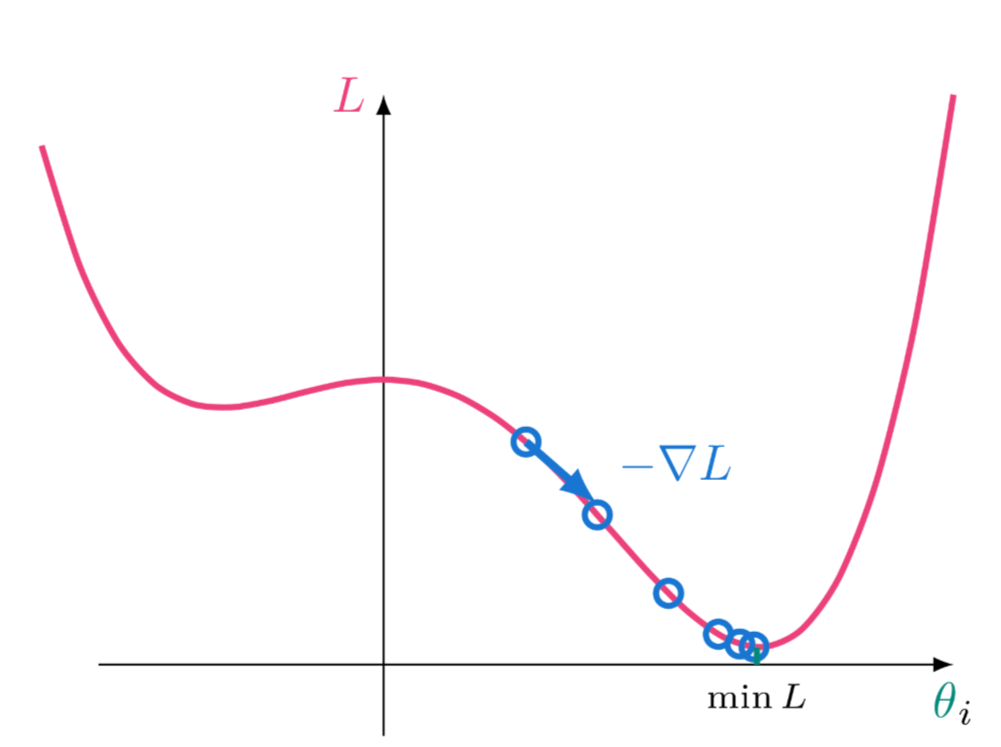
How does the gradient get used in gradient descent?

With the gradient in place, we take steps downward (along the negative gradient), towards the optimal solution. Iteratively updating parameters in the direction opposite to the gradient. Update the parameters iteratively to find the optimal weights.

Analogy: Following the 'less salt' direction until the cake tastes just right.

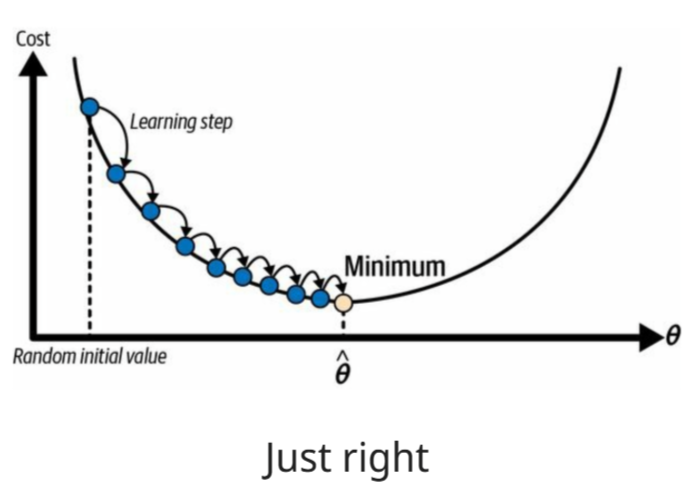
What is the learning rate?

A hyperparameter determining the proper 'step size'. Too small causes slow convergence, to large causes no convergence. It's a scalar that controls the magnitude of parameter updates.

Analogy: How big of an adjustment to make to the recipe at each step. Too little, you'll never reach the right taste; too much, you'll overshoot.

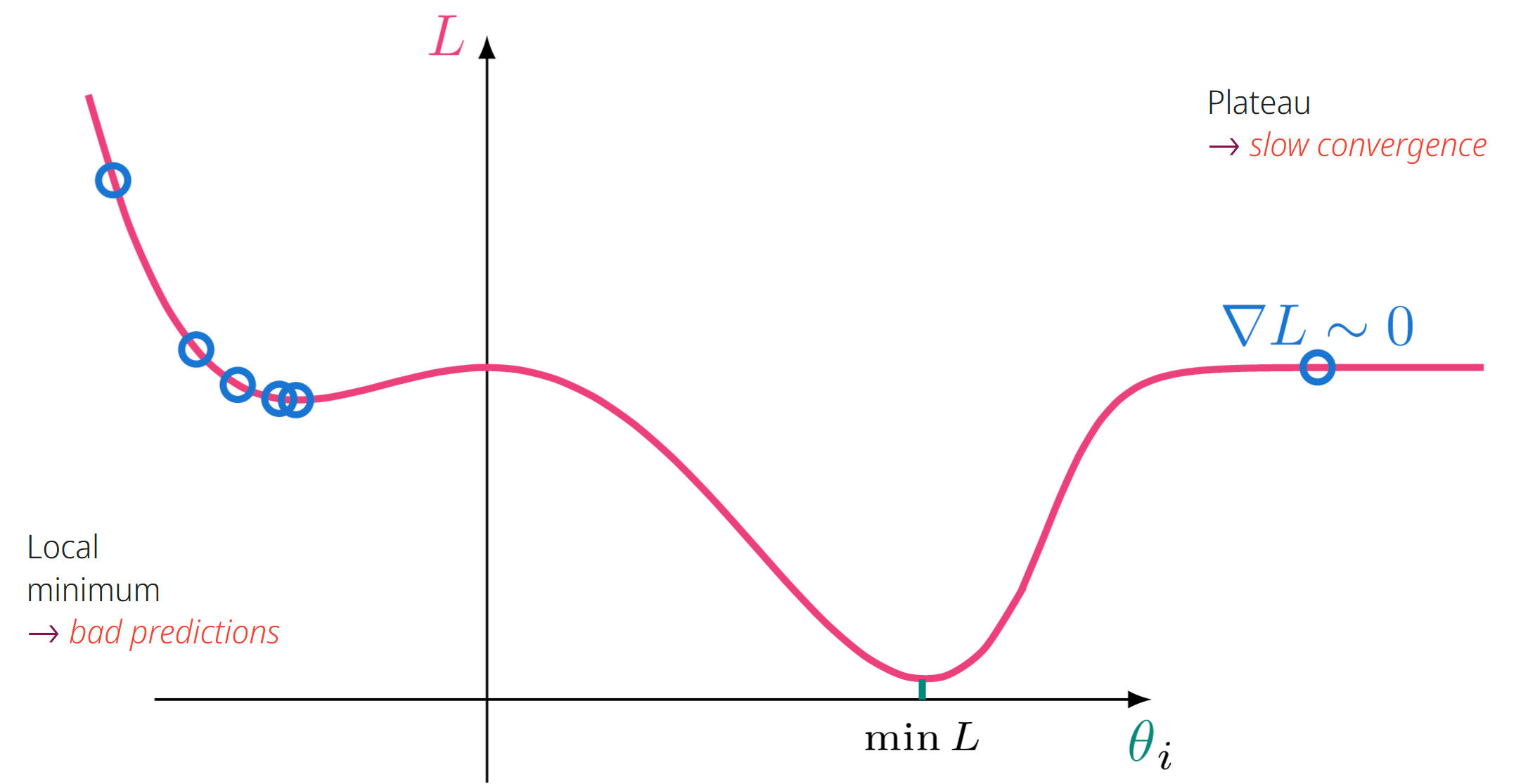
What are two practical problems commonly encountered during optimization?

Local minimum and Plateaus- bad predictions, and slow convergence, respectively. These are challenges in optimization landscapes that impede convergence to the global minimum.

Analogy: Getting stuck in a 'good enough' but not 'best' taste, or parts of the cake that just don't change no matter what you do.

What gradient amplification effects can affect training?

Vanishing and Exploding Gradients. These refer to gradients becoming extremely small or large during backpropagation.

• Vanishing Gradients: Gradients become extremely small, approaching zero. This prevents the weights from being updated effectively during training, leading to the network learning very slowly or not at all in certain layers. The earlier layers of deep networks are particularly susceptible.

• Exploding Gradients: Gradients become extremely large, causing the weights to update excessively. This can lead to unstable training, where the model oscillates wildly and fails to converge.

Analogy: Imagine the flavor changes become incredibly subtle (vanishing) or overly strong (exploding) as you adjust the recipe. Both extremes prevent you from perfecting the dish.

What is a vanishing gradient?

Gradients go towards zero resulting in NO learning. This occurs when gradients become too small to update parameters effectively.

Analogy: The flavor stops changing no matter what you adjust in the recipe. No-one can tell the difference.

What is an exploding gradient?

Gradients go towards infinity resulting in NO learning. This occurs when gradients become too large, destabilizing training.

Analogy: The flavors explode so much that it ruins the entire cake. All adjustment is too much to the point it no longer resembles cake.

What are common approaches to avoid vanishing/exploding gradients?

Choose a non-saturating activation function (like ReLU), initialize each layer’s parameters according to the number of input and output connections, and add normalisation layers to the model. These methods help maintain stable gradients during training.

Analogy: Select reliable ingredients, measure quantities precisely, and ensure flavors blend well.

What activation functions are typically applied alongside which initialization methods?

Glorot (None, tanh, sigmoid, softmax)

He (Kaiming) (ReLU, GELU, Swish).

These are initialization strategies designed to work well with specific activation functions, alleviating vanishing/exploding gradients.

Analogy: Certain activation functions perform better with certain initialization techniques. Knowing which goes together is key to good results.

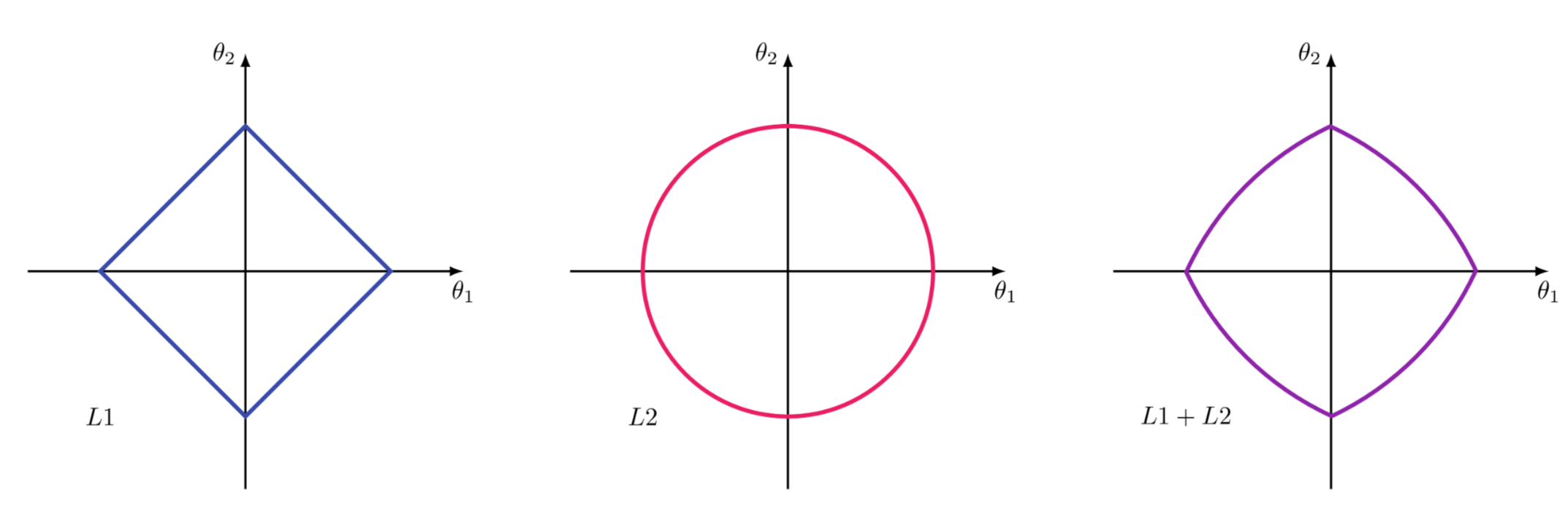
What regularization can be applied to neural network nodes?

L1 and L2 Regularization. L1 adds the absolute values of the weights to the loss function, while L2 adds the squared values.

Analogy: Like adding constraints to the recipe such as calorie limits or ingredient restrictions, to ensure a 'healthier' outcome (less overfitting).

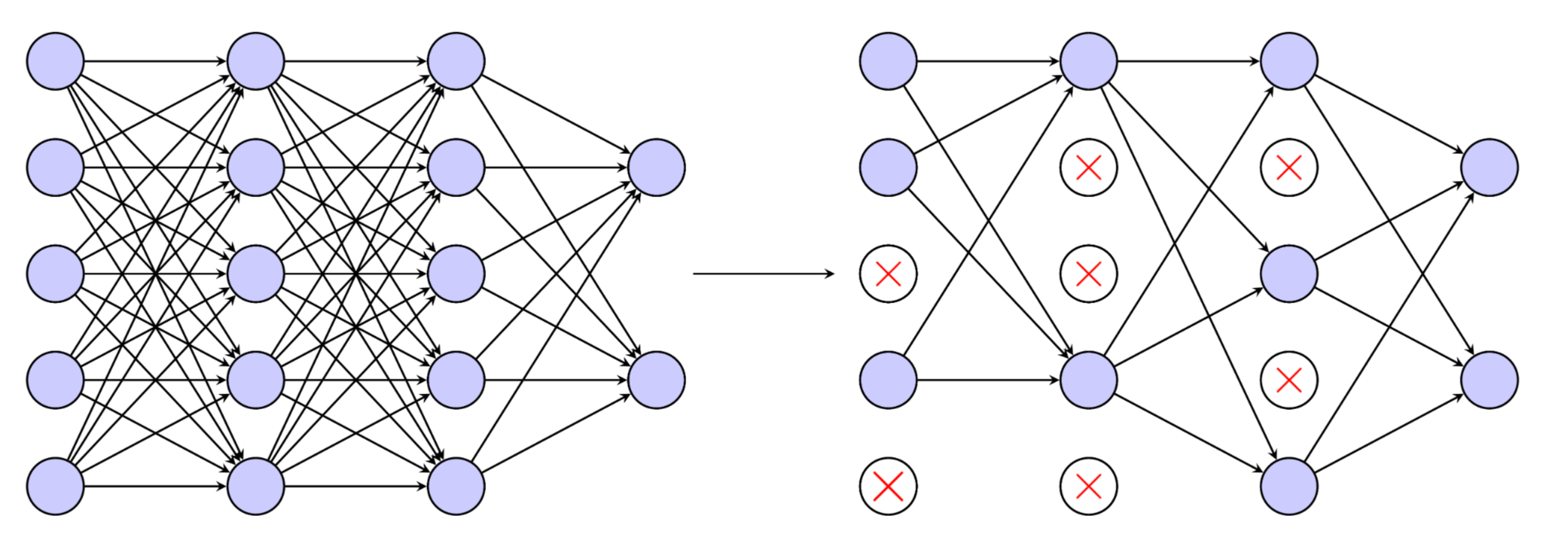
What is Dropout Regularization?

At each training step, randomly remove a fraction of the neurons. Prevents neuron co-adaptation (should be enabled during training time only). It randomly sets a fraction of neuron activations to zero during training, preventing overfitting and improving generalization.

Analogy: Force the bakers to work independently each day, switching who's available, to ensure everyone learns all parts of the baking process.

When is spatial Dropout recommended over typical Dropout?

After convolutional layers it is recommended to rather use spatial dropout, which drops entire feature maps. It drops entire feature maps (channels) rather than individual neurons.

Analogy: Instead of randomly omitting pieces of information, drop them all, creating stronger feature maps.

What parameters should you analyze when putting together an improved network?

Choice of Architecture (layers and nodes), Parameter initialisers, Activation functions, Regularisation, Optimisation algorithm, Learning rate and scheduling. These are hyperparameters and architectural choices that significantly impact model performance.

Analogy: Consider all the levers that go into baking a delicious, mathematically sound cake.