Final Notions & Proofs to Memorize

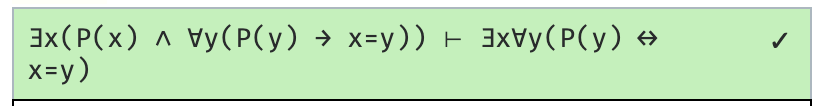
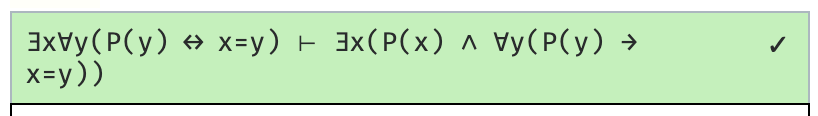
What does this represent: is the deductive system minimally adequate, does it prove only things that it should prove?

soundness

What does this represent: is the deductive system fully adequate, does it prove all the things that it should prove?

completeness

What is FOL soundness?

if P1, .., Pn |- Q then P1, …, Pn |= Q

if we can derive a conclusion from some set of sentences, then the argument must be first-order valid

if |- Q then |= Q

How do we prove soundness? What is the sketch?

with an informal proof

1. any derivation has to be finite (theres a beginning and an end)

2. assume that we have a derivation in which all inferences before the last were made correctly

3. all rules (introduction, elimination, R, X, IP) all yield valid inferences

What is FOL completeness?

if P1, …, Pn |= Q then P1, …, Pn |- Q

if an argument is first-order valid, then we must able to derive the conclusion from some of the sentences that constitutes the premises

if |= Q then |- Q

=I rule

at any point you can write t=t for any name t

no conditions

use when you need a trivial identity statement

often used with =E to swap terms

=E rule

m s=t

n A(…s…s…)

A(…t…t…)

you can replace one, some, all occurrences of a name

works with free variables too

• b = i, L(x,b) derives L(x,i)

AE rule

k AxA(x)

A(t)

you must replace all occurrences of x with t

can be applied multiple times to same universal with different names

AI rule

k A(c)

AxA(x)

conditions:

1. c must NOT appear in any premises, any undischarged assumption (any assumption of an unfinished proof)

2. must replace ALL occurrences of c with x

EI rule

k A(…c…c…)

ExA(…x…c…)

can replace one or more occurrences

x must not already be in formula

EE rule

m ExA(…x…x…)

[ ]A(…c…c…)

[ ]B

B :EEm,i-j

conditions:

1. replace ALL occurrences of x with c

2. c must be fresh (NOT appear in):

   1. any premise

   2. any undischarged assumption (any assumption of an unfinished proof)

   3. the formula ExA(…x…x…)

3. c must NOT appear in B (conclusion that’s exported)