Exponent Properties & Roots (Square & Cube)

Product Law of Exponents

Product Law of Exponents: When multiplying two numbers with the same base, add the exponents together. Example: (a^m) * (a^n) = a^(m+n).

Quotient Law of Exponents

Quotient Law of Exponents: When dividing two powers with the same base, subtract the exponents. (a^{m} \div a^{n} = a^{m-n})›

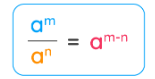
Zero Law of Exponents

Any non-zero number raised to the power of zero is equal to 1.

Negative Law of Exponents

Negative Law of Exponents: When a base is raised to a negative exponent, it is equal to 1 divided by the base raised to the positive exponent.

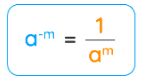
Power of a Power Law of Exponents

(Q) The rule stating that when raising a power to another power, multiply the exponents. (A) (a^m)^n = a^(m*n)

Power of Product Property

Power of Product Property: Exponents of a product can be distributed to each factor. (a*b)^n = a^n * b^n. Simplifies calculations with exponents.

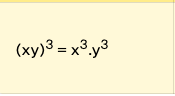
Power of a Quotient Rule of Exponents

Distribute the exponent to both the numerator and the denominator.

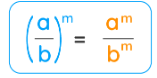
(6a)^2

Example: 
(6a)^2 = 36a^2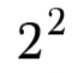

4

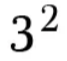
9

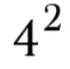
16

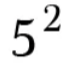
25

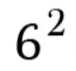
36

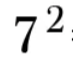
49

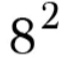
64

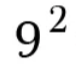
81

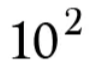
100

Perfect Cubes (raised to the power of 3)

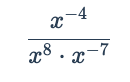
What do we do with NEGATIVE exponents on both parts of the fraction?

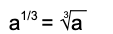
Anything raised to the (1/3) is the same as taking the cube root.

Simplify Square Roots