STAT 164 - Point and Interval Estimation - CHAPTER 4.1

DESCRIPTIVE STATISTICS

gives information that describes the data in some manner

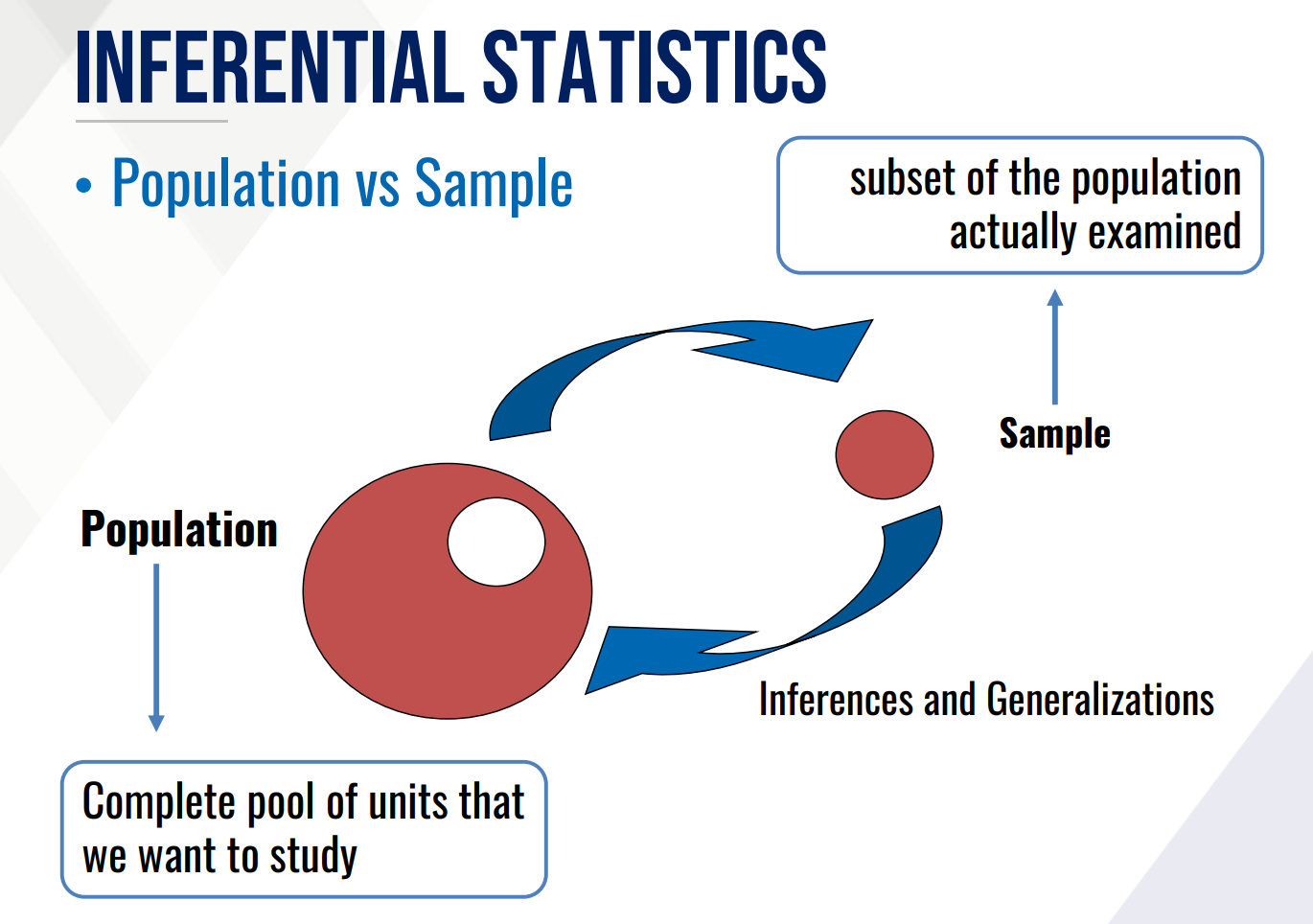
INFERENTIAL STATISTICS

makes a generalization about a larger set where only a part is examined

Parameter

It is a measure observed from a population and is often represented by Greek letters or by capital letters

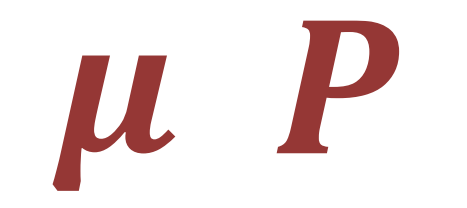
Statistic

It is a measure observed from a sample and is often represented by small letters of by capital letters but with bar or hat on top

ESTIMATION

PROBLEMS ADDRESSED BY INFERENTIAL STATISTICS

concerned with finding a value or range of values for an unknown parameter

TEST OF HYPOTHESIS

PROBLEMS ADDRESSED BY INFERENTIAL STATISTICS

deals with verifying a claim or a conjecture about a parameter or distribution of the population

estimator

An ____________ of a parameter is a rule or formula for computing the statistics using the sample data.

It gives a numerical value called an estimate.

Accuracy

PROPERTIES OF AN ESTIMATOR

measures the closeness of an estimate to the true value

Accuracy

PROPERTIES OF AN ESTIMATOR

It is measured by the bias which is the difference between the expected value of the estimate and the parameter.

Precision

PROPERTIES OF AN ESTIMATOR

measures the closeness of the different possible values of the estimator to each other.

Precision

PROPERTIES OF AN ESTIMATOR

It is measured by the variance or its standard error.

Point Estimator

an estimator that gives a single value in estimating a parameter

Interval Estimator

an estimator that gives a range of values for estimating a parameter

RELATED SAMPLES

each observation in the first set of samples is matched or paired with an observation in the second set of samples (matched/paired vs self paired)

INDEPENDENT SAMPLES

samples are drawn independently from the two populations to be compared

• no hint of pairing or matching

Which type of sample?

Comparing the mean length of stay in the hospital of Hepatitis B patients with cirrhosis and without cirrhosis

Which type of sample?

Verifying if the mean height of 20 boys and 17 girls at age 9 are the same.

Which type of sample?

Testing the clearance rate of a drug by measuring its blood concentration among treated patients two hours and 10 hours after intake.

Which type of sample?

Comparing the temperature of male and female cats, paired by age and breed, after receiving a vaccine

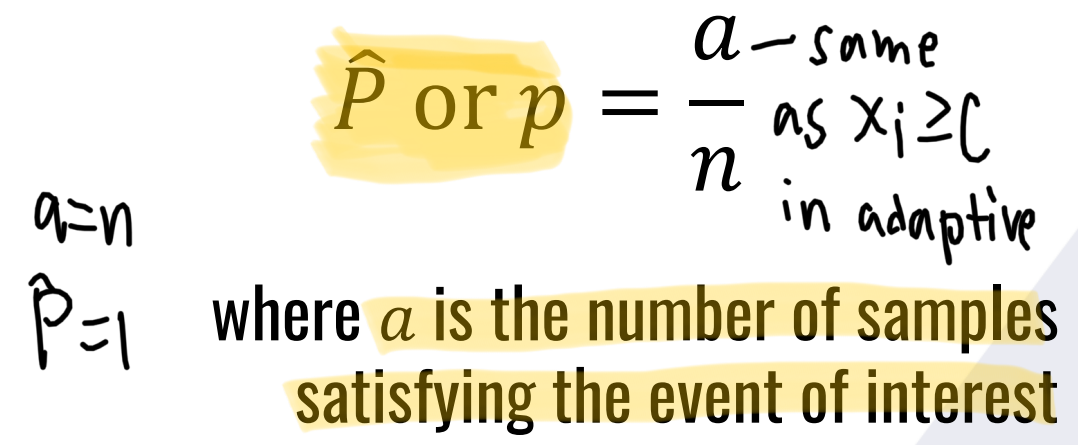
What is the Point Estimator formula for the paramete:

Proportion, P

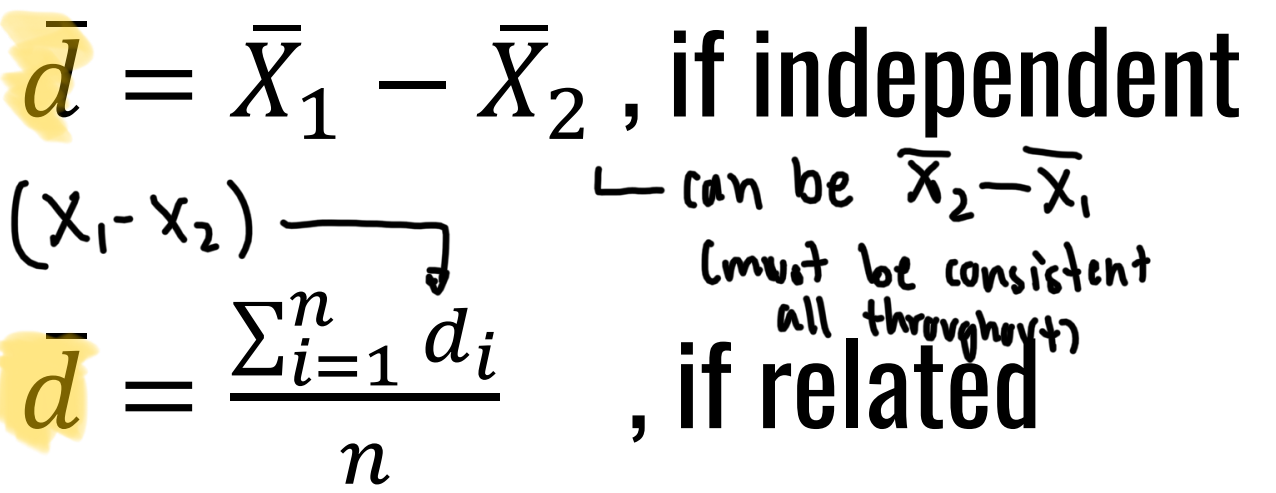
What is the Point Estimator formula for the paramete:

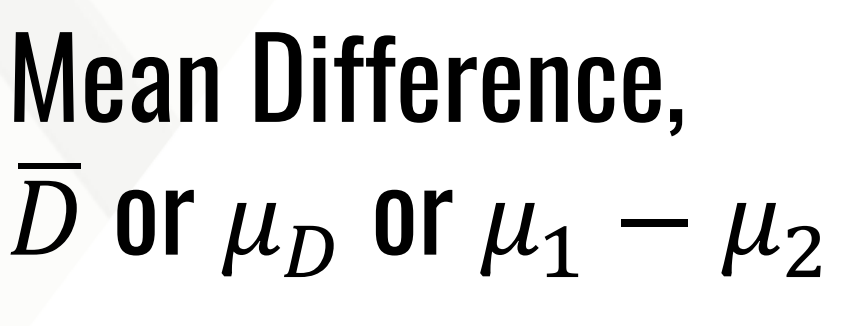
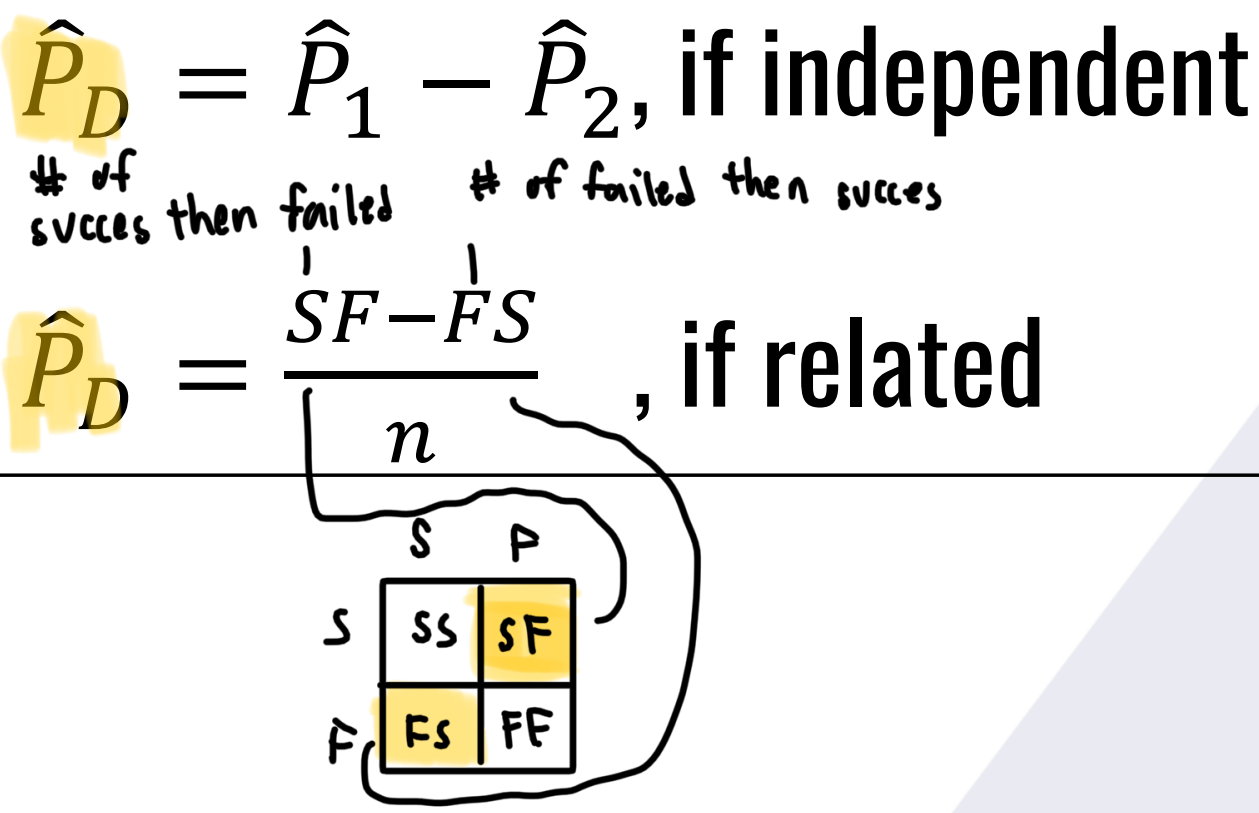
What is the Point Estimator formula for the paramete:

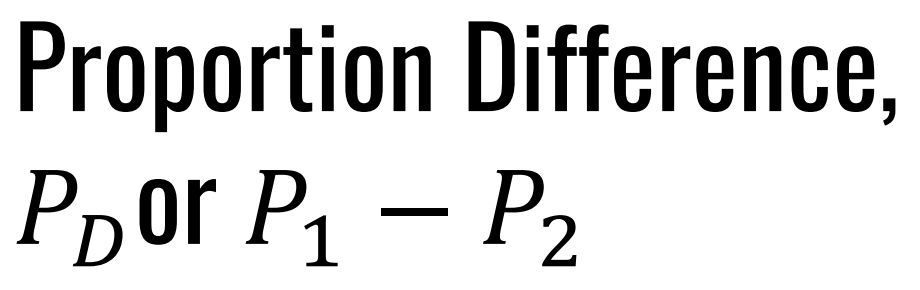
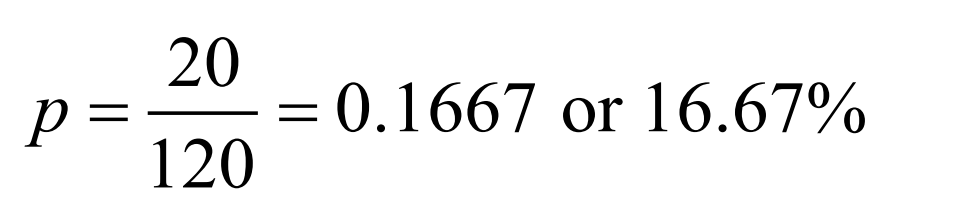
Find the proportion.

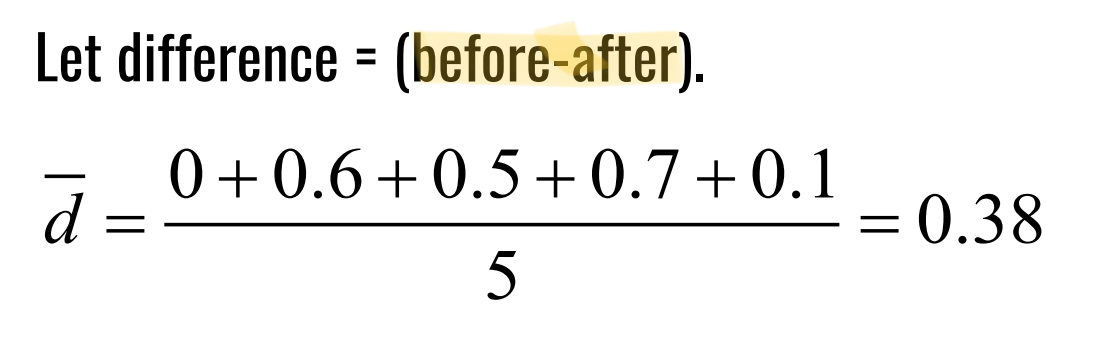
Find the average difference

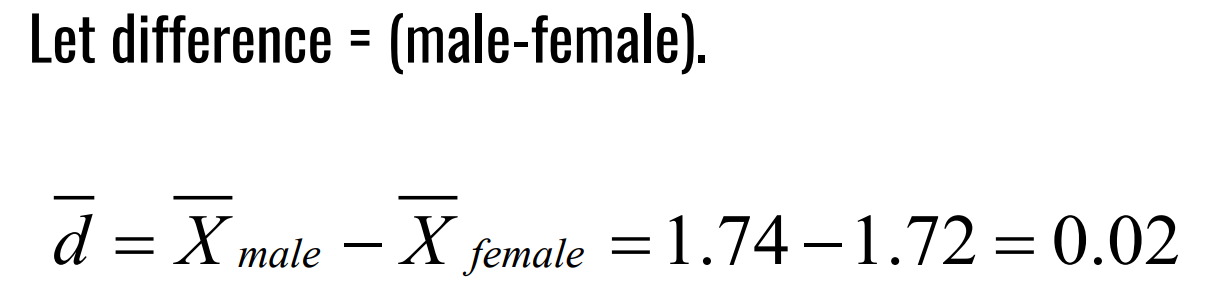
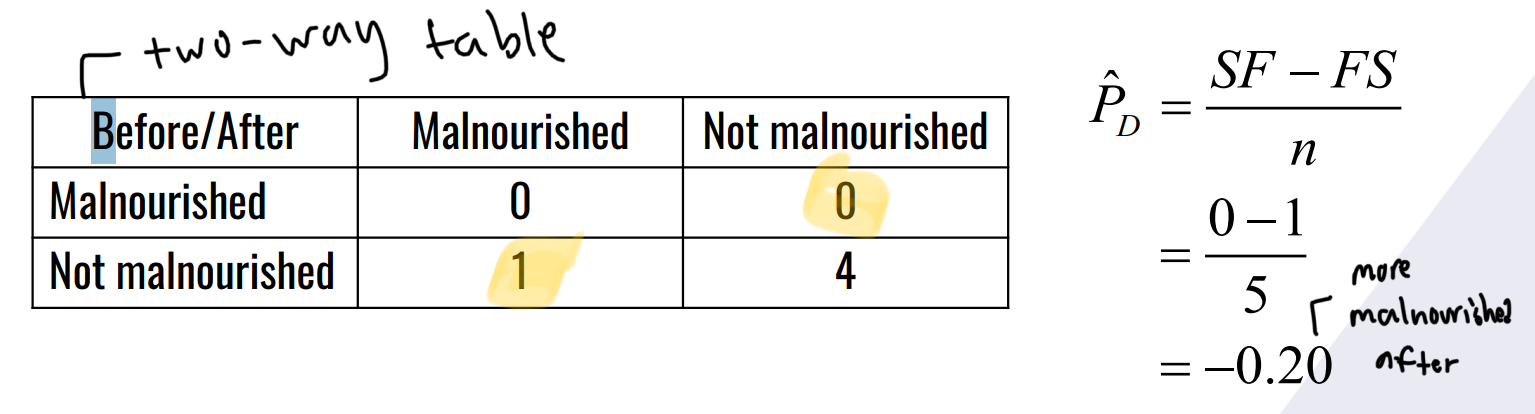
malnourished male migratory birds (weight < 1kg)

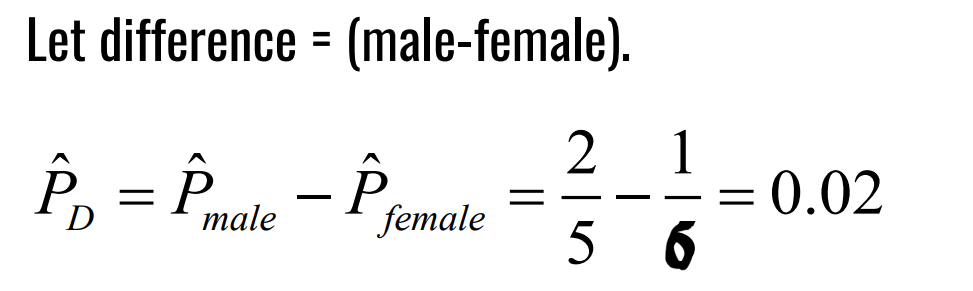
confidence coefficient

An interval estimate becomes a confidence interval estimate of a parameter if a _______________ is attached to it.

1-α

A confidence coefficient, ______, is the level of confidence we attach to an interval to indicate how confident we are that the parameter is within the interval

• The level of confidence may range from 0% (no confidence) to 100% (with certainty).

GENERAL STEPS IN CONSTRUCTING CI:

1. Specify the desired level of confidence by determining the value of α.

2. Find the tabular value which corresponds to α.

3. Compute for point estimate.

4. Compute for the standard error of the point estimate.

5. Compute for the upper and lower limits of the interval.

GENERAL STEPS IN CONSTRUCTING CI:

1. Specify the desired ________ by determining the value of ________.

2. Find the ________ which corresponds to ________.

3. Compute for ________.

4. Compute for the ________ of the ________.

5. Compute for the ________ of the interval.

STANDARD ERROR (se)

It is the standard deviation of the point estimate

STANDARD ERROR (se)

It measures the precision of the point estimate

[point estimate ± (tabular value x se)]

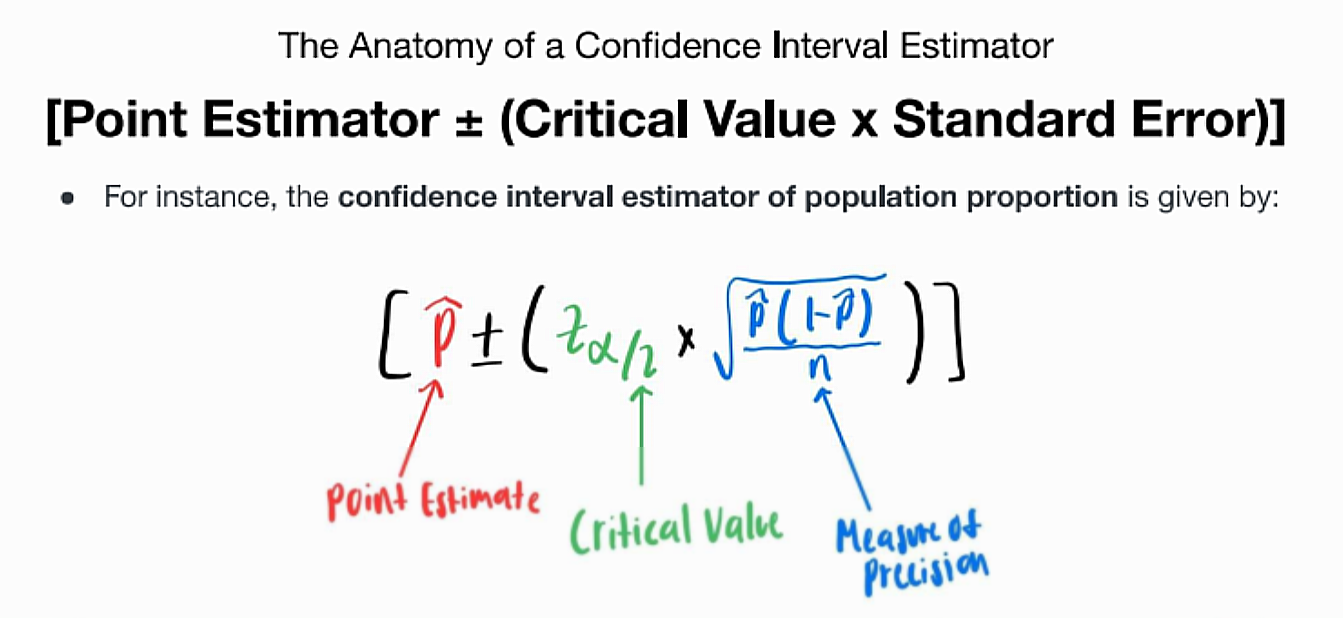
What is the General form of CI Estimate for Symmetric Distributions?

Population Mean, if σ is known

CONFIDENCE INTERVAL ESTIMATOR formula for?

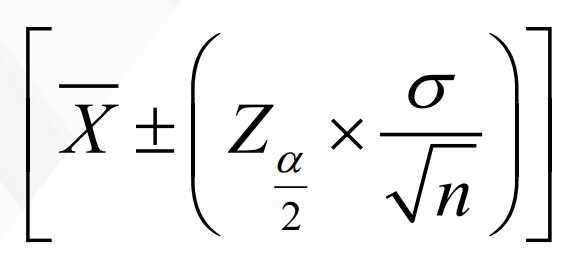
Population Mean, if σ is unknown

CONFIDENCE INTERVAL ESTIMATOR formula for?

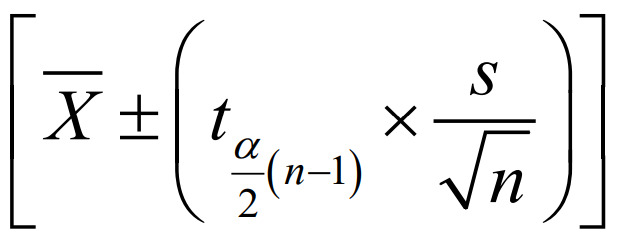
Population Mean, if σ is unknown but n ≥ 25

CONFIDENCE INTERVAL ESTIMATOR formula for?

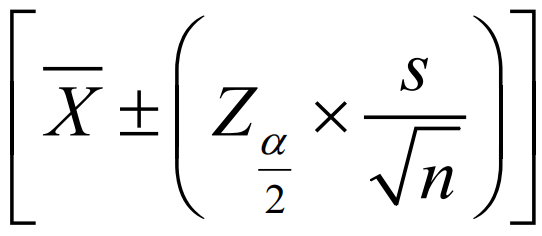
Population Proportion

CONFIDENCE INTERVAL ESTIMATOR formula for?

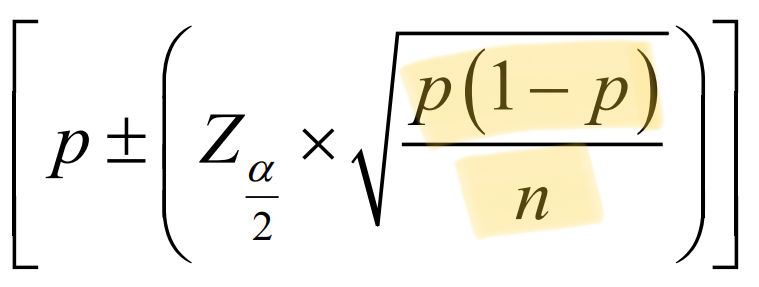
Population Mean Difference (Independent), If variances are known

CONFIDENCE INTERVAL ESTIMATOR formula for?

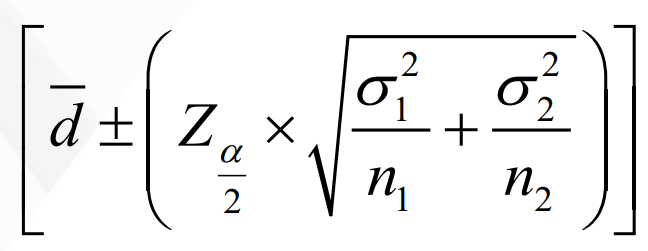
Population Mean Difference (Independent), If variances are unknown assumed equal

CONFIDENCE INTERVAL ESTIMATOR formula for?

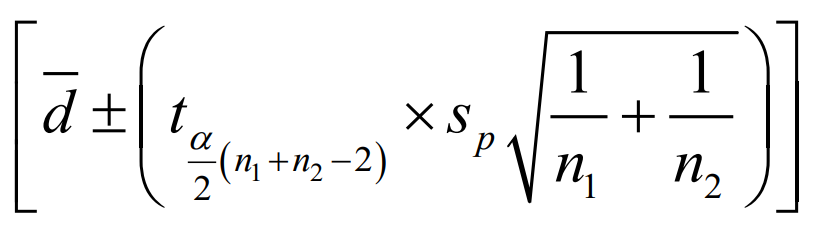
Population Mean Difference (Independent), If variances are unknown assumed unequal

CONFIDENCE INTERVAL ESTIMATOR formula for?

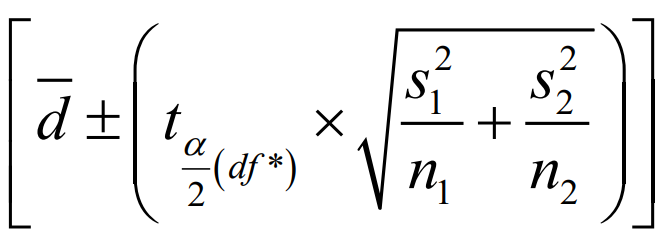
Population Mean Difference (Related), if σ_d is known

CONFIDENCE INTERVAL ESTIMATOR formula for?

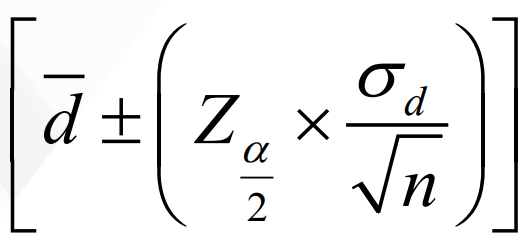
Population Mean Difference (Related), if σ_d is unknown

CONFIDENCE INTERVAL ESTIMATOR formula for?

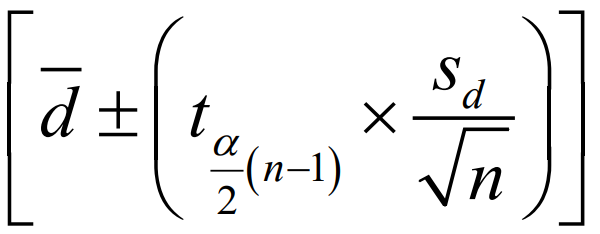
Population Mean Difference (Related), if σ_d is unknown but n ≥ 25

CONFIDENCE INTERVAL ESTIMATOR formula for?

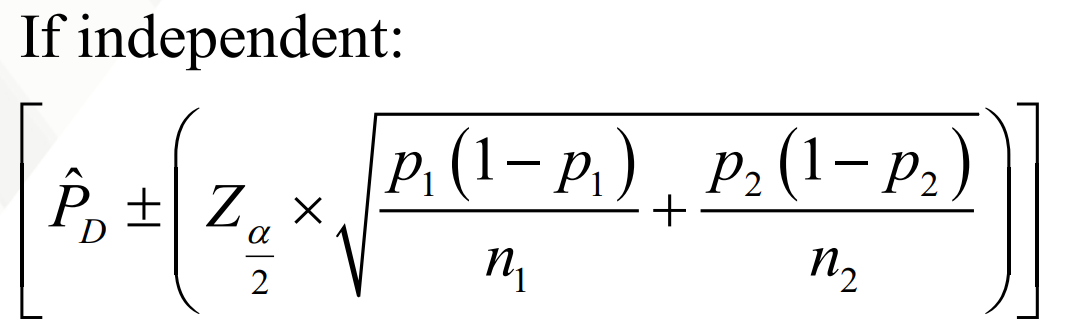
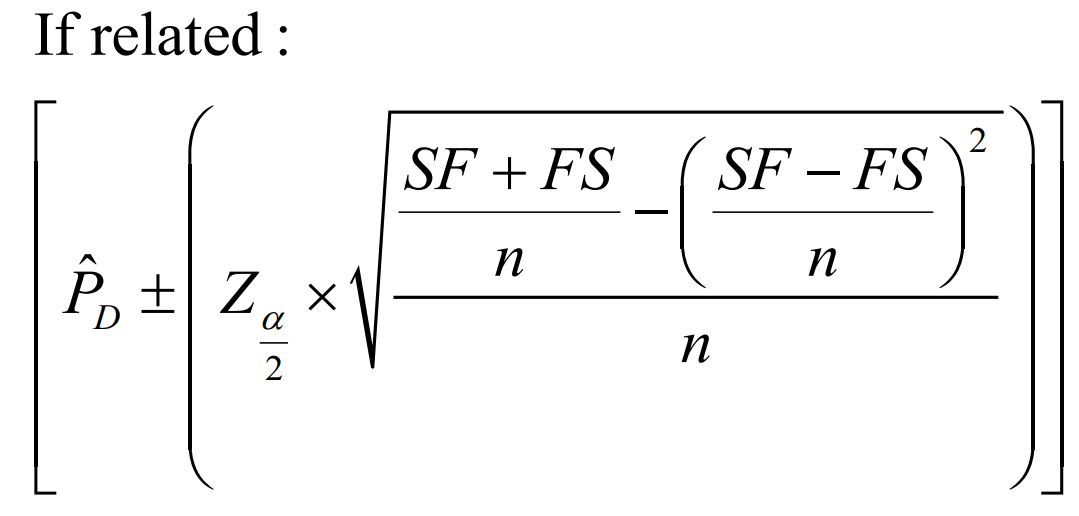
CONFIDENCE INTERVAL ESTIMATORS

Population Difference of Proportion 

If independent, formula?

CONFIDENCE INTERVAL ESTIMATORS

Population Difference of Proportion 

If related, formula?

Z_0.01 = 2.33

t_0.005(9) = 3.25

t_0.05(9) = 2.262

(1-α)%; true

SOME PROPERTIES OF CI Estimates:

If sampling of the same sample size is done multiple number of times, _______ of CI’s constructed will include the ______ value of the parameter.

precision; less; more

SOME PROPERTIES OF CI Estimates:

The length (UL – LL) of the CI estimate is a measure of its _________. Wider CI is ______ precise while narrower CI is ______ precise.

Increasing; increases

SOME PROPERTIES OF CI Estimates:

__________ the sample size __________ the precision of the CI estimate.

Increasing; decreases

SOME PROPERTIES OF CI Estimates:

__________ the confidence level __________ the precision of the CI estimate.