RCA theorems

algebra of open sets

union of arbitrarily many open sets is open

intersection of finitely many open sets is an open set

algebra of closed sets

union of finitely many closed sets is closed

intersection of arbitrarily many closed sets is closed

theorem 5.8

composition of continuous functions are continuous

Intermediate value theorem

f: [a,b] → R is CONT and f(a) ≠ f(b)

and λ lies between f(a) and f(b) then ∃ c in (a,b) s.t

f(c ) = λ

fixed point theorem

if f: [a ,b] → [a,b] is cont then ∃ c in [a,b] s.t

f(c ) = c

use the gx = ? - f(x) then show this equal 0 using IVT

make sure explain how g is cont on [a,b] etc

Boundedness theorem 8.3

A cont function on close bounded interval is bounded and attains its bounds

cont on [a,b] so achieves sup and inf

theorem 9.1

f: [a,b] → is cont then

f([a,b]) = [m,M]

both inf and sup are attained on [a,b]

Inverse function theorem 9.5

f: [a,b] → [c,d] is cont and strictly increasing

f(a) = c and f(b) = d

inverse f^-1 exists = continuous, strictly increasing and surjective

uniform convergence def

for each ε >0 ∃ N in Natural depending on ε NOT on x s.t

|fn(x) - f(x)| < ε when n >= N

criterion for non uniform convergence

for some ε >0 there exists a subsequence fnk of fn and a sequence of points xk st

|fnk(xk) - f(xk) | >= ε for all k in N

f is the pointwise function

theorem 10.3 cont uniform

if fn converges uniformly to f then f is a continuous function

theorem 14.1 abt diff dy/dx

f satisfies inverse function theorem and y = f(x). f is differentiable at x and f’(x) ≠ 0 then

(f^-1)’ (y) = 1/ f’(x')

15.7 rolles theorem

f is cont on [a,b] and diff on (a,b) and f(a) = f(b)

there exists c in (a,b) s.t f’(c ) = 0

16.1 mean value theorem

f is cont on [a,b] and diff on (a,b) then there is c in (a,b) s.t

f(b) - f(a)

— ——— = f’(c )

b - a

generalised mvt use for taylors

f &g are cont on [a,b]

diff on (a,b) and g’( c) ≠ 0

f(b) - f(a). f ‘ (c )

—- ——— = ———-

g(b) - g(a) g ‘ (c )

set is open if

every point of S is an interior point of S

boundary point

some on the inside some on the out

harmonic function

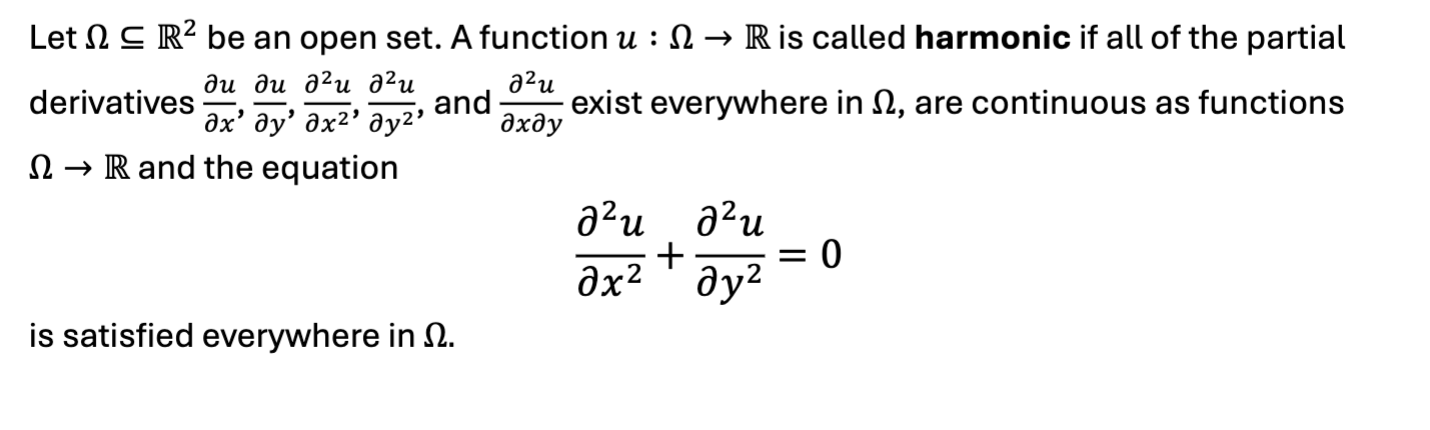
cauchy gorsat theorem

simple closed contour and f is holomorphic then the integral = 0

cauchys residue theorem

Let Ω ⊆ ℂ be a simply connected, open set, 𝐾 ∈ ℕ and 𝑧1, 𝑧

,2, … , 𝑧𝐾 ∈ Ω, 𝑓: Ω ∖

{z1, 𝑧2, … , 𝑧𝐾} → ℂ be a holomorphic function and Γ ⊆ Ω ∖ {z1, 𝑧2, … , 𝑧𝐾} be a simple,

closed contour with the standard orientation.