linear independence, basis, subspace

vectors v1, v2, …, vr are linearly independent iff

the only way that c1v1 + ... + crvr = 0 is if all the ci are zero

in Rⁿ, no set can have more than

n linearly independent vectors; if m > n, then any set of m vectors in Rⁿ must be linearly dependent

c1v1 + … + cnvn = 0 is trivial if

c1 = c2 = … = cn = 0

1 vector is linearly independent iff

it is not the zero vector

2 vectors are linearly independent iff

they are not on the same line

3 vectors are linearly independent iff

they are not on the same plane

span of 1 linearly independent vector is

a line

span of 2 linearly independent vectors is

a plane

span of 3 linearly independent vectors is

a 3d space

smallest span of vectors is

zero

the vectors v1, v2, …, vk are said to be a basis of the set v (with v being the span of some vectors u1, u2, .. uj) if

they are linearly independent and span v such that the spans of v and u are equal

parametric equation of a plane

p = p₀ + tu + sv , where p₀ is a point in the plane and u, v are two noncollinear vectors on the plane

subspace of Rⁿ

a set of vectors in Rⁿ that can be described as a span

given n vectors in Rⁿ, how can you tell whether the set of them is a basis of Rⁿ

check linear independence; need n leading ones in rref of [ v1 v2 … vn | 0 ], with one in each row

if {x1, x2, …, xm} and {y1, y2, …, yk} are basis of a subspace of Rⁿ, then

m = k

a set V of vectors in Rⁿ is a subspace if (definition)

the set includes the zero vector and it is closed under addition and scalar multiplication

vectors are a basis of a subspace V if

they span V and are linearly independent

a basis of a subspace V is the

minimal set of vectors needed to span all of V

dimension of a subspace V is

number of vectors in its basis

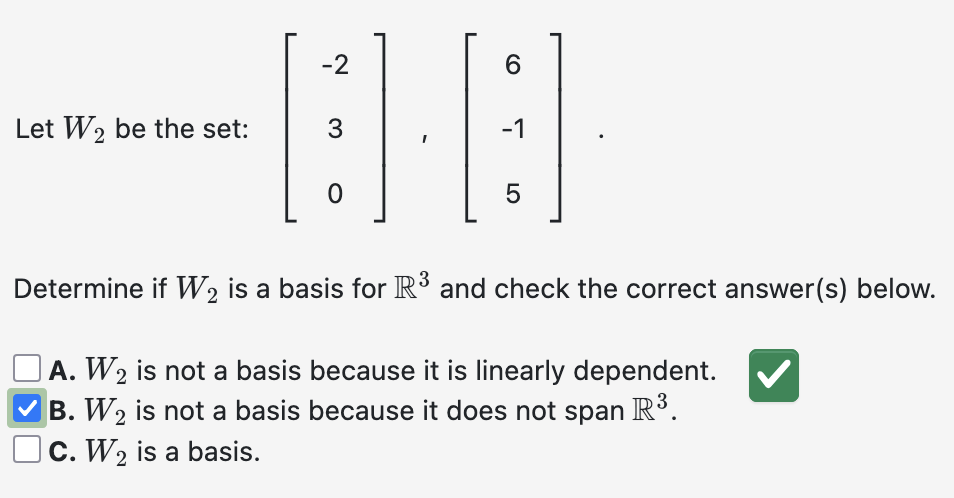
why does it not span R³

there are only two vectors - 3 linearly independent vectors are needed to span R3