WJEC AS Maths Unit 1 (Pure)

Laws of indices

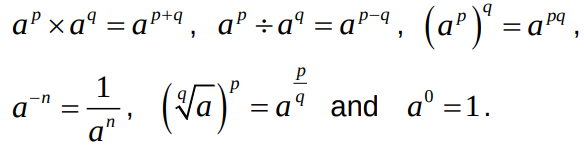
Rules for manipulating surds

Rationalising the denominator

multiply the fraction by the denominator (bottom) with a changed. multiply out using surd rules

discriminant rule for 2 real and distinct roots

b² - 4ac > 0

discriminant rule for 2 equal real roots/1 repeated real root

b² - 4ac = 0

discriminant rule for no real roots

b² - 4ac < 0

methods for finding the nature of roots of a quadratic and the critical values/values which satisfy the inequality made

1. use discriminant rule for the conditions provided, e.g. no real roots

2. substitute the values of a, b, and c into the discriminant to form an equation

3. factorise this equation

4. to find critical values, draw onto a graph. where the y-values are positive, these are your critical values, e.g. if it’s a positive quadratic with -2 and 2, k< or equal to -2 and k > or equal to 2

completing the square

• used to find maxima and minima or solve quadratic equations

• minima are found from positive quadratics (a>0). maxima are found from negative quadratics (a<0)

• method;

  1. half the coefficient of x and place after the x in the bracket

  2. subtract this squared

  3. add/subtract c

• ax² + bx + c = 0 —> (x+a)² + b

• find maxima or minima; least or greatest value is the one subtracted from y (outside the bracket). when x= the value inside the bracket, with changed sign. maxima or minima= (when x= value, least or greatest value)

• 1/ least=greatest and 1/greatest=least

methods for solving quadratics

1. factorisation

2. quadratic formula

3. completing the square

quadratic formula

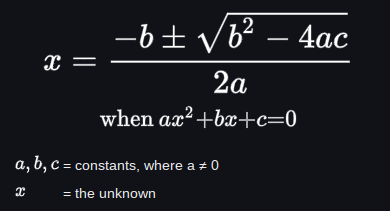
factorising quadratics

• use product of ac (a multiplied by c) and sum of b

simultaneous equations

• used for finding points of intersection/contact between two lines, a line and a curve or two curves

• elimination = either point of intersection of two lines of a quadratic curve and a line

• substitution = used for all situations

1. Elimination; (multiply the equations by suitable numbers to make one variable have the same coefficient. add or subtract the equations (same sign = subtract, different sign = add)

2. Substitution; make x or y the subject of one of the equations and substitute into the other. factorise new equation to find x and substitute into orgininal equation to find y

solving inequalities

1. linear inequalities; solve as a regular equation. when multiplying by a negative number, change all signs including the inequality sign

2. quadratic inequality; factorise, find critical values, sketch. below the x-axis=1 region=1 inequality. above the x-axis=2 regions=2 inequalities.

factor theorem

• if f(a)=0 then (x-a) is a factor of f(x)

• if (c/a)=0 then (ax-c) is a factor of f(x)

• Methods; 1. algebraic division. 2. comparing coefficients

• algebraic division; determine what you need to multiply the factor by to find the terms in the quadratic. should divdide to 0 for it to be a factor. remainder is the solution

• comparing coefficients; find the coefficients by determining what each of the tersm in the quadratic need to be multipled by, using the factor

Proof notation

Laws for all integers on n

Proof by deduction

• Start from known facts or definitions, then use logical steps to reach desired conclusion

• Can be proof of log laws and differentiation from first principles

• Series of logical steps

Proof by exhaustion

• proves a statement is true by checking every possible case separately

Proof by counter-example

• used to prove something is false

• Need to find 1 example for which a statement does not hold true in order to show that the statement is not always true

sketching quadratic curves

• positive x² u-shaped curve

• negative x² n-shaped curve

sketching cubic curves

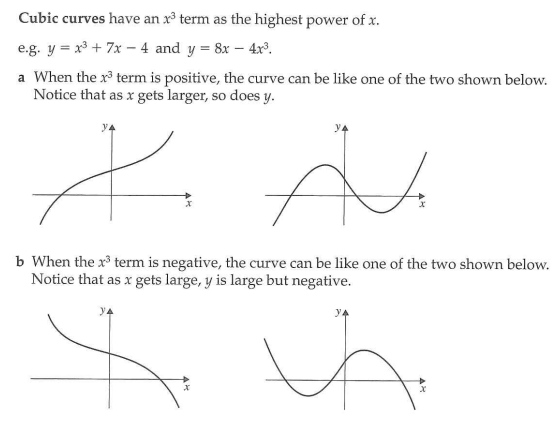
sketching reciprocal curves

y=af(x)

a=number of times peak is moved up or down in y

y=f(x)+a

a=number of times minimum is moved up/down

+a=up a times

-a=down a times

y=f(x+a)

a=number of times graph is moved horizontally

+a=moved left

-a=moved right

y=f(ax)

a=how much graph is tretched horizontally

y=f(2x)= halfed

y=f(1/2x)= doubled

y=-f(x)

graph is flipped in y-axis

y=f(-x)

graph is flipped in x-axis

equations of a straightline

y=mx+c

y-y₁ = m(x-x₁ )

ax+by+c=0

things needed for equation of a straight line

• a point on the line

• gradient

• y-y₁ = m(x-x₁ )

the equation of a straight line of gradient, m, passing through (x,y)

y-y₁ = m(x-x₁ )

gradient of a line jpining two given points

gradient, m = y₂ - y₁ / x₂ - x₁

finding the lenght of a line jpining tqo given points

√(x₂ - x₁ )² + (y₂ - y₁ )²

midpoint of a line joining two given points

M = (x₁ + x₂ / 2, y₁ + y₂ / 2)