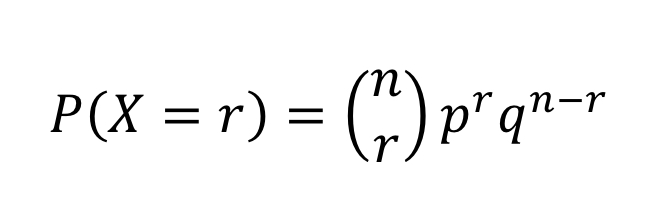unit 3 methods terminology (ch 8, 9, 10 & 11.2)

just any formulas, terms etc that i should memorise...

to find the x intercepts…

let f(x) = 0

to find the POI…

let f’’(x) = 0, and sub in a value above and below the result to check the change in sign (if one value is above 0, and if one is below 0)

how do you find the SP’s of a function?

let f’(x) = 0

how do you determine the nature of SP’s?

substitute each SP value into f’’(x) to determine it’s concavity, and then substitute the SP values into f(x) to find the y coordinates

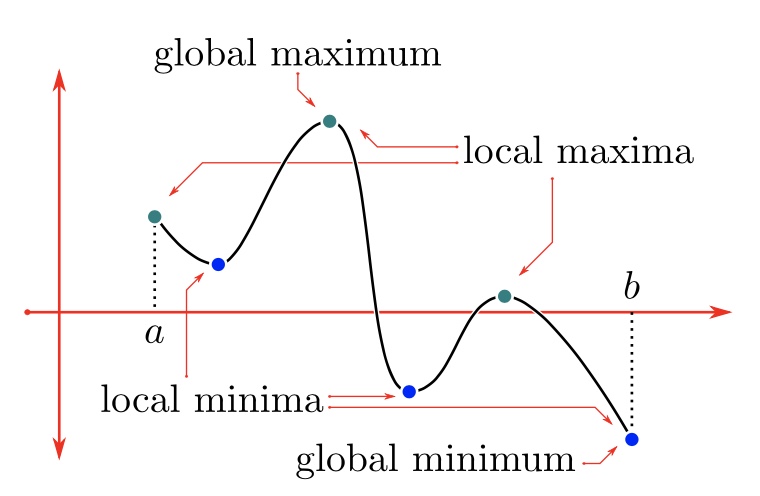
what are the steps to finding the key features of a function on a graph???

1. differentiate and double differentiate the function. this will make it much easier to work out everything else

2. find the x intercepts

3. find the SP’s and their natures

4. find the POI’s

what is the local maxima??

the greatest value on the interval of a function

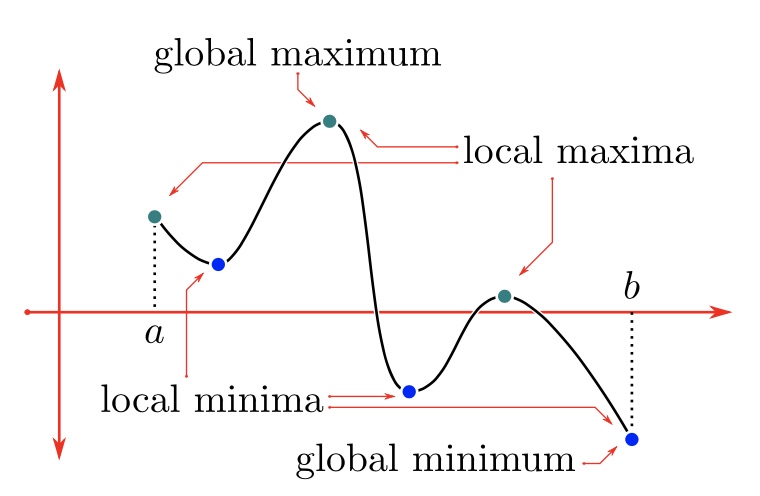
what is the local minima?

the least value on the interval of a function

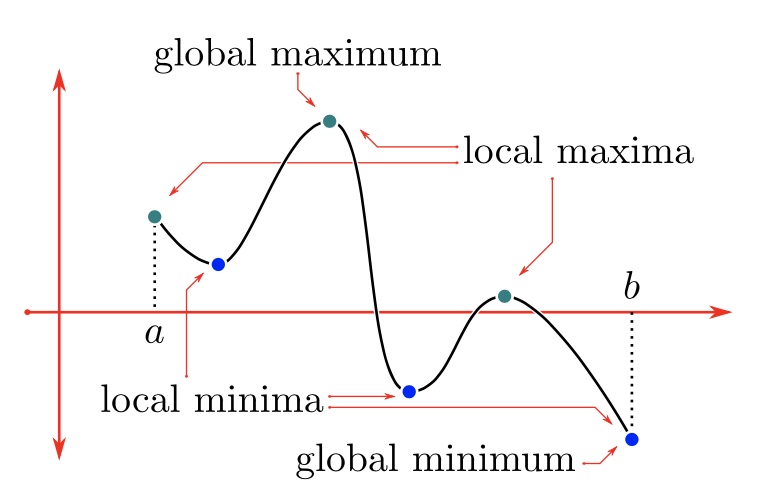
what is the global maxima?

the greatest value for the entire function

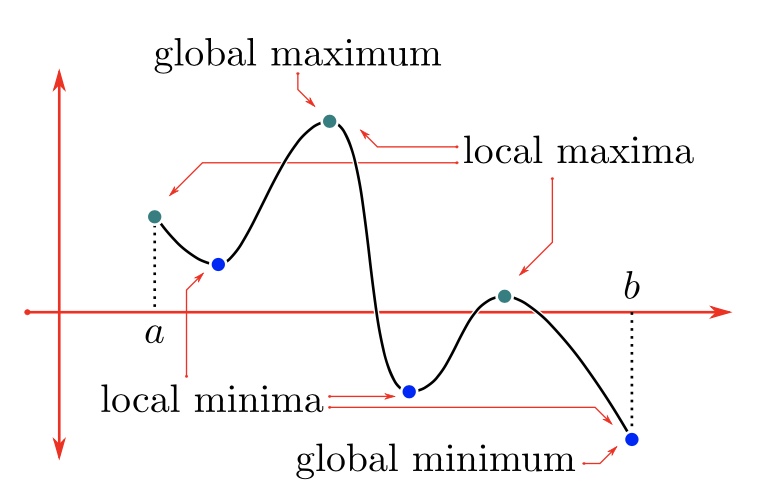
what is the global minima?

the least value for the entire function

minima will occur when:

f’(x) = 0

and

f”(x) > 0

maxima will occur when:

f’(x) = 0

and

f”(x) < 0

steps for determining the location and nature of maxima and minima:

1. differentiate f(x)

2. solve for x when f’(x) = 0 to determine the x coordinate of the stationary point

3. determine the value of f”(x) at the stationary point

• if f”(x) > 0, the stationary point is a maximum

• if f”(x) < 0, the stationary point is a minimum

4. sub the x coordinate of the SP into the original function, f(x) to determine the y coordinate

steps for optimisation problems:

1. Draw a diagram and label it with as few variables as possible.

2. Determine a connection between the variables from the information given.

3. Determine an expression for the quantity to be maximised or minimised in terms of the one variable.

4. Differentiate the expression to determine stationary point(s).

5. Check the nature of the SP’s by either substituting into f’’(x) or using a sign diagram.

6. Check whether the answer is the absolute maximum or minimum by evaluating the end points of the domain.

7. Sketch the graph the function to check for realistic values.

8. Answer the actual question.

the sine rule

“in any triangle, ABC, the ratio of each side to the sine of its opposite angle will be equal”

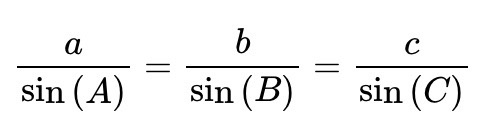
what information do we need to be able to use the sine rule?

We can use it when we're given the sizes of:

1. two sides and one angle (which is opposite to one of these sides)

2. one side and any two angles.

the cos rule

what information do we need to be able to use the cos rule?

Use this formula when given:

• the sizes of two sides and its included angle

• three sides of the triangle

if y = f(x):

• the first derivative, f’(x), is the rate of change of y with respect to x, or in other words, the gradient of the curve

• the rate of change of the derivative with respect to x is the second derivative.

a function is concave up when:

the gradient of the function is increasing, so the rate of change of the gradient is positive

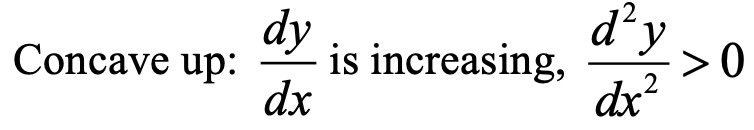
a function is concave down when:

the gradient of the function is decreasing, so the rate of change of the gradient is negative

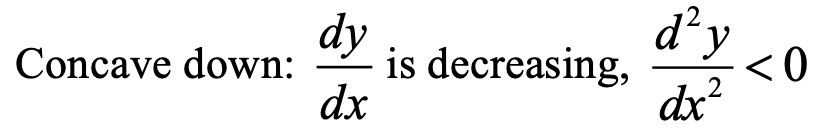
On a continuous curve, the point where the concavity changes is called:

a POI (point of inflection)

For a point of inflection, the following must be true:

f’’(x) = 0 AND the sign concave up: changes either side to show the change in concavity

A stationary point on a curve is defined as:

·       a point where the gradient (f(x)) is 0

At a maximum turning point…

the curve is concave DOWN

At a minimum turning point…

the curve is concave UP

Velocity is:

the rate of change of displacement with respect to time, dx/dt.

Acceleration is:

the second derivative of displacement with to time, d²x/dt²

sin (θ) = …

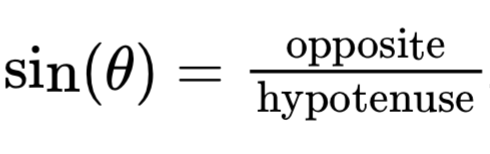
cos (θ) = …

adjacent/hypotenuse

tan (θ) = …

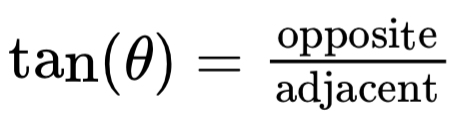
domain and range of sine and cosine:

domain: R

range: [-1, 1]

domain and range of tangent:

domain: R \ {± π/2, ± 3π/2, …}

and…

range: R

the ambiguous case of the sine rule…

When we are given…

• two side lengths of a triangle

• an acute angle opposite one of these sides,

there are two different triangles we can draw.

For the ambiguous case of the sine rule to be applicable, the following conditions must be met:

• The given angle must be acute.

• The adjacent side must be bigger than the opposite side.

• The opposite side must be bigger than the adjacent side multiplied by the sine of the given angle.

To calculate angle sizes, the cosine rule can be written as:

cos (A) = b² + c² - a² / 2bc

cos (B) = a² + c² - b² / 2ac

cos (C) = a² + b² - c² / 2ab

area of a right angled triangle:

A = ½ base x height

area of a triangle that is NOT right angled:

(where C is the angle included between sides a and b)

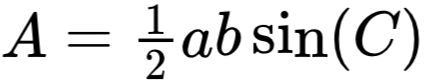
how can you quickly determine the largest angle in a triangle?

find the longest side, and the angle opposite it will be the largest angle.

how can you quickly determine the smallest angle in a triangle?

find the shortest side, and the angle opposite it will be the smallest angle.

area of a triangle (cosine and sine rules)

area △ = ½ ab sin (C)

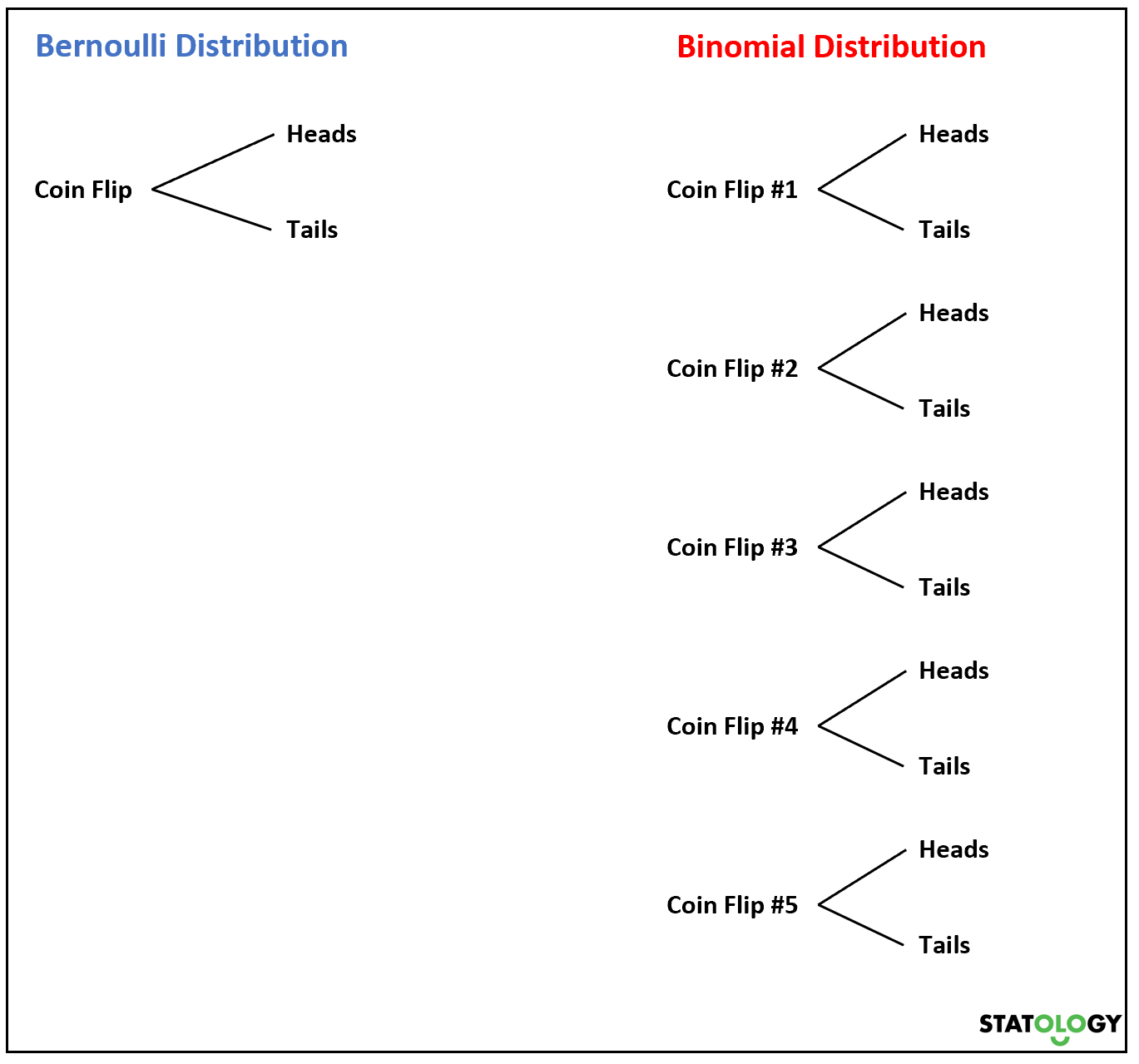
what is a Bernoulli distribution?

a discrete probability distribution of the simplest kind

Bernoulli distributions are controlled by the probability of success, p. The probablility of failure, q, is equal to 1 - p.

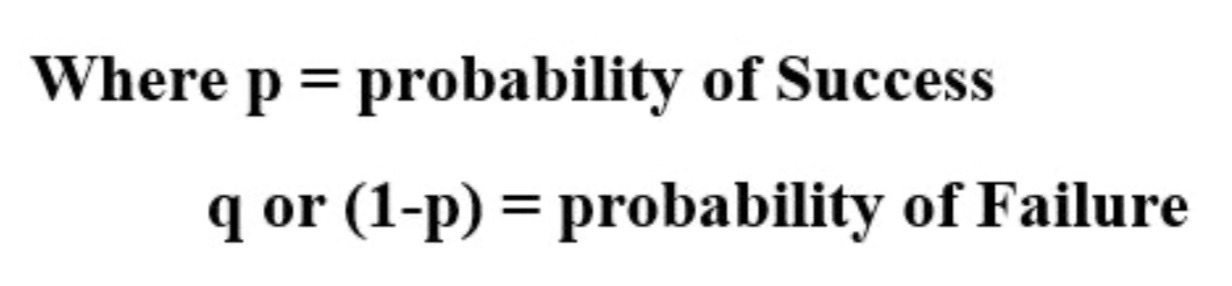
what does the term, “Bernoulli trial”, refer to?

a single event that has only 2 possible outcomes, success of failure, with each outcome having a fixed probability

what is a Binomial distribution?

it results when a Bernoulli trial is carried out a number of times.

they involve one trial with only two possible outcomes, and the probability of success is known (stated in the question)?

the characteristics of a binomial distribution:

1.     The trials must be independent, meaning the Pr of one event isn’t affected by the outcomes of other events, and stays the same for each trial.

2.     Only two possible outcomes must exist for each trial — success and failure.

the variance of a Bernoulli distribution:

p(1-p)

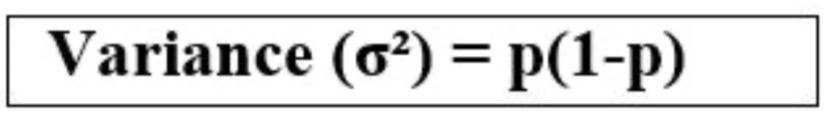
the standard deviation of a Bernoulli distribution:

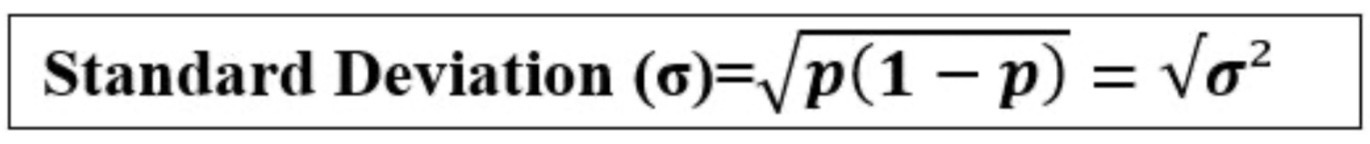
For a binomial distribution, the probability of getting r successes out of n trials can be calculated using the equation:

where:

• n= the number of trials (or the number being sampled)

• x= the number of successes desired

• p= probability of getting a success in one trial

• q = 1 - p = the probability of getting a failure in one trial

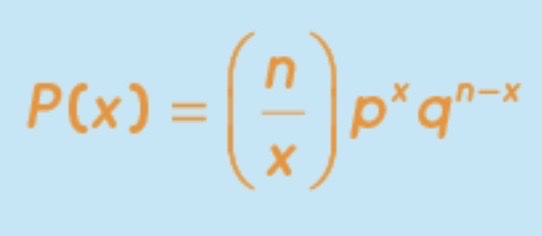
the notation for some event X—that is a Binomial distribution—is represented by:

X ~ Bi(n, p)

what is BinomPdf used for???

its used to calculate probabilities for a single r value,

i.e. For X ~ Bi(10, 0.6), Pr (X = 5) = BinomPdf(10, 0.6, 5) = 0.2007 = 20.07%

what is BinomCdf used for?

its used to sum the probabilities for r values on an interval.

i.e. For X ~ Bi(10, 0.6):

• Pr(2 ≤ X ≤ 7) = BinomCdf (10, 0.6, 2, 7) = 0.2007 = 20.07%

• Pr(X ≤ 6) = BinomCdf (10, 0.6, 0, 6) = 0.6177 = 61.77%

• Pr(X > 8) = Pr(X ≥ 9) = BinomCdf (10, 0.6, 9, 10) = 0.0464 = 4.64%

what is InvBinom used for?

it’s used to calculate the number of trails needed such that P(X≤ r) ≤ c

Eg. For X ~ Bi(10, 0.6), the no. of trials needed to hahve a less than 30% chance of having 4 successes or less is equal to:

n = InvBinomN (0.3, 0.6, 4) = 9

Nine trials are needed so that the probability of getting 4 or less successes is lower than 30%

pascall’s triangle

the mean of a bernoulli distribution

= p

the difference between a bernoulli and binomial distribution is…

what is a continuous random variable (CRV)?

a random variable that assumes quantities that can be measured, such as weights, time, height, in a given range

i.e. height, weight, the amount of sugar in an orange, the time required to run a mile

what is relative frequency?

it refers to actual data obtained

relative frequency formula

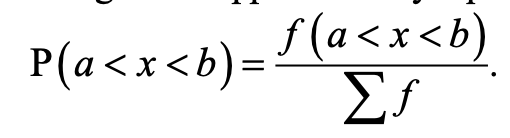
what is a probability density function (or pdf)?

it is a function that represents probabilities of a given scenario for the interval x E [a, b].

what conditions must be met for a function to be classified as pdf?

Two conditions must be met for a function to be classified as this:

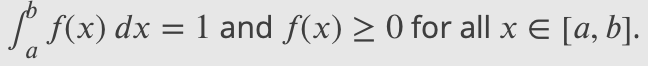
The probability of a variable lying within a particular interval is…

also equal to the fraction of the histogram area that the column for that interval occupies

The probability that a continuous random variable X lies between the values a and b is given by:

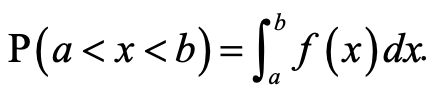
The probability of x having an exact value is:

0

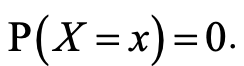
d/dx(x(t)) = …

v(t)

d/dx(v(t)) = …

a(t)

the formula for calculating the probability of seeing r successful outcomes out of n trials where the probability of success for one trial is p: