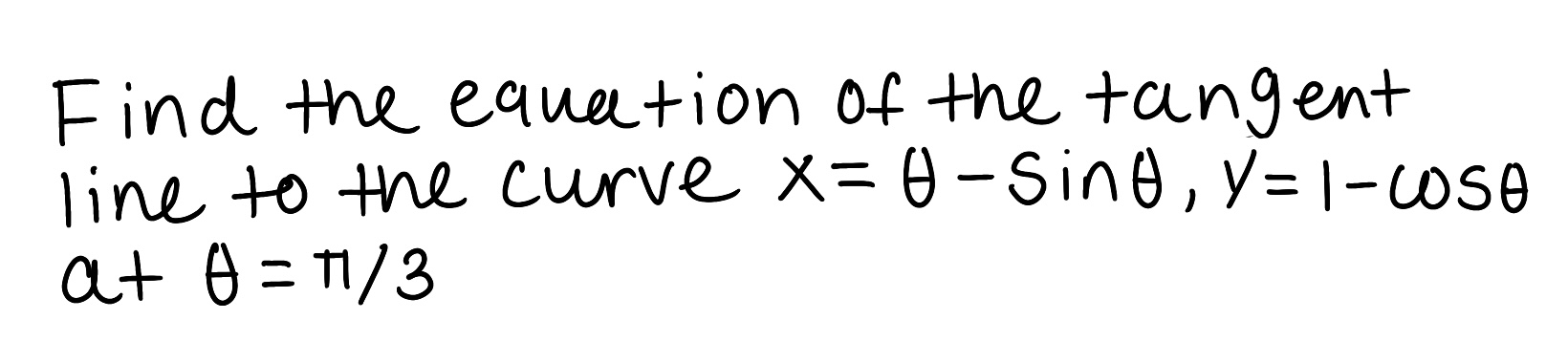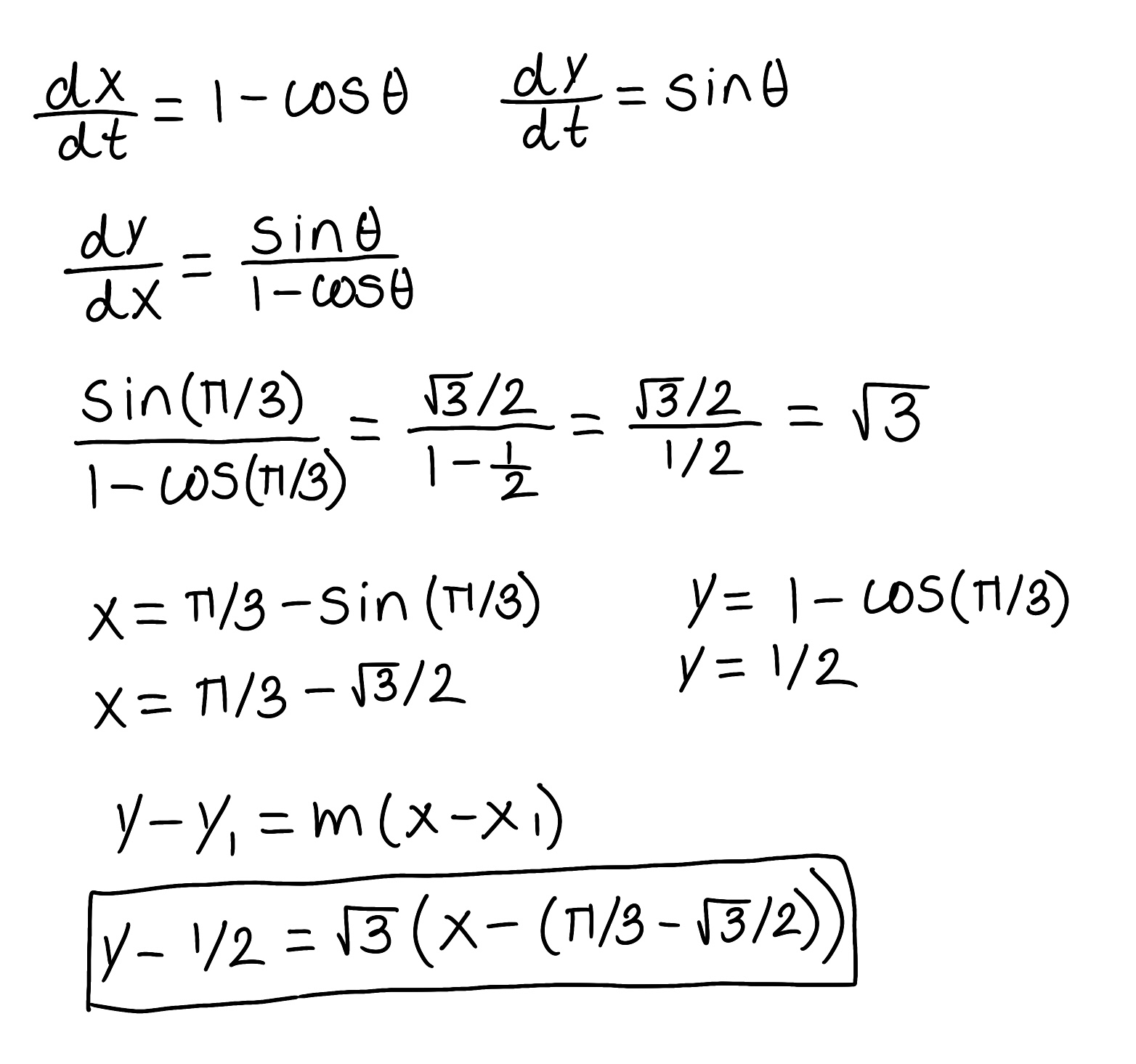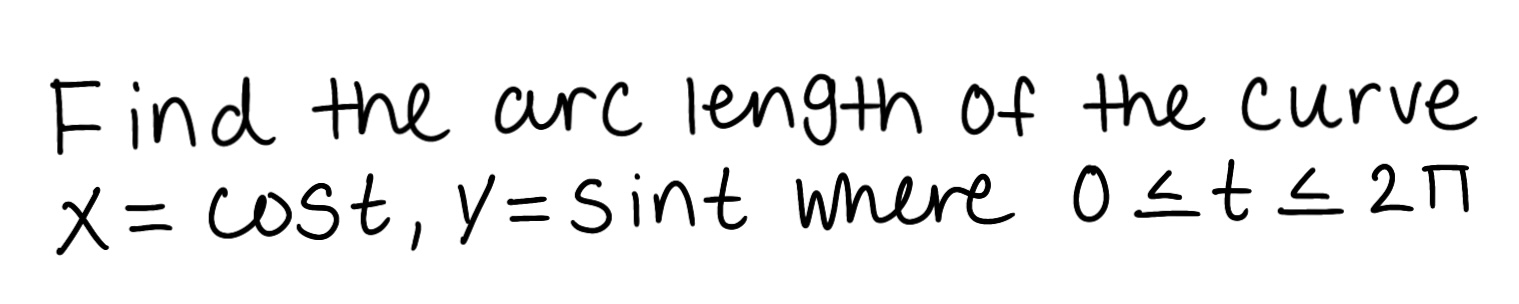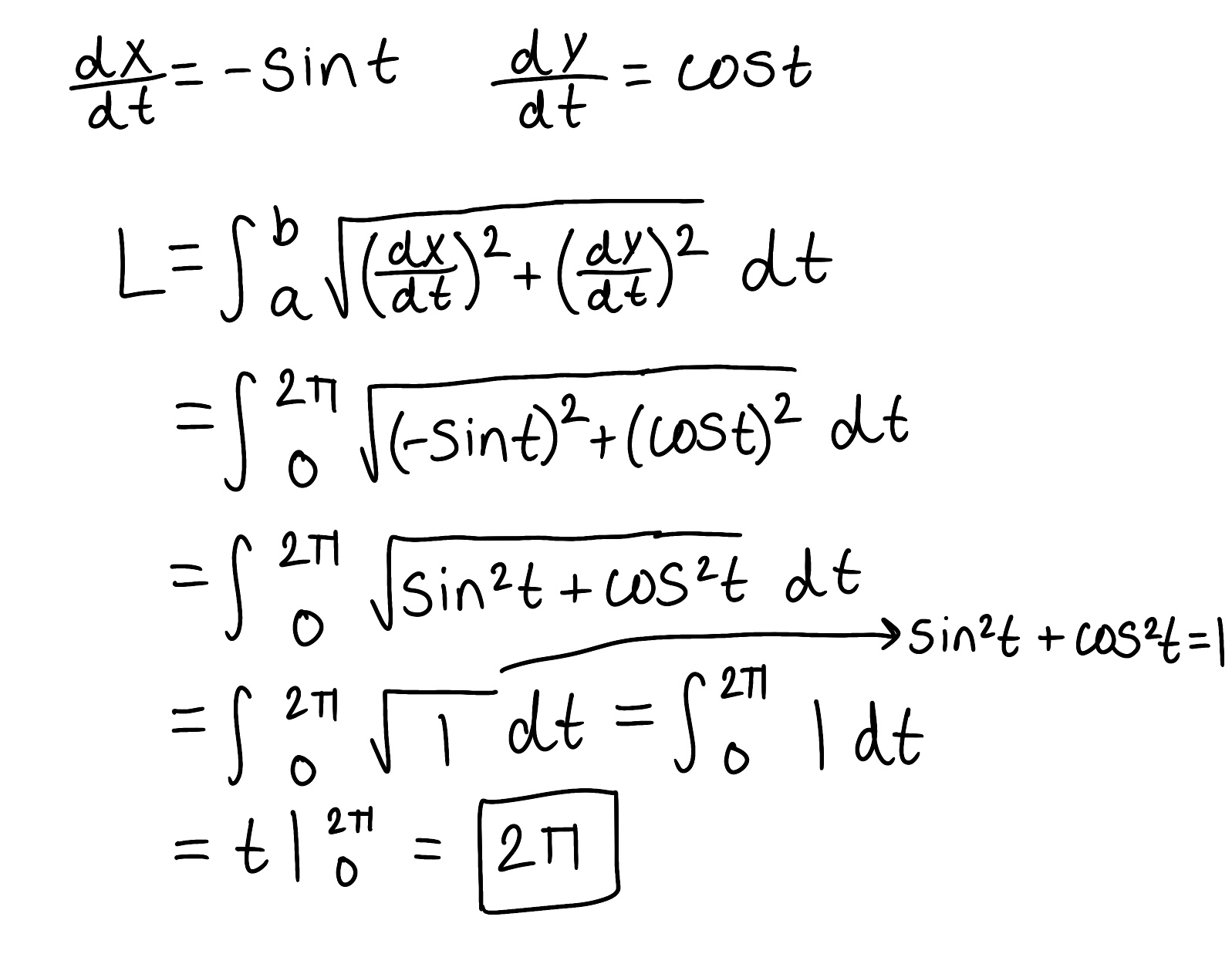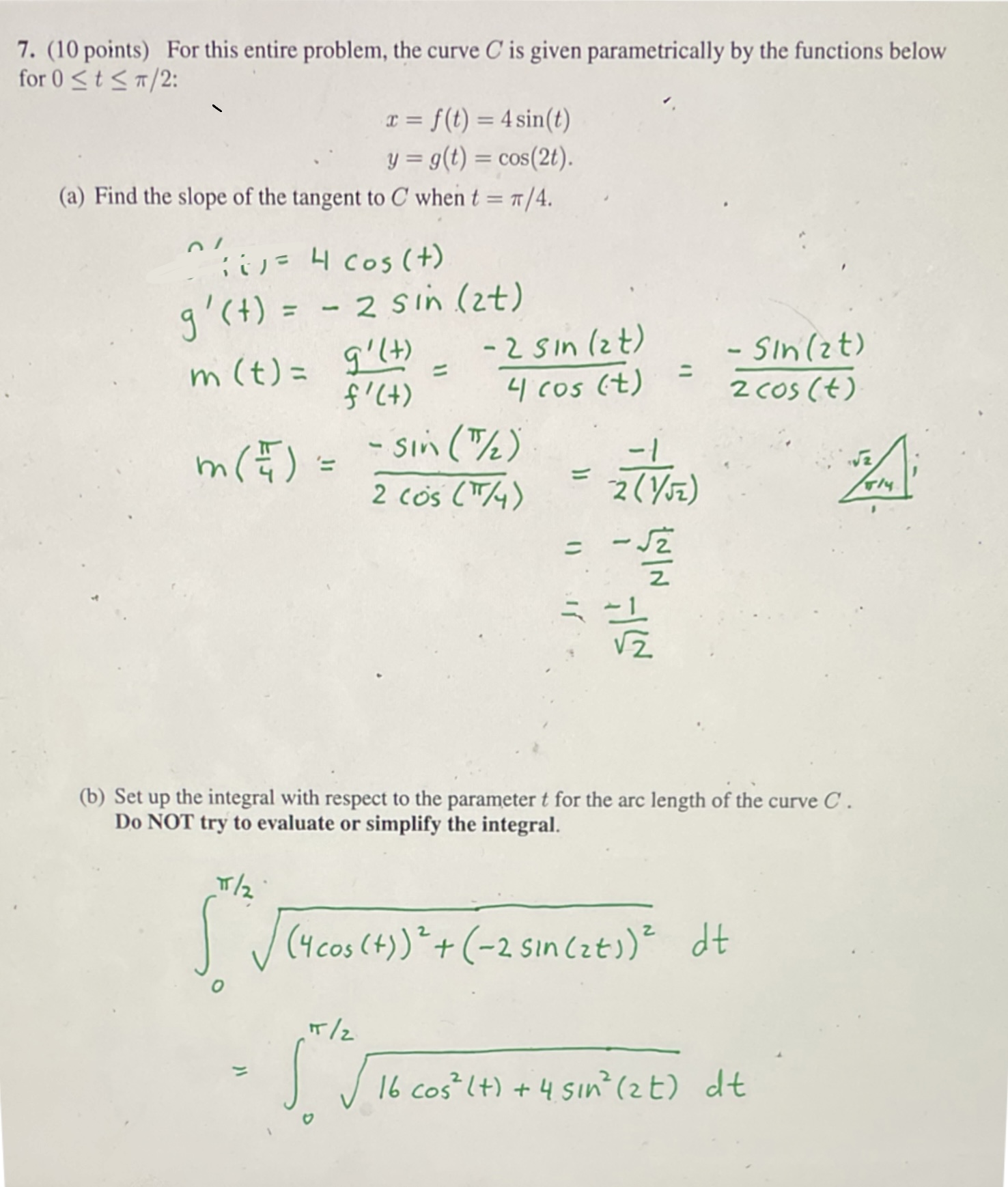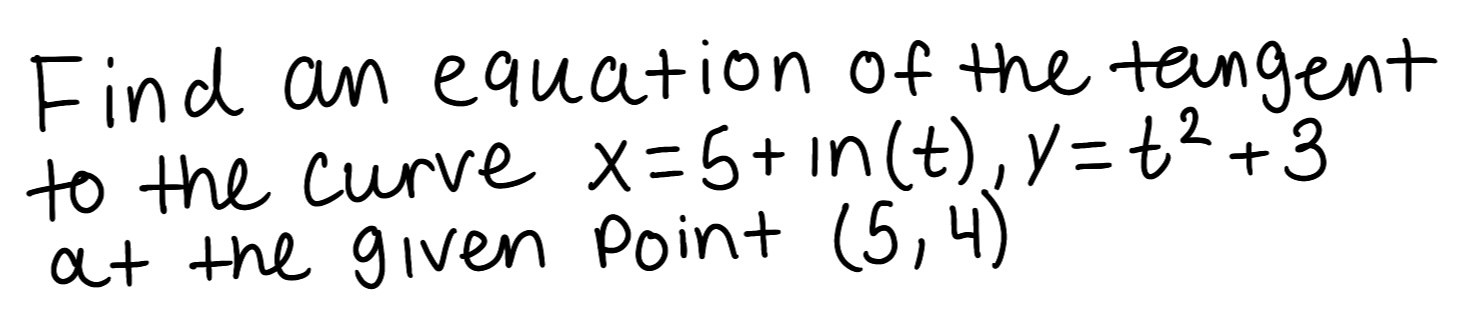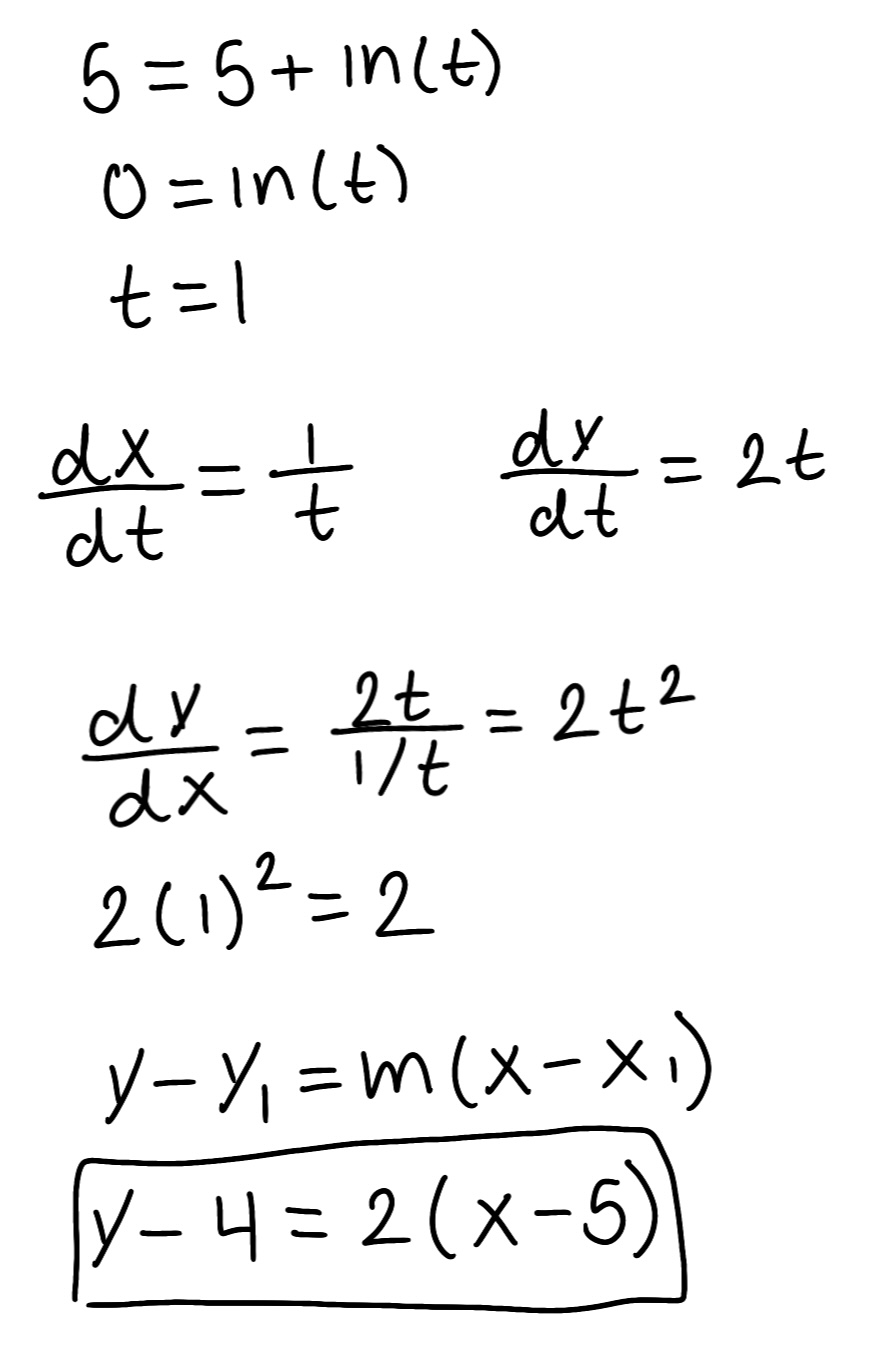MATH 226 - Final Review

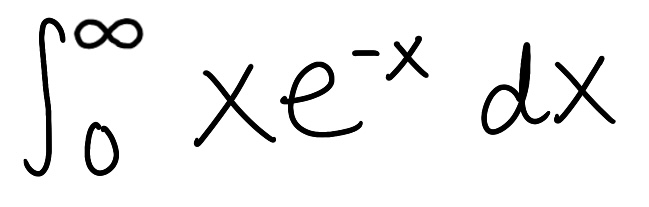
• Evaluate the integral

• Explain why the integral is improper

• Determine if the integral converges or diverges and explain why

• The integral is improper because one of the bounds is infinite

• The integral converges because the limit is finite

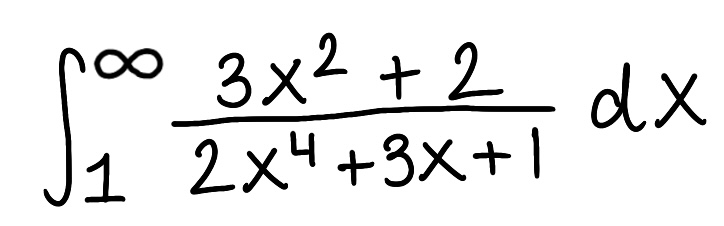
Use the Comparison Theorem to determine if the improper integral converges or diverges (do not evaluate the integral)

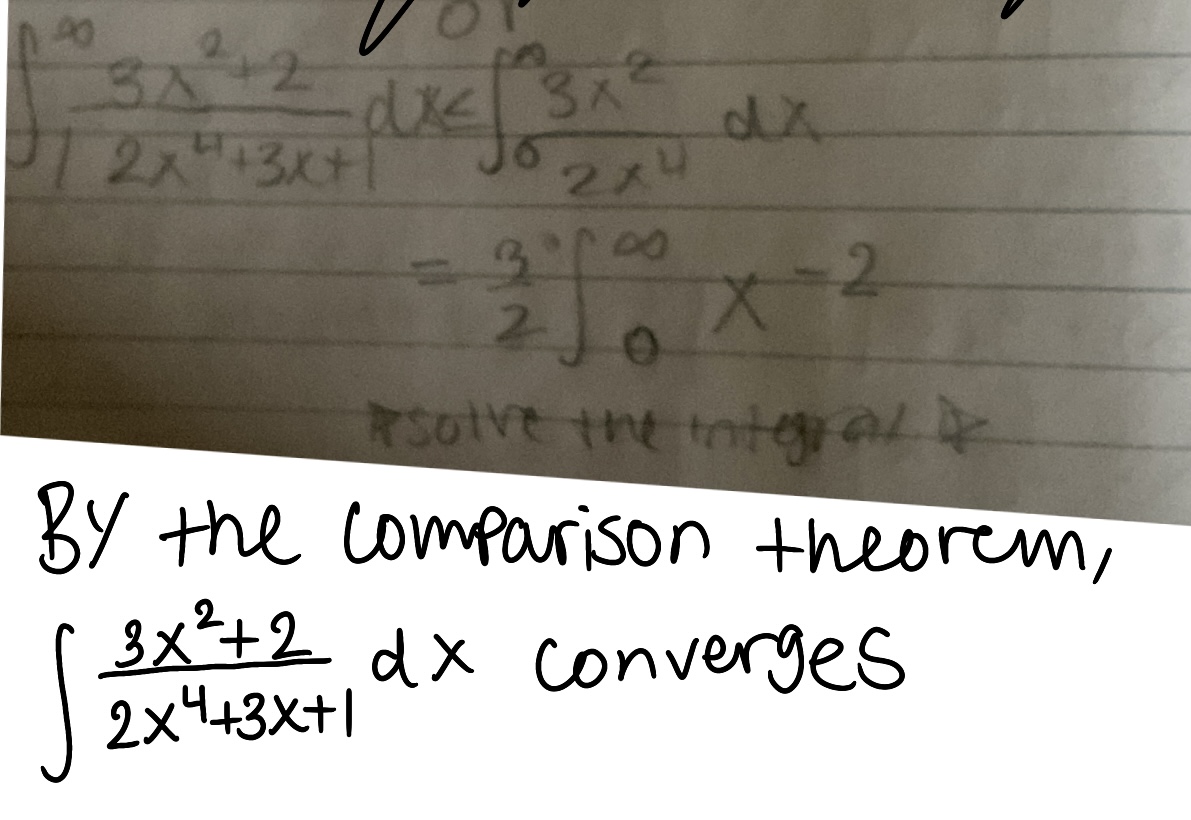
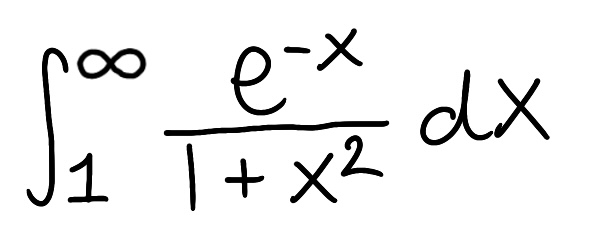
Use the Comparison Theorem to determine if the improper integral converges or diverges (do not evaluate the integral)

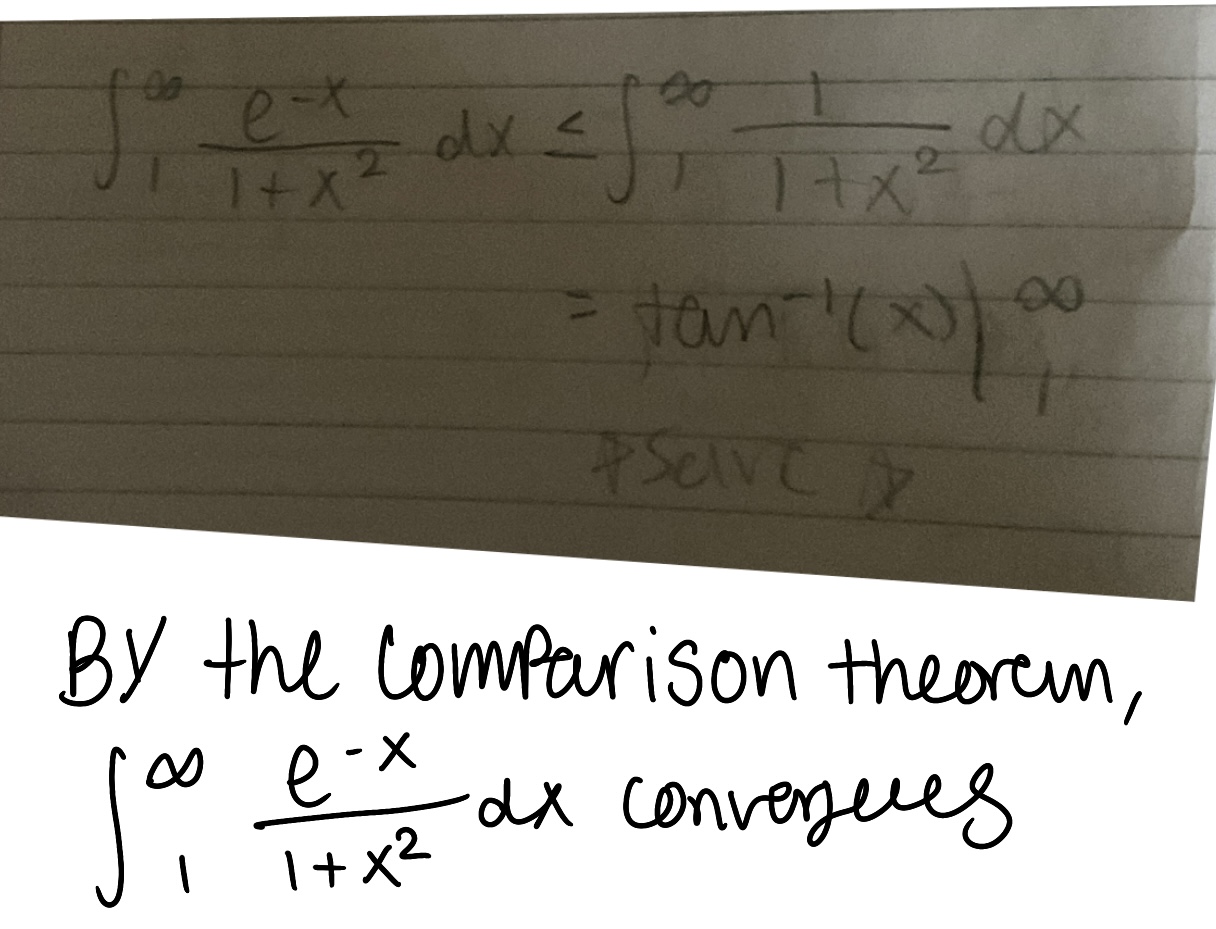
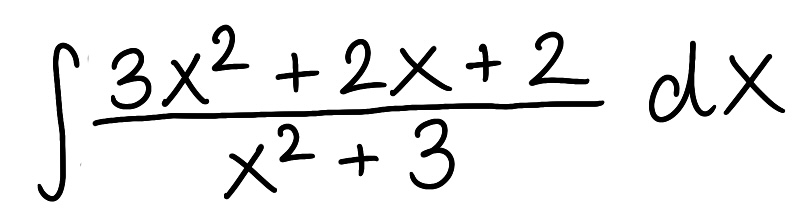
Evaluate the Integral

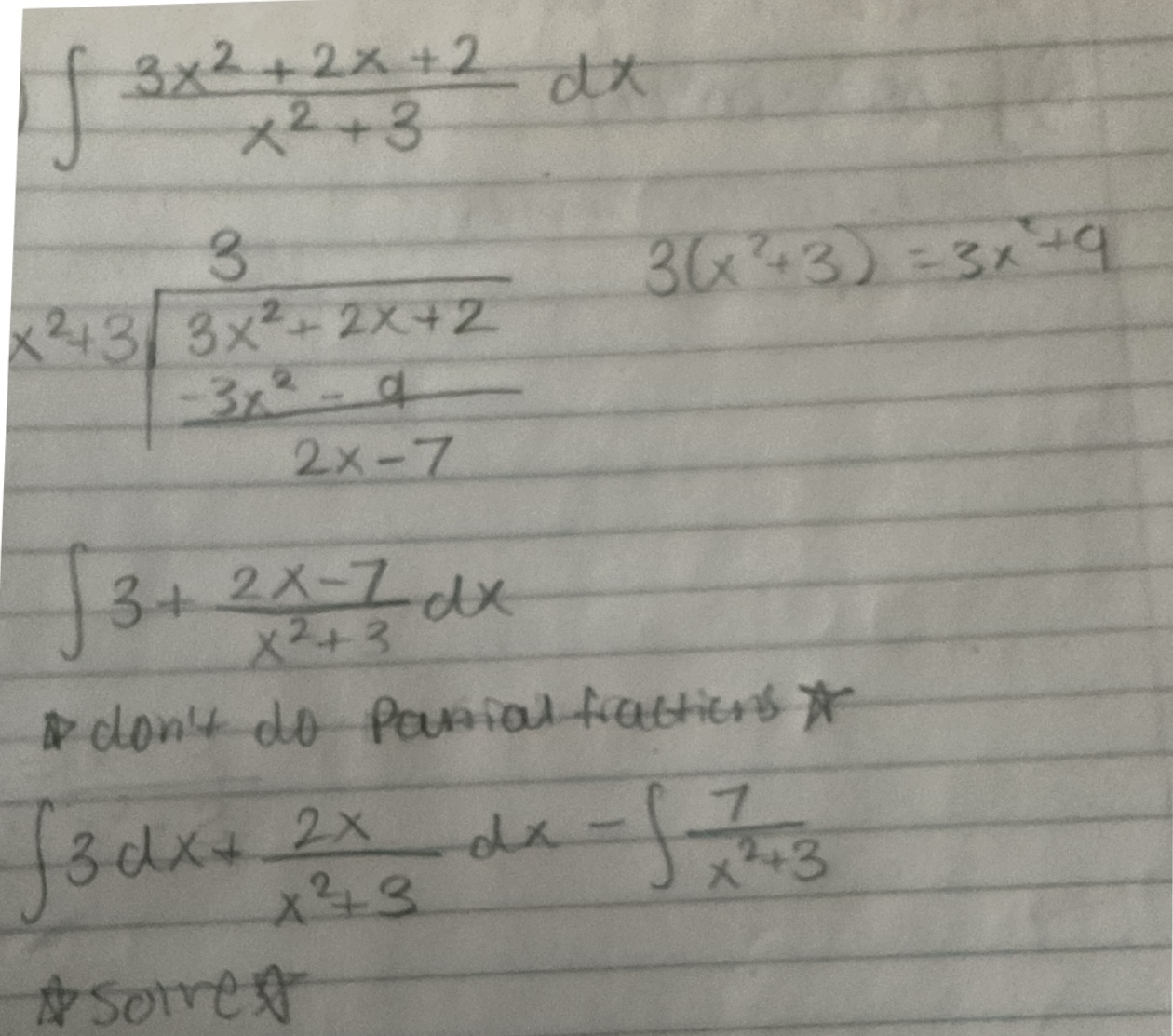
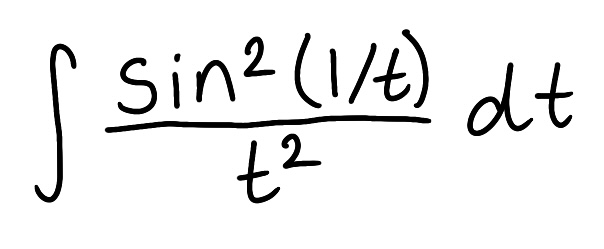
Evaluate the integral

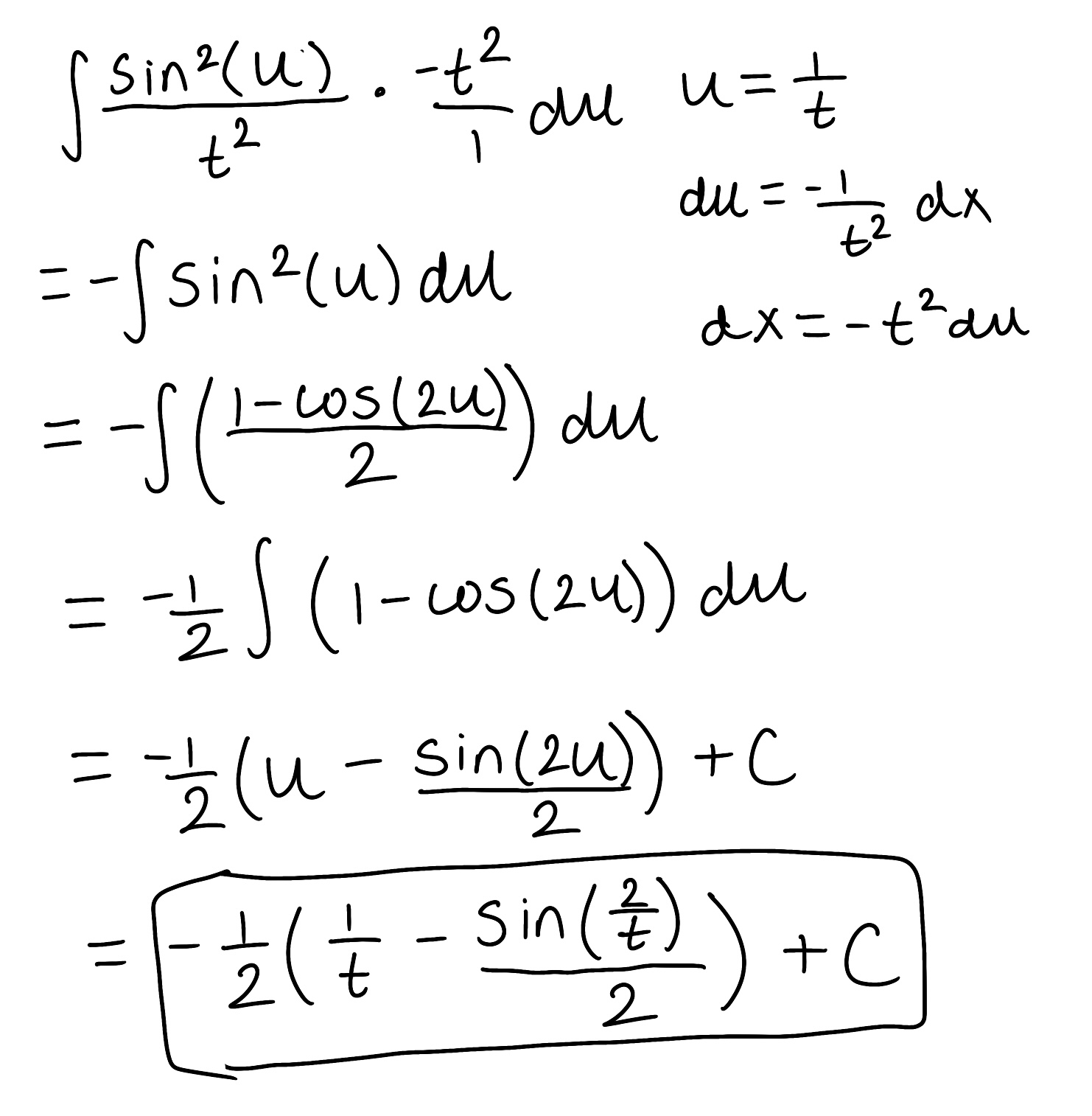
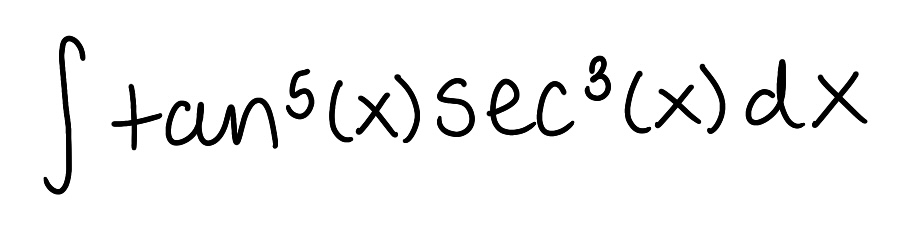
Evaluate the integral

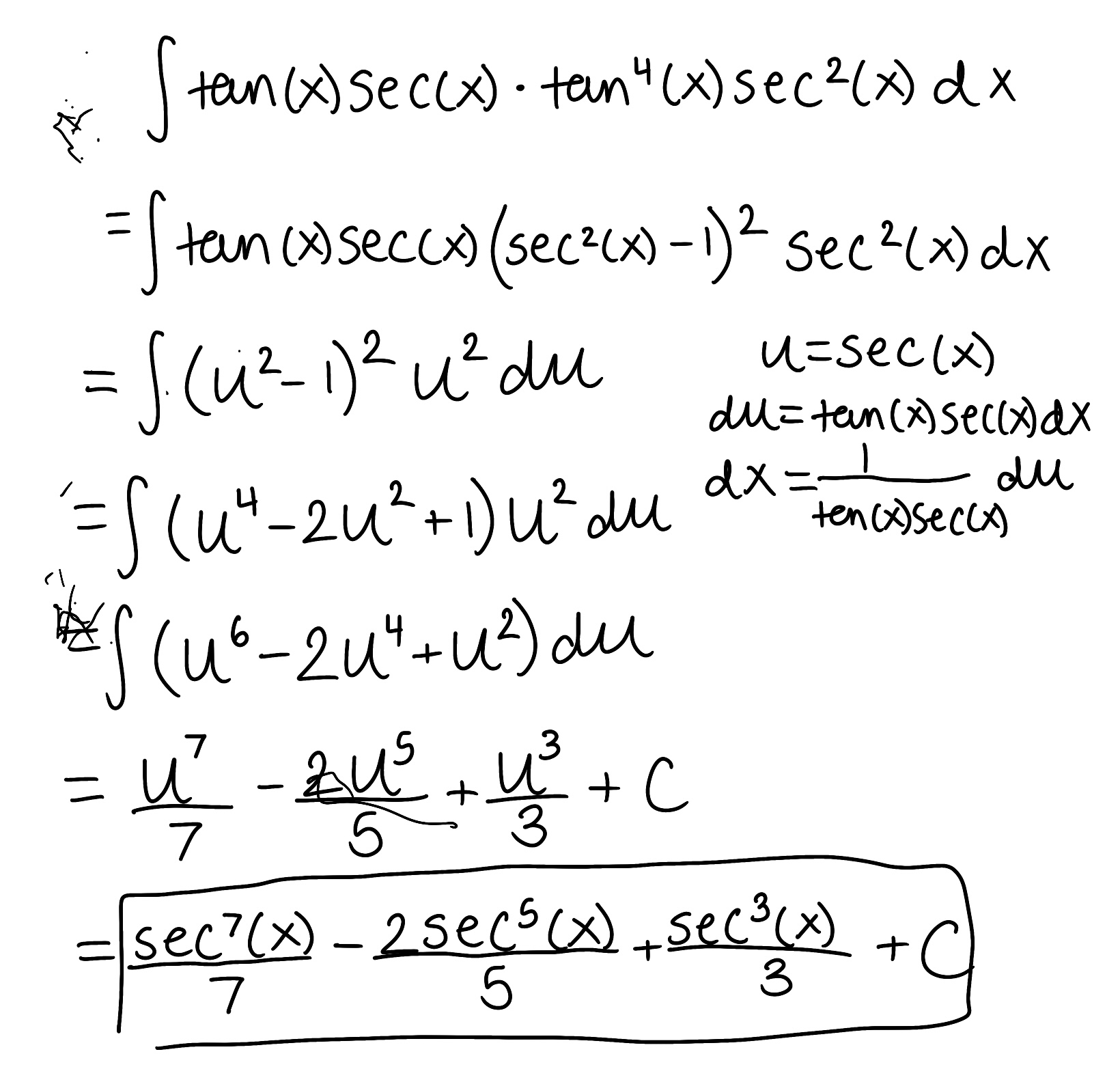
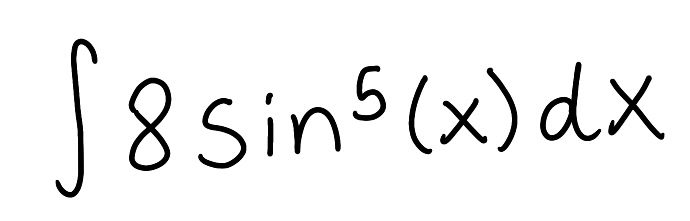
Evaluate the integral

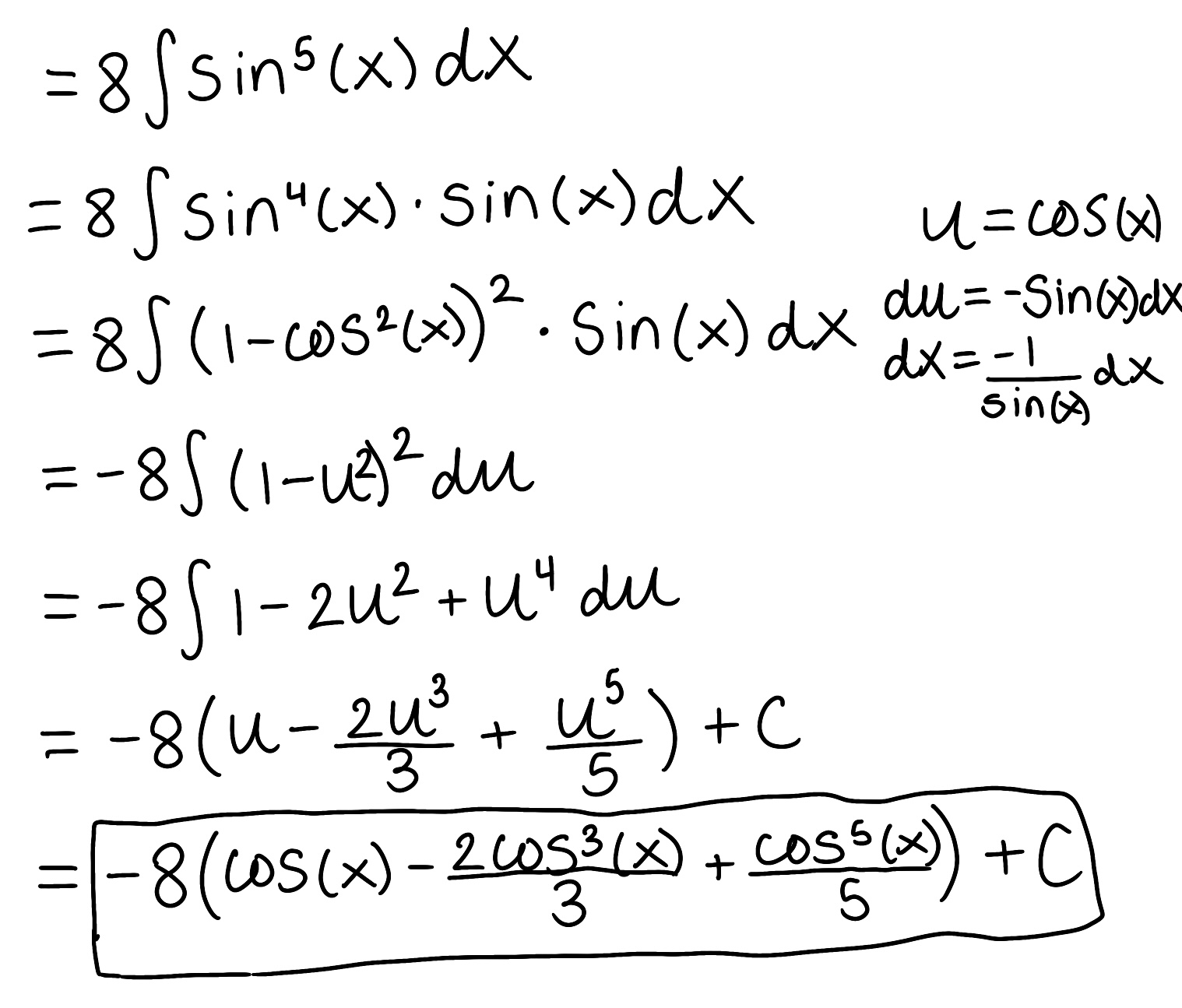
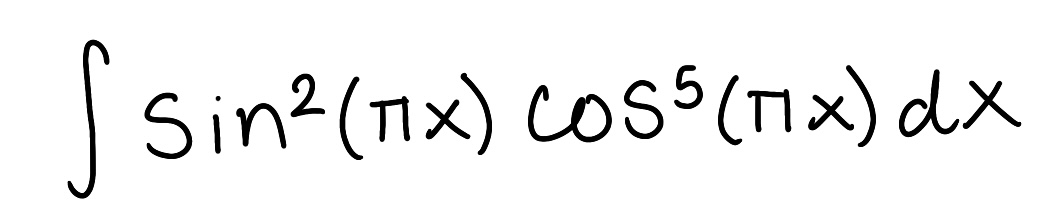
Evaluate the integral

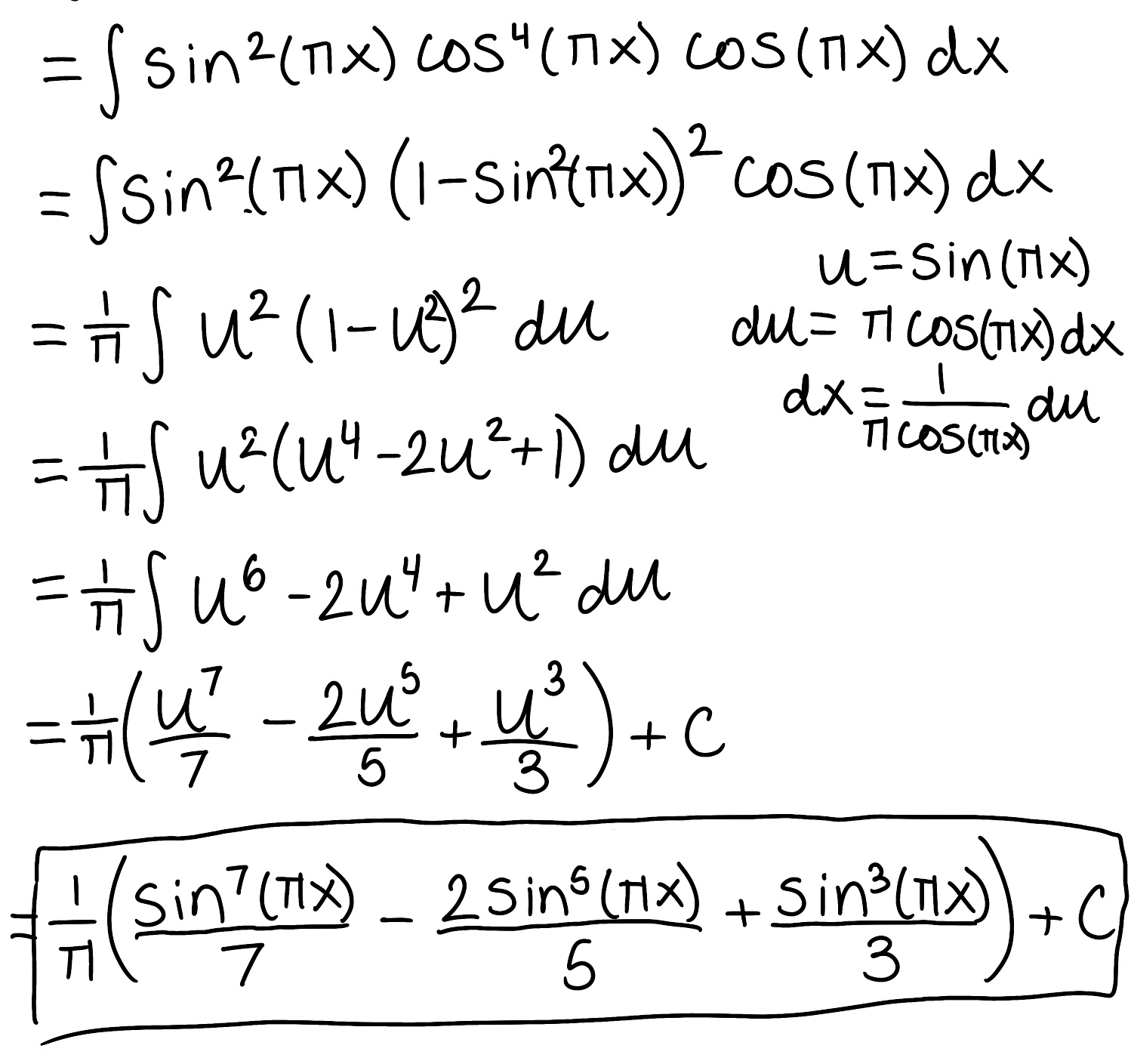
Evaluate the integral

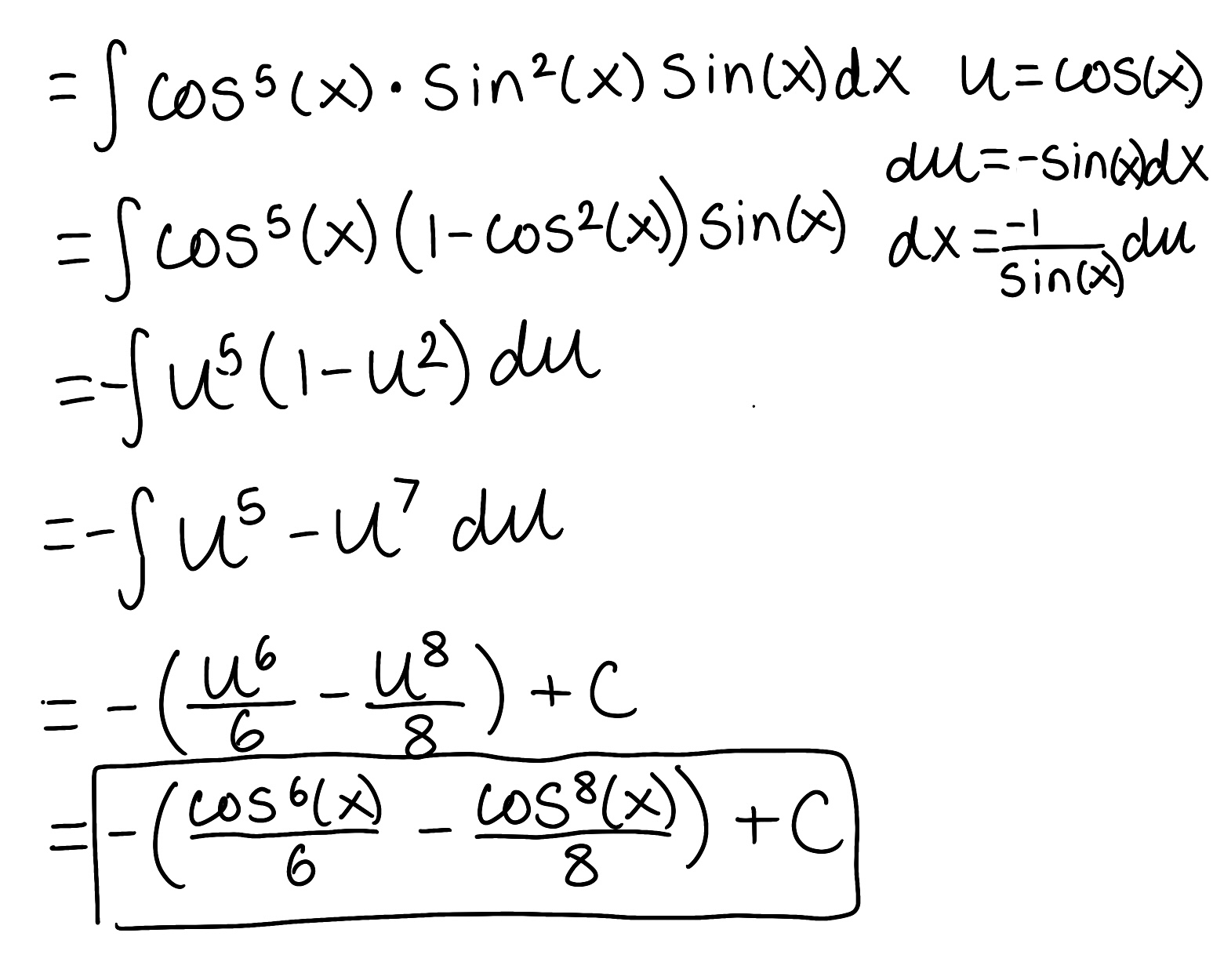
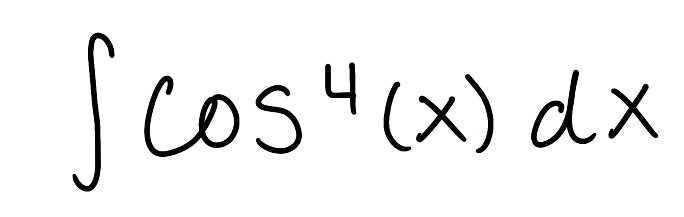
Evaluate the integral

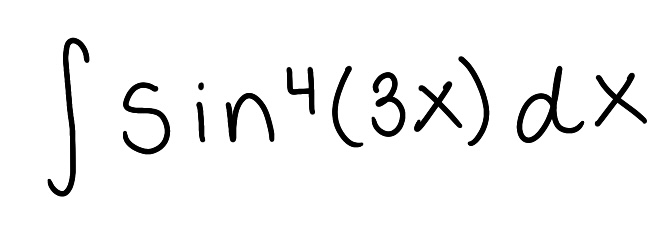
Evaluate the integral

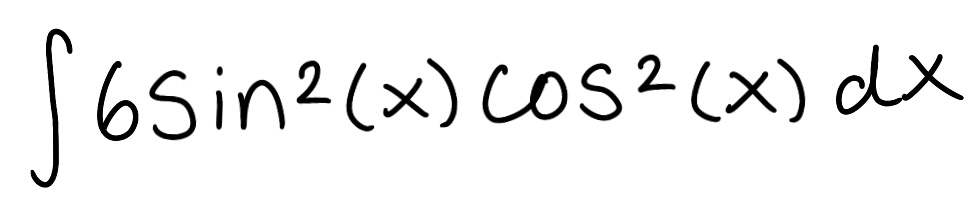
Evaluate the integral (stop right before you start integrating)

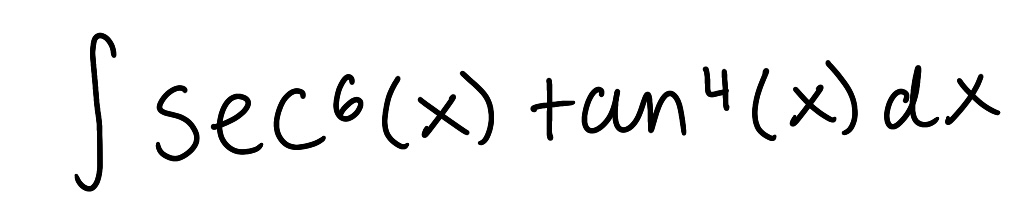
Evaluate the integral

Evaluate the integral

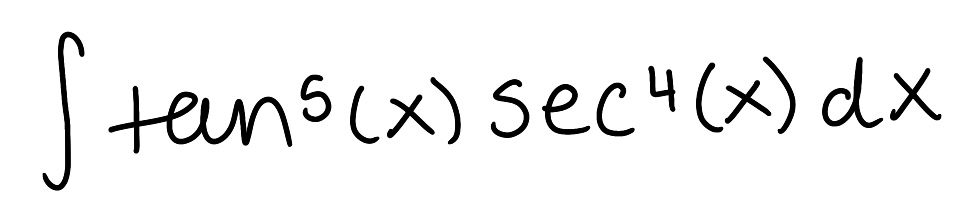
Evaluate the integral

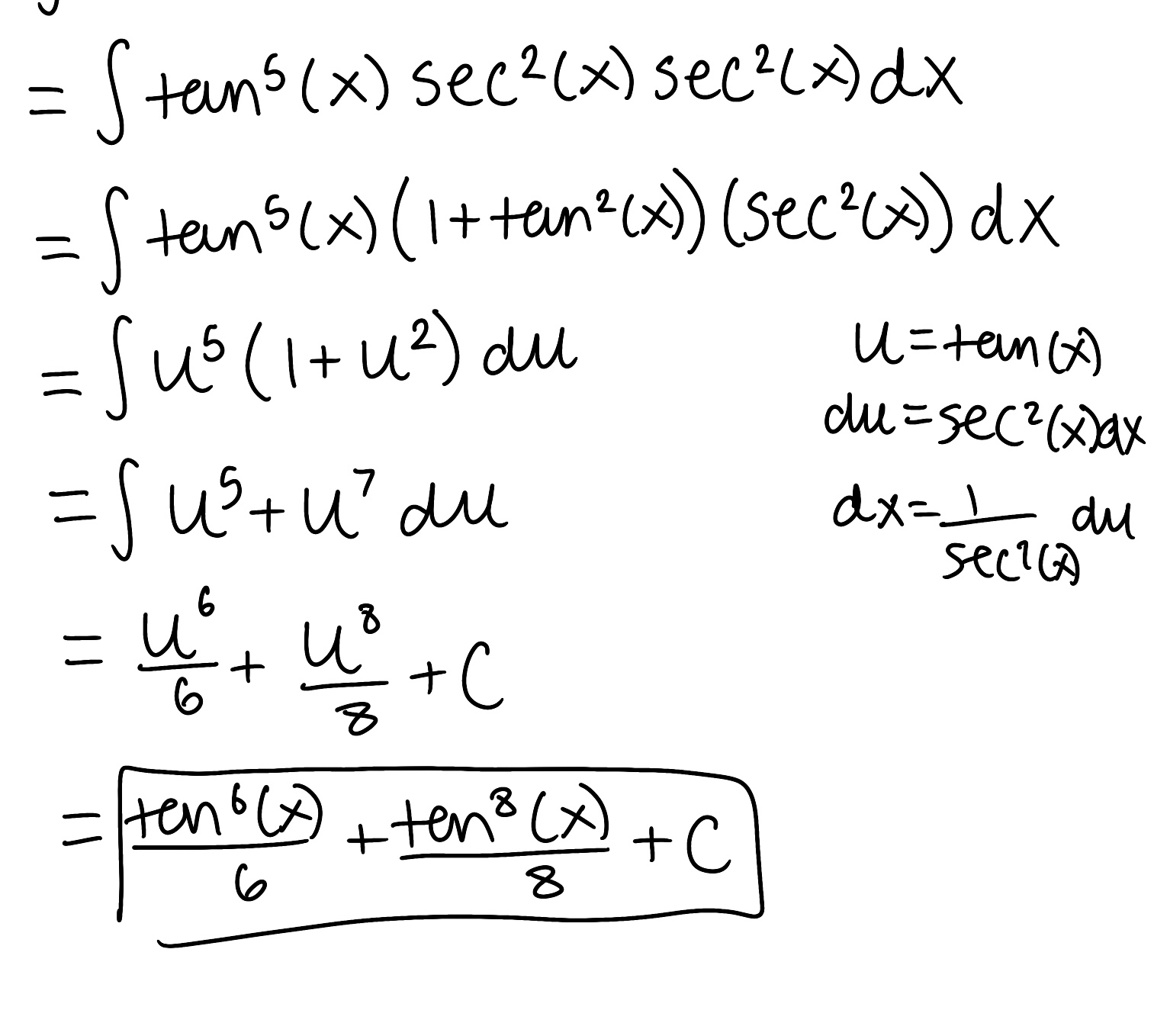
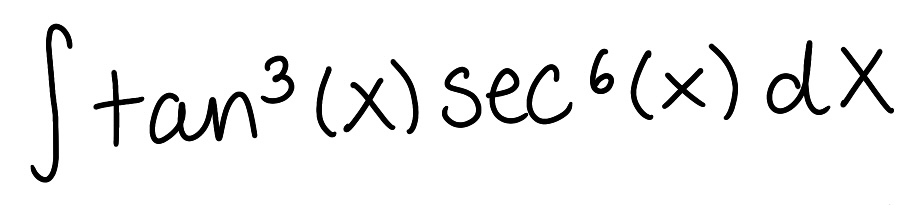
Evaluate the integral

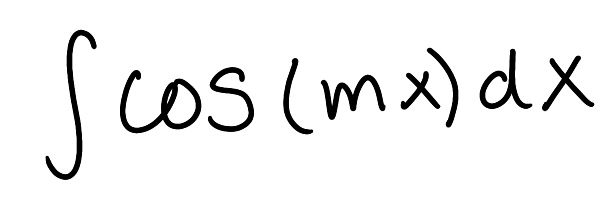
Evaluate the integral

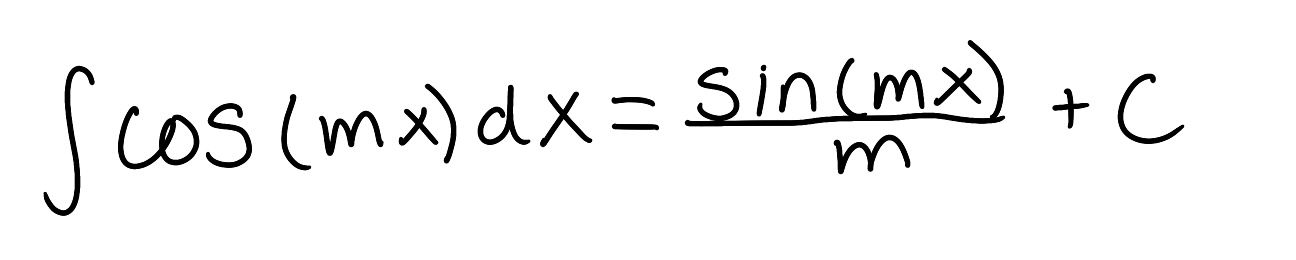
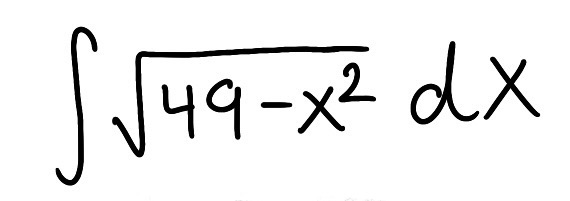
Evaluate the integral

The answer should have √(49-x²)

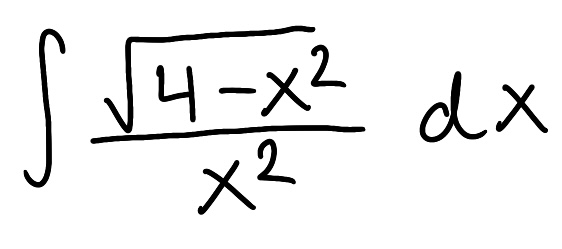
Evaluate the integral

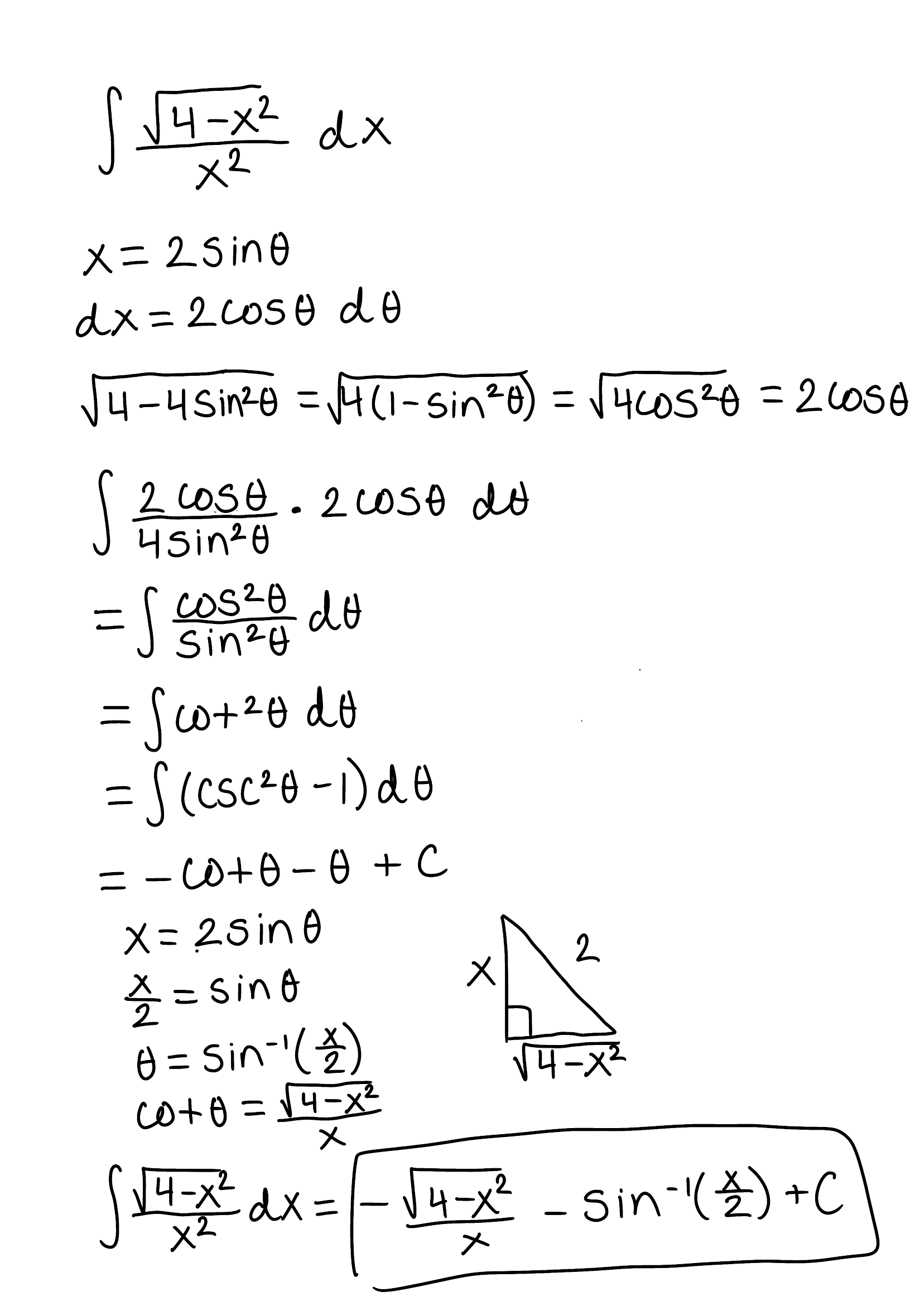
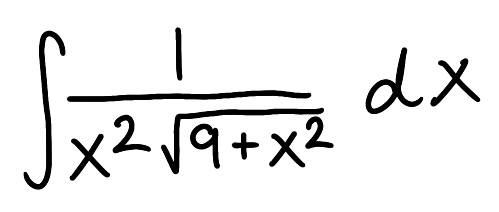
Evaluate the integral

The answer should have √(9+x²)

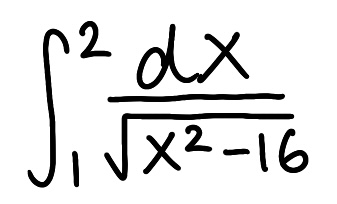
Evaluate the integral

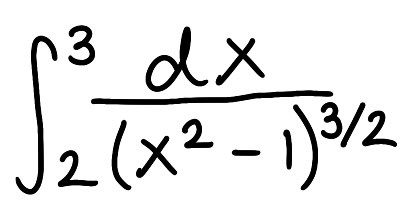
Evaluate the integral

Only change the bounds when doing u sub for cosx/sin²x

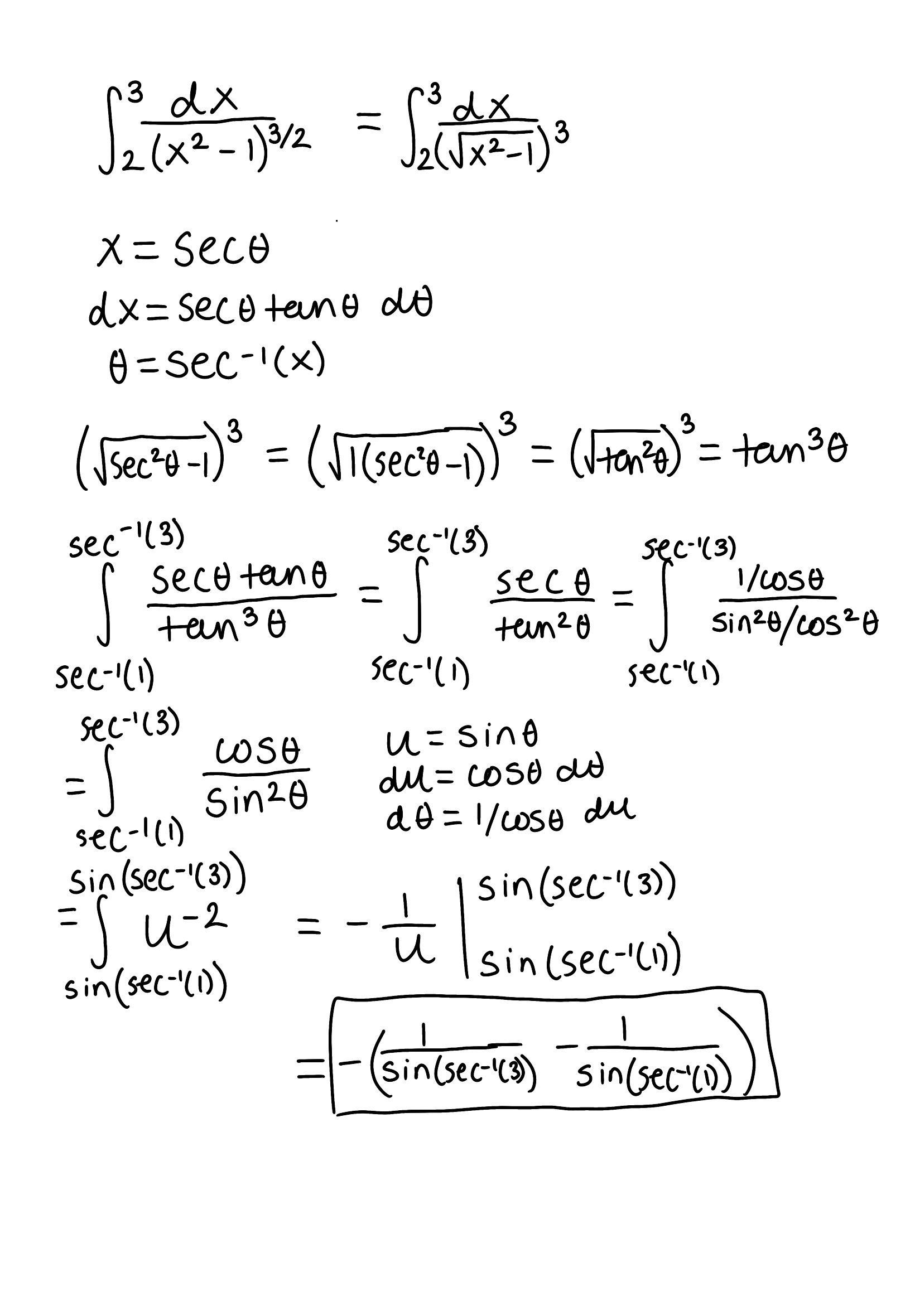
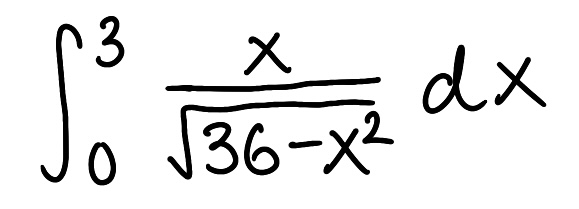
Evaluate the integral

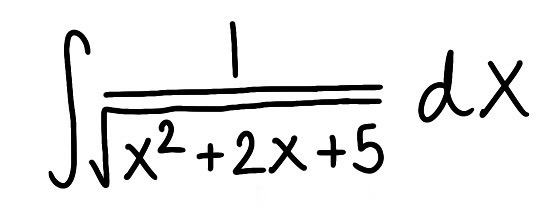
Evaluate the integral

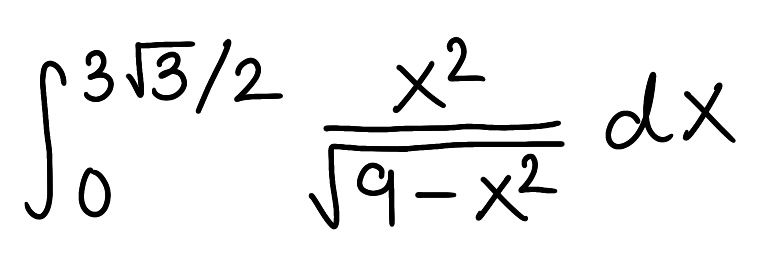
Evaluate the integral

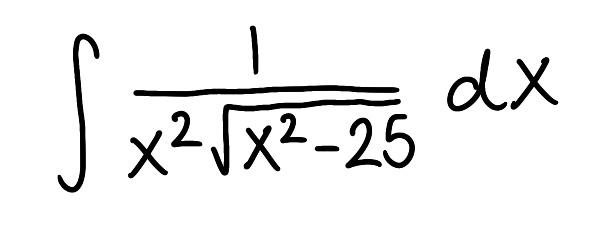
Evaluate the integral

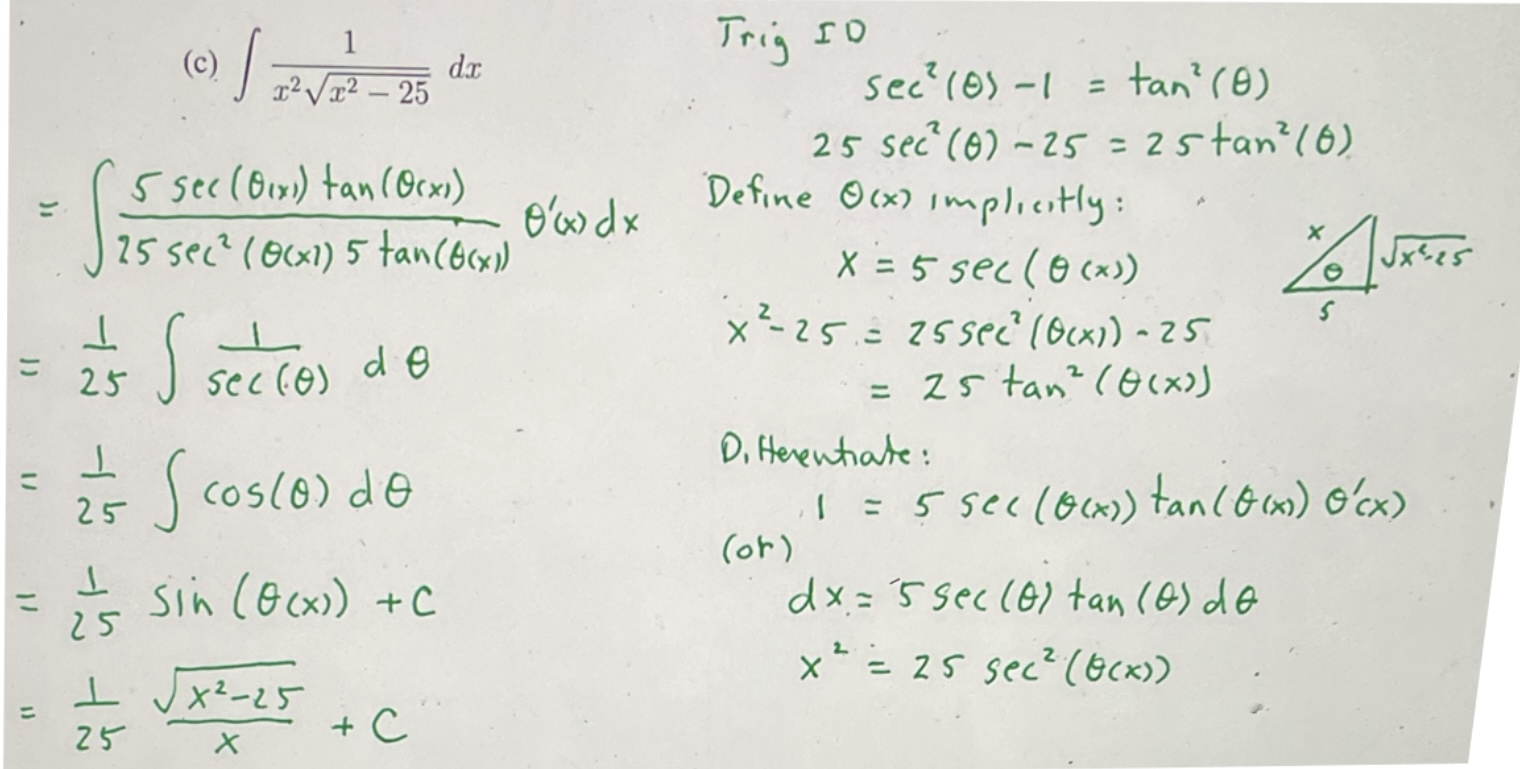
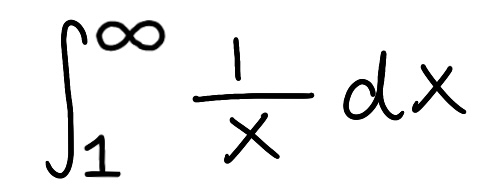
• Evaluate the integral

• Explain why the integral is improper

• Determine if the integral converges or diverges and explain why

• The integral is improper because one of the bounds is infinite

• The integral diverges because the limit is infinite

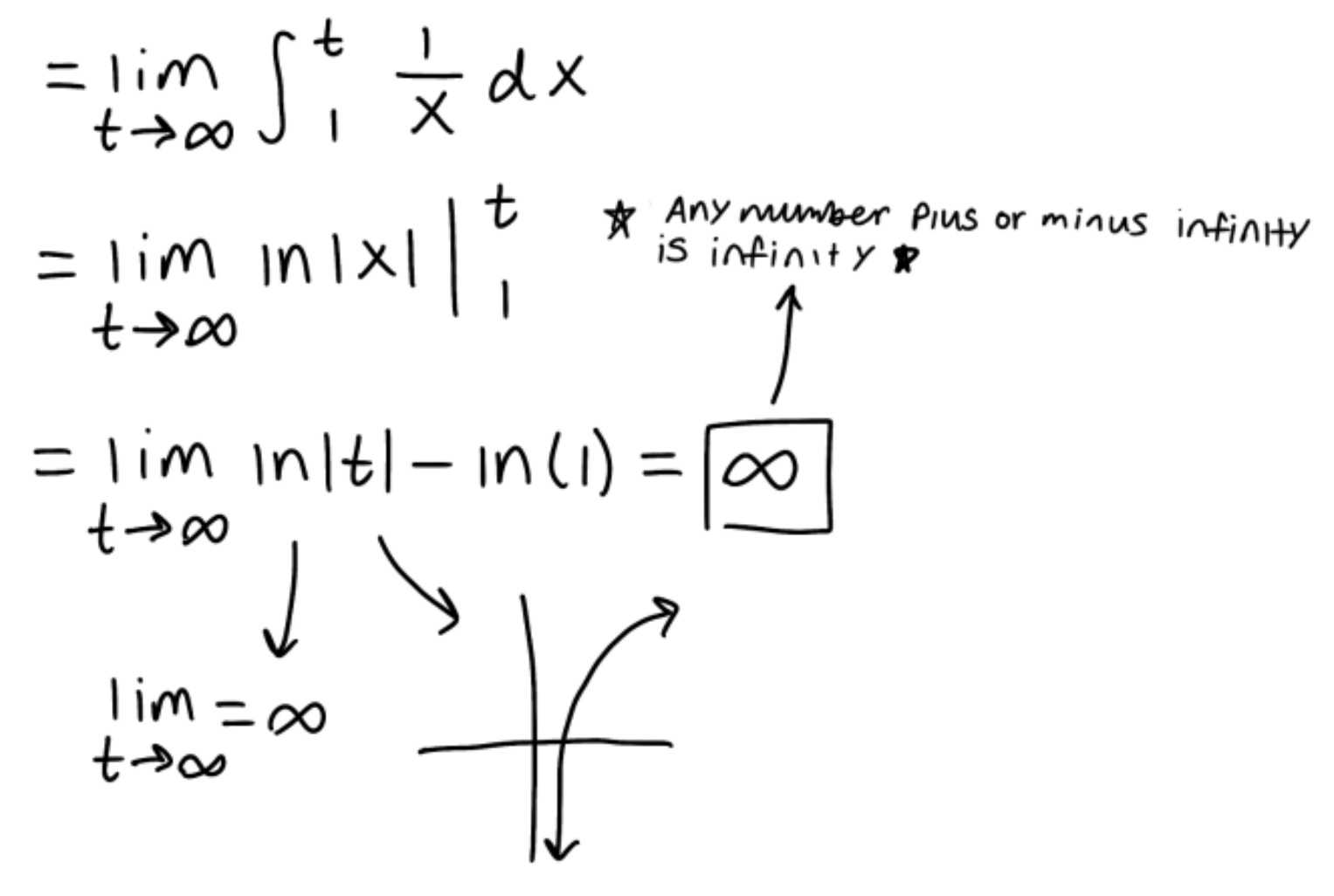
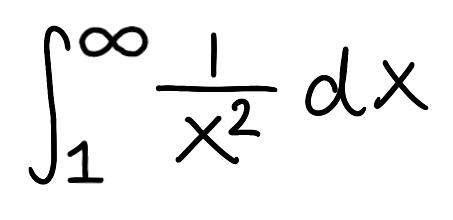
• Evaluate the integral

• Explain why the integral is improper

• Determine if the integral converges or diverges and explain why

• The integral is improper because one of the bounds is infinite

• The integral converges because the limit is finite

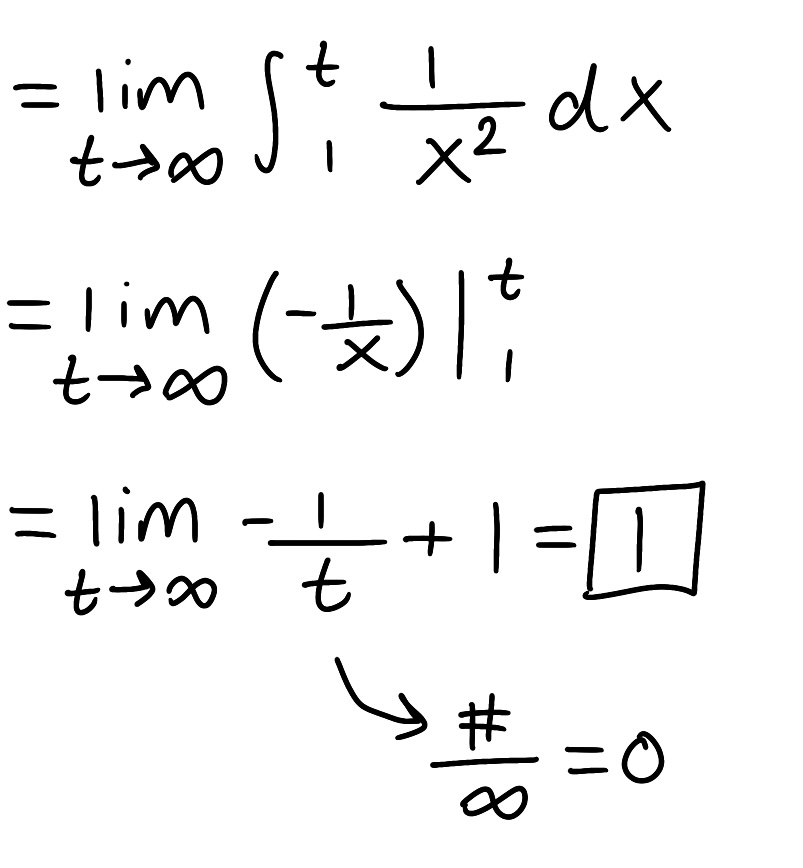
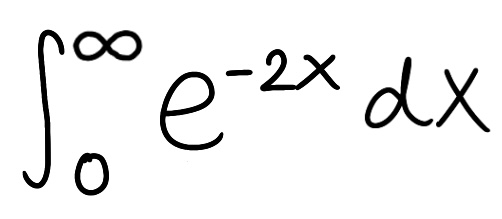
• Evaluate the integral

• Explain why the integral is improper

• Determine if the integral converges or diverges and explain why

• The integral is improper because one of the bounds is infinite

• The integral converges because the limit is finite

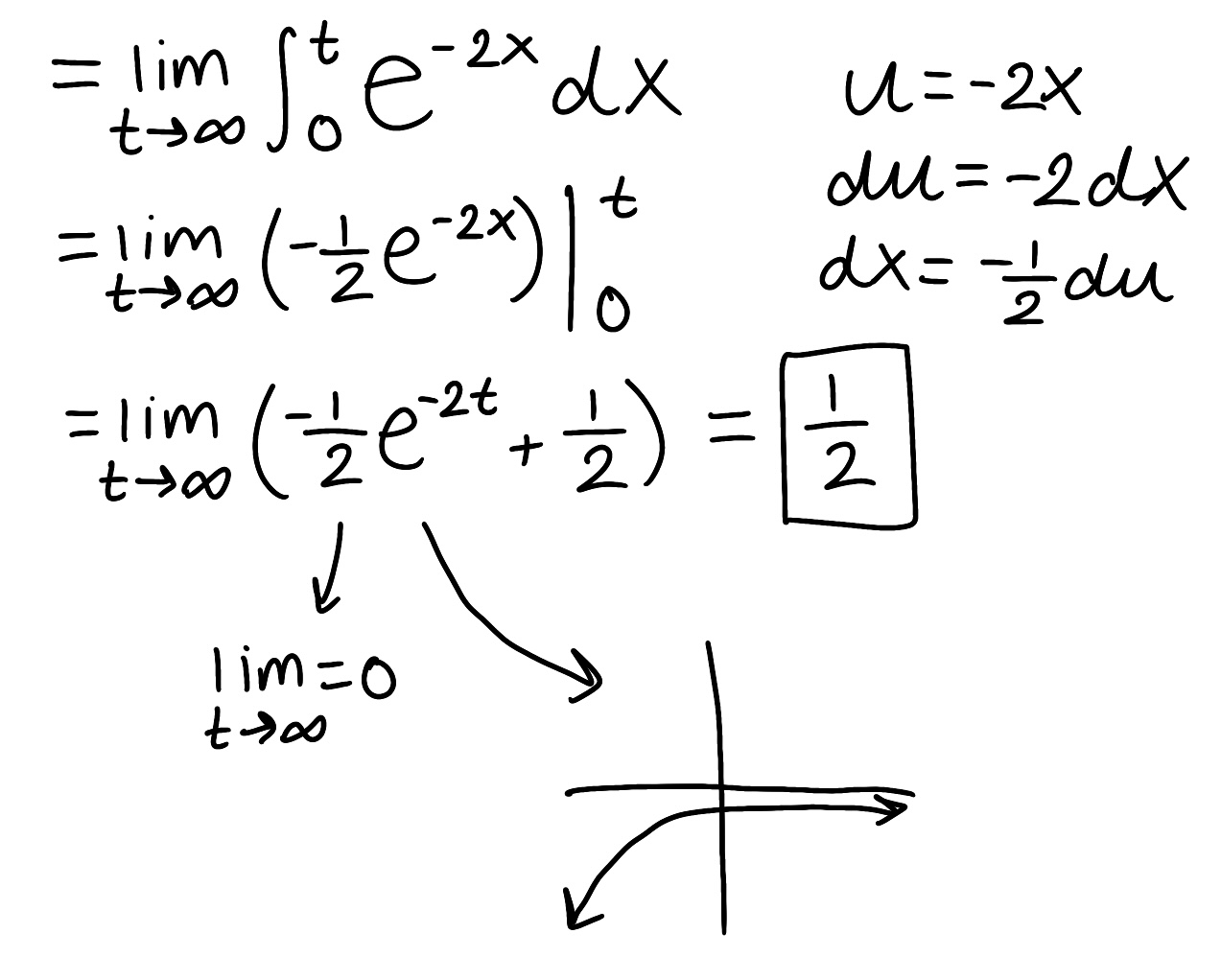
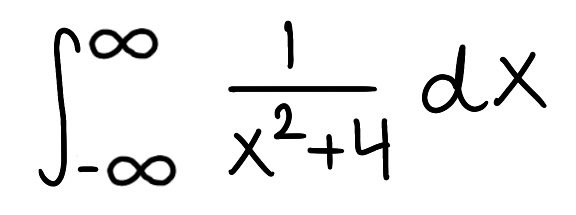
• Evaluate the integral

• Explain why the integral is improper

• Determine if the integral converges or diverges and explain why

• The integral is improper because both of the bounds are infinite

• The integral converges because the limit is finite

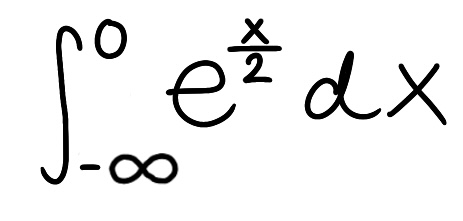
• Evaluate the integral

• Explain why the integral is improper

• Determine if the integral converges or diverges and explain why

• The integral is improper because one of the bounds is infinite

• The integral converges because the limit is finite

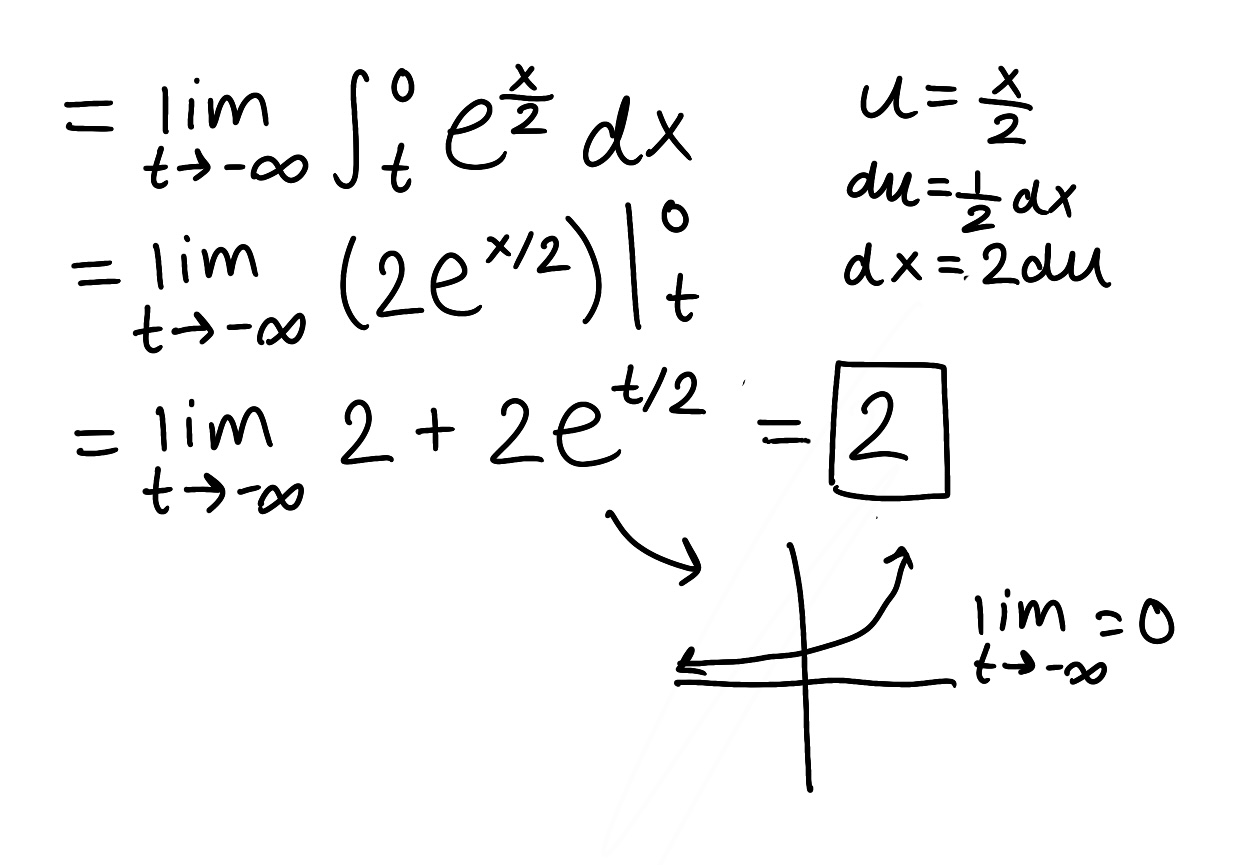
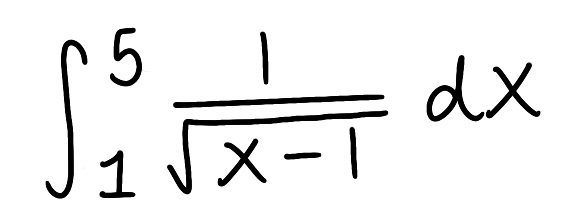
• Evaluate the integral

• Explain why the integral is improper

• Determine if the integral converges or diverges and explain why

• The integral is improper because there is a discontinuity x=1

• The integral converges because the limit is finite

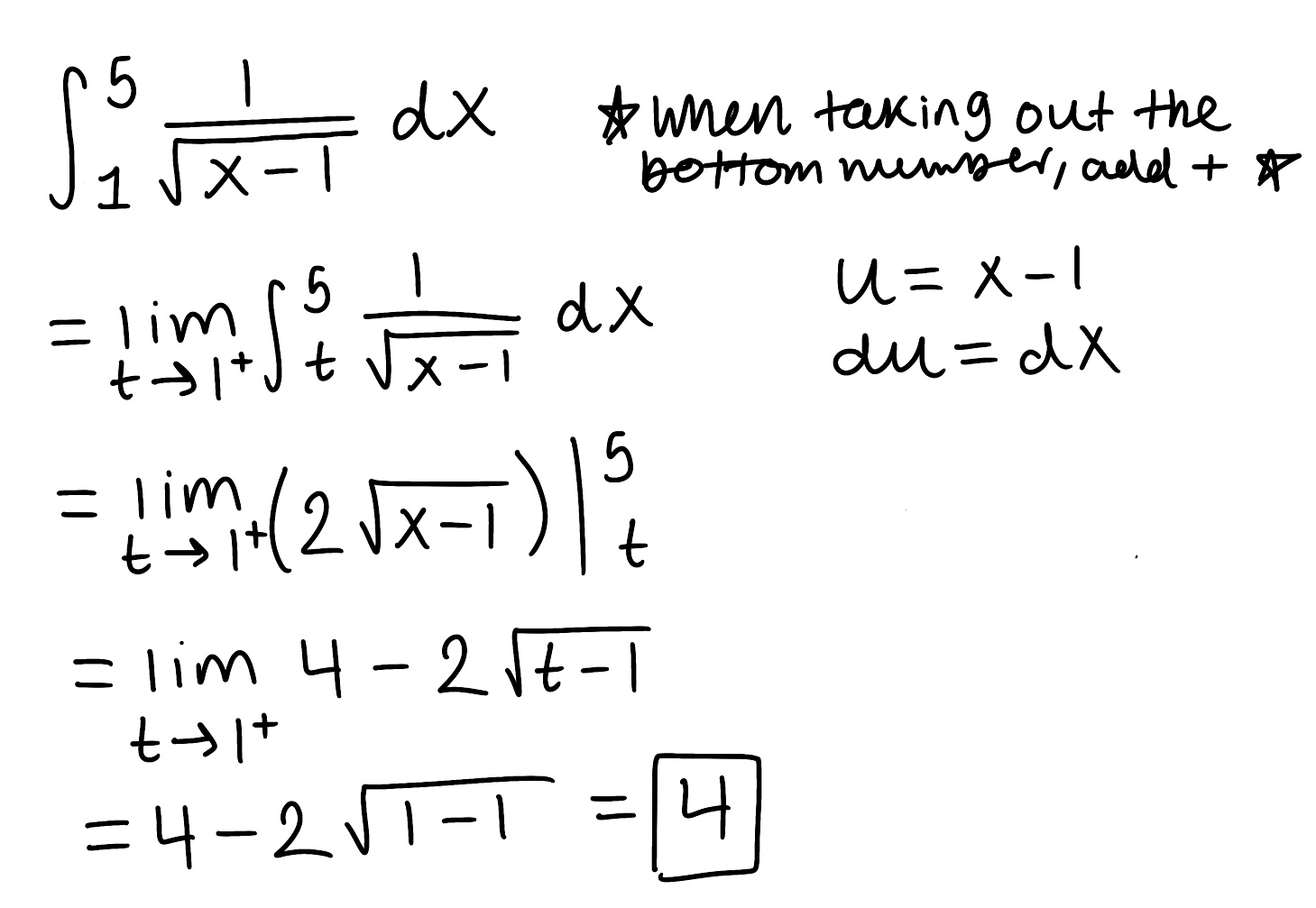
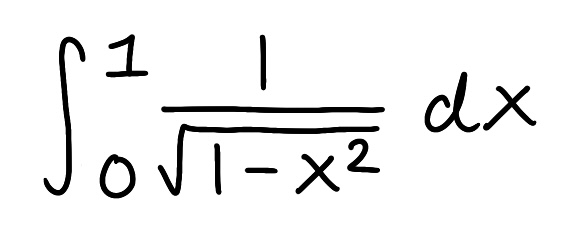
• Evaluate the integral

• Explain why the integral is improper

• Determine if the integral converges or diverges and explain why

• The integral is improper because there is a discontinuity x=1

• The integral converges because the limit is finite

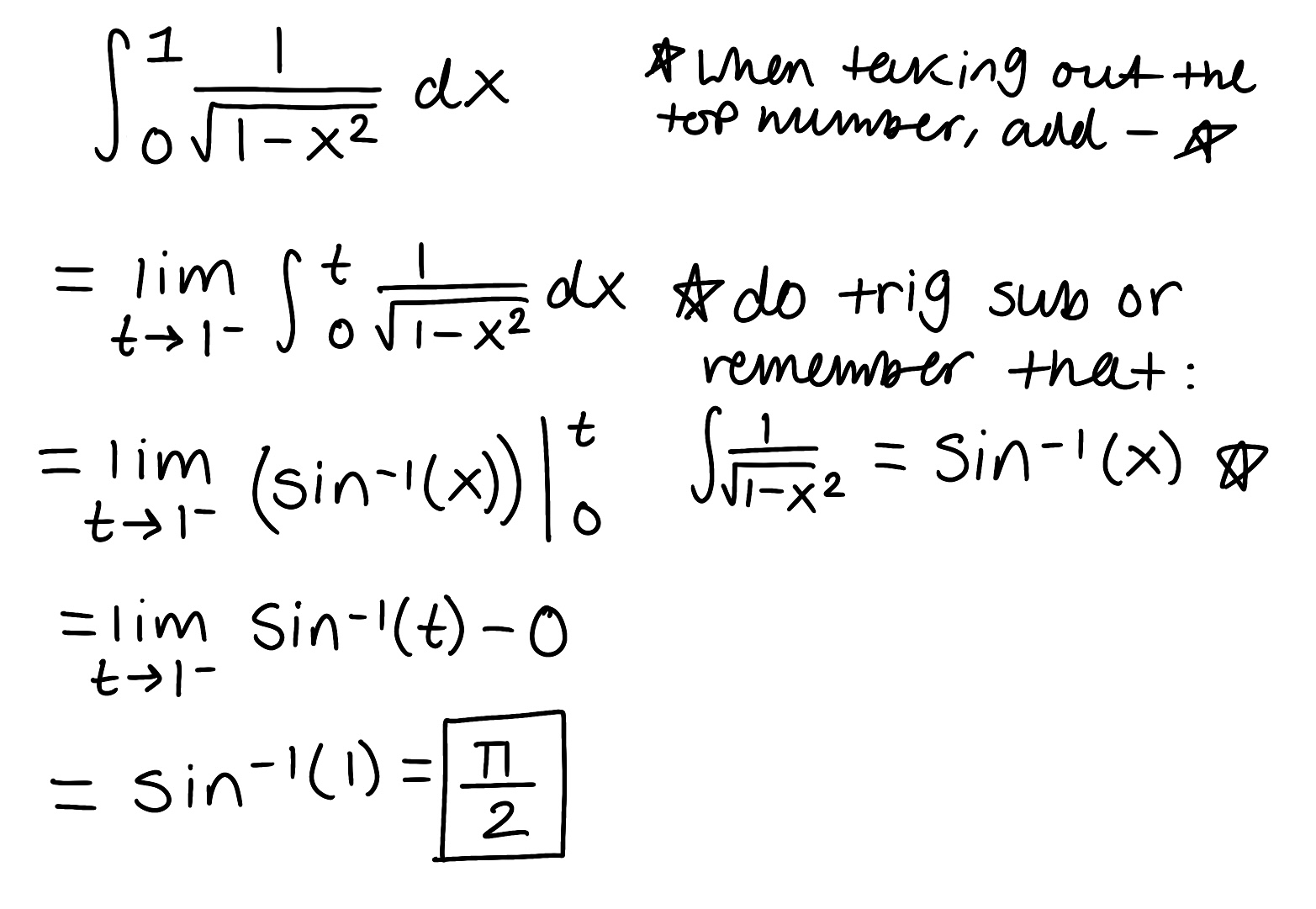
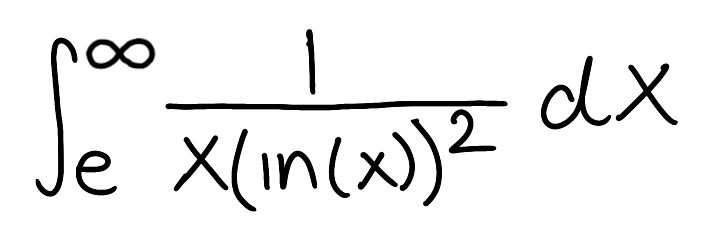
• Evaluate the integral

• Explain why the integral is improper

• Determine if the integral converges or diverges and explain why

• The integral is improper because one of the bounds is infinite

• The integral converges because the limit is finite

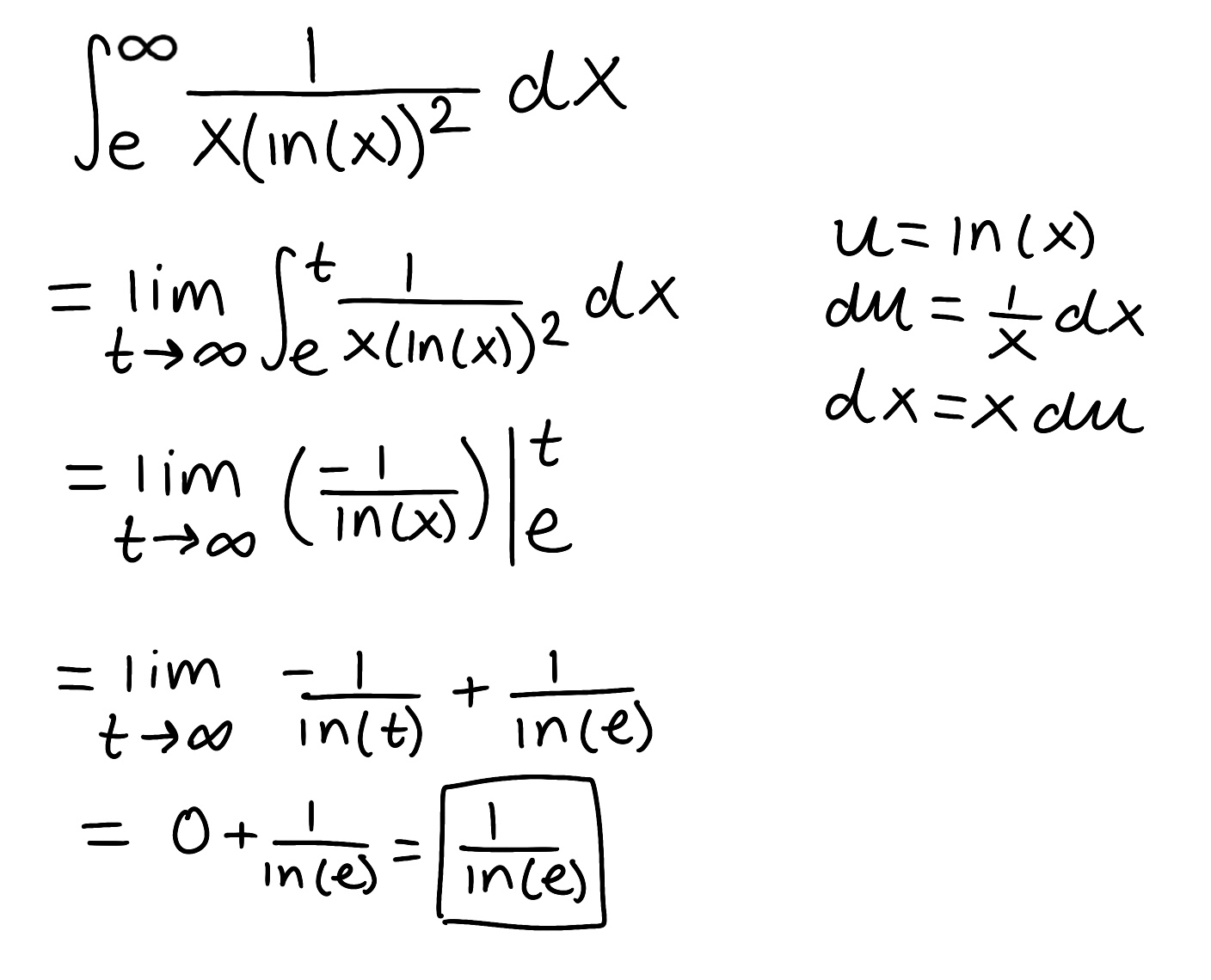
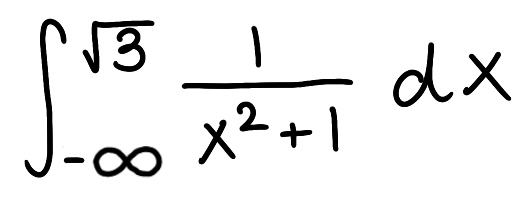
• Evaluate the integral

• Explain why the integral is improper

• Determine if the integral converges or diverges and explain why

• The integral is improper because one of the bounds is infinite

• The integral converges because the limit is finite

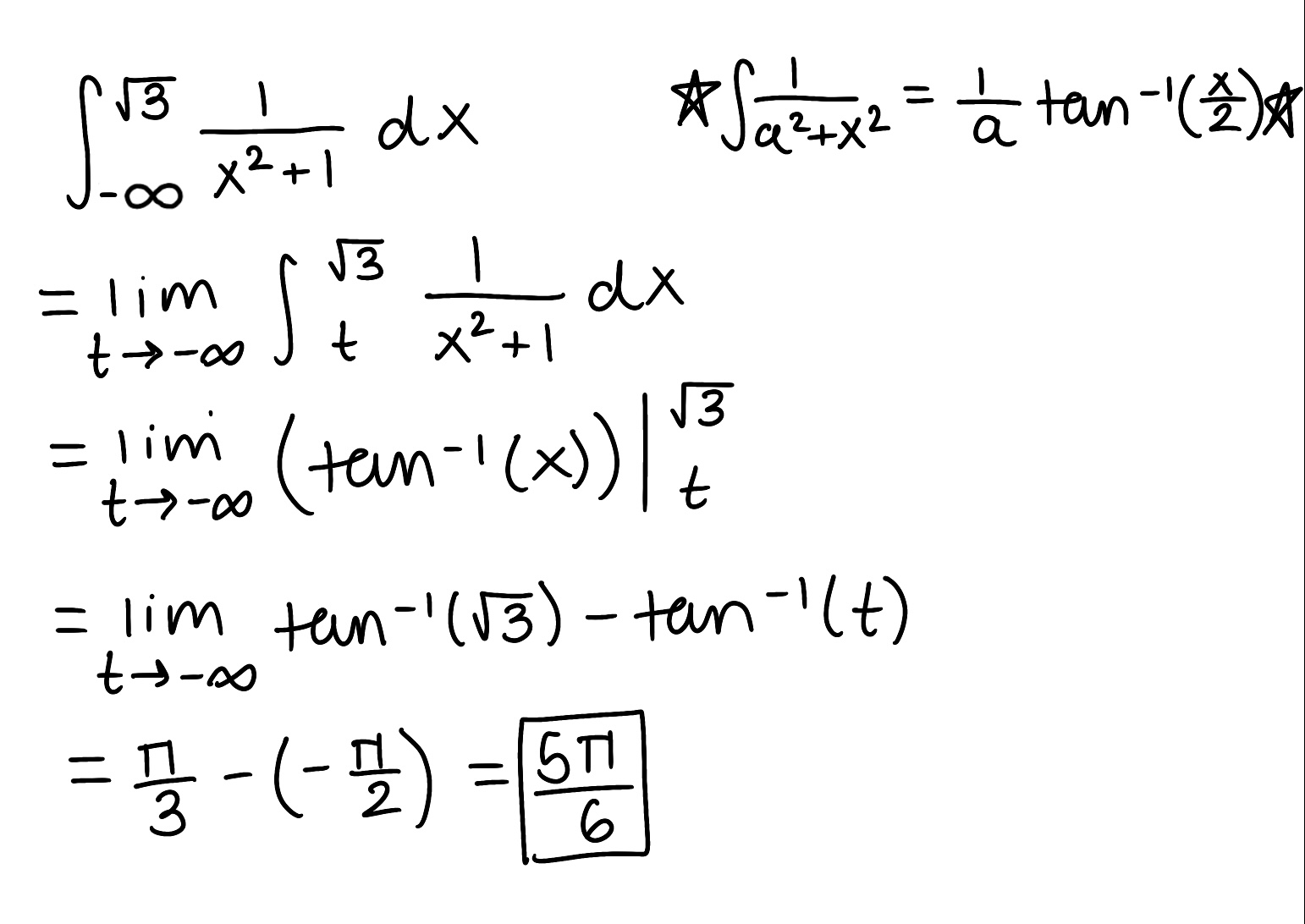
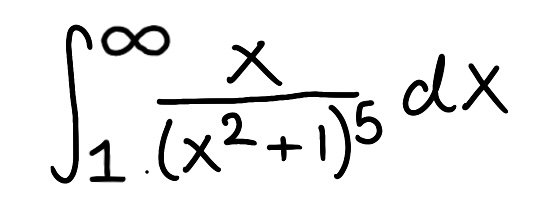
• Evaluate the integral

• Explain why the integral is improper

• Determine if the integral converges or diverges and explain why

• The integral is improper because one of the bounds is infinite

• The integral converges because the limit is finite

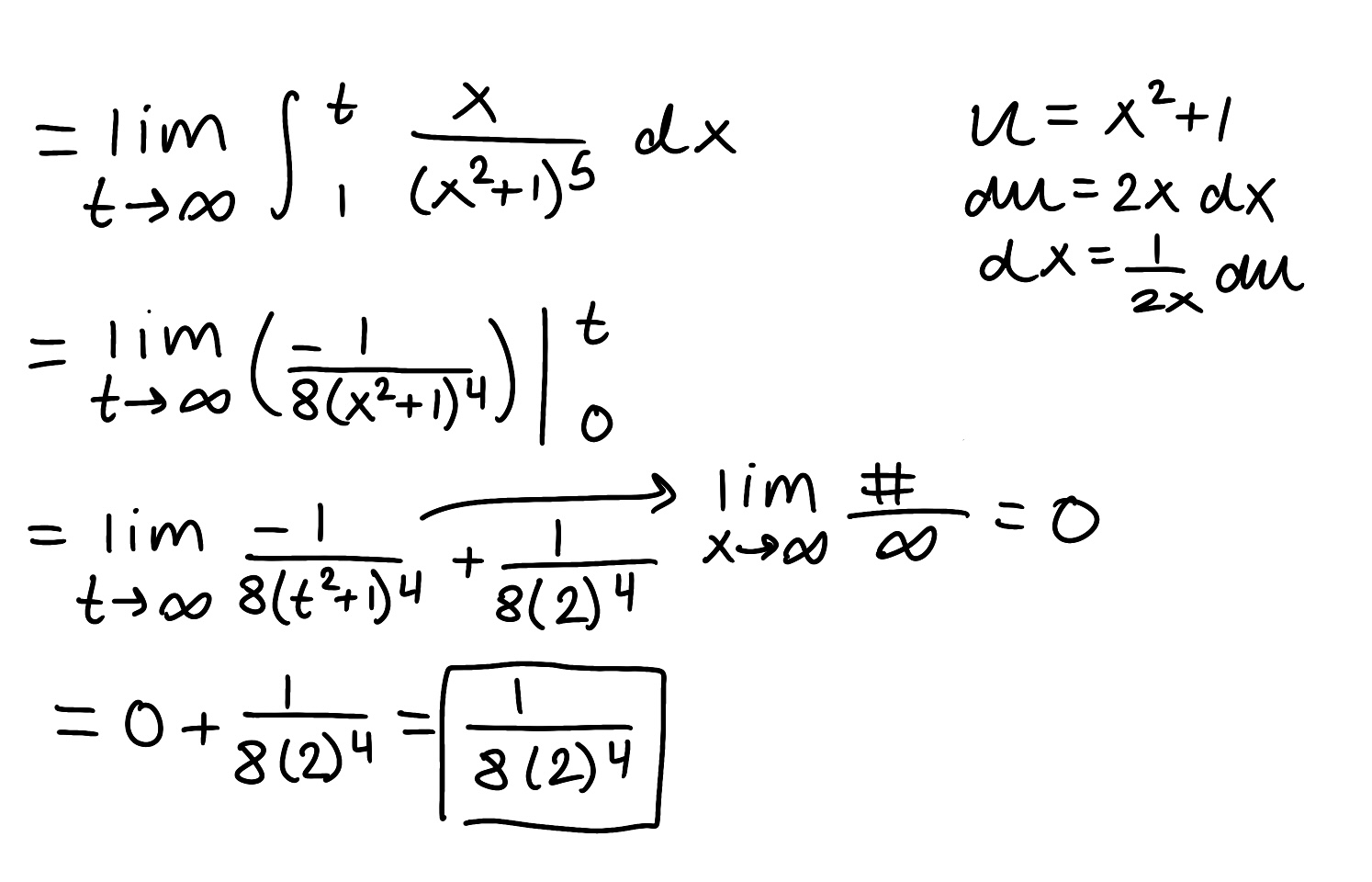
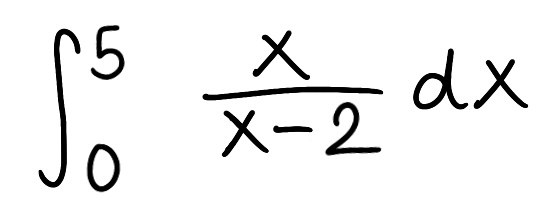
• Evaluate the integral

• Explain why the integral is improper

• Determine if the integral converges or diverges and explain why

• The integral is improper because there is a discontinuity at x=2

• The integral diverges because the limit is infinite

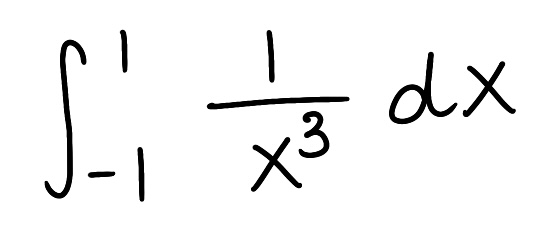
• Evaluate the integral

• Explain why the integral is improper

• Determine if the integral converges or diverges and explain why

• The integral is improper because there is a discontinuity at x=0

• The integral diverges because the limit is infinite

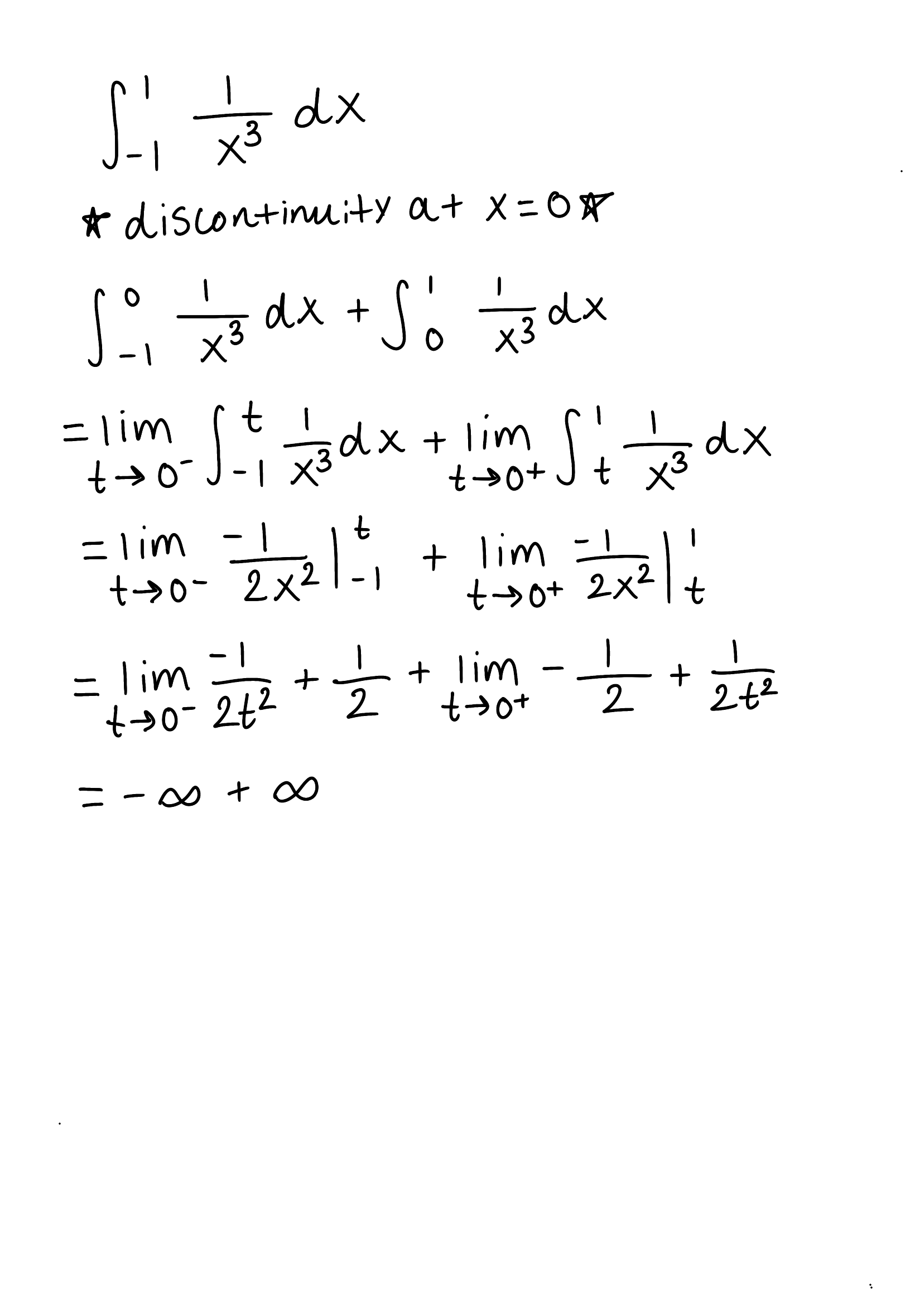
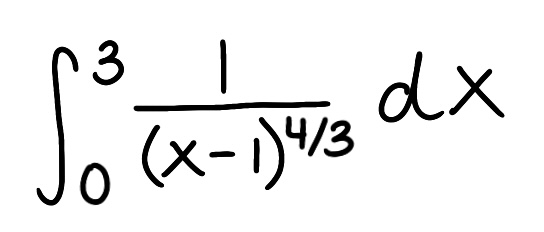
• Evaluate the integral

• Explain why the integral is improper

• Determine if the integral converges or diverges and explain why

• The integral is improper because there is a discontinuity at x=1

• The integral diverges because the limit is infinite

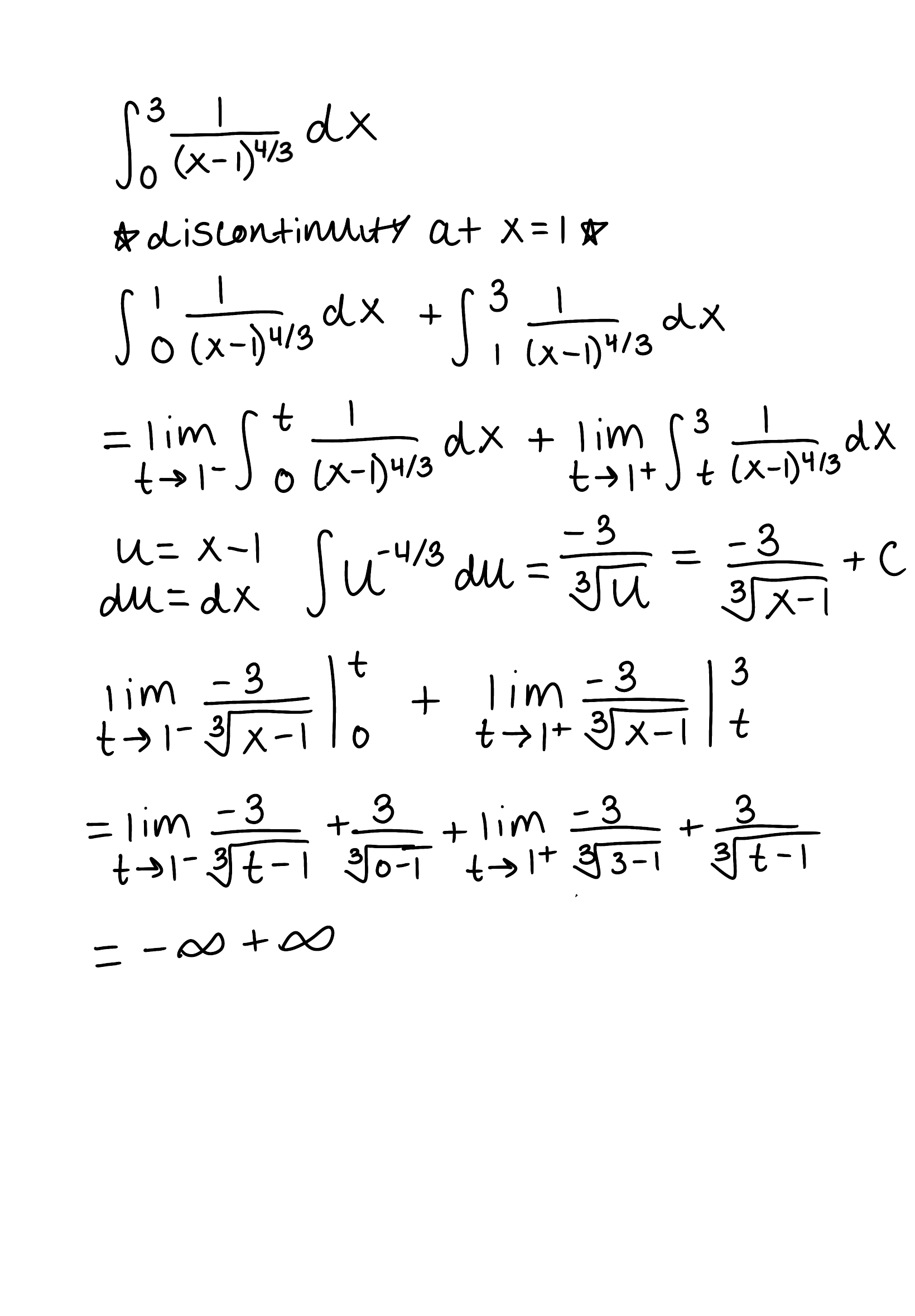
*remember that when when you have to split apart the integral because there is a discontinutiy that is inbetween the bounds, the answer will always be divergent

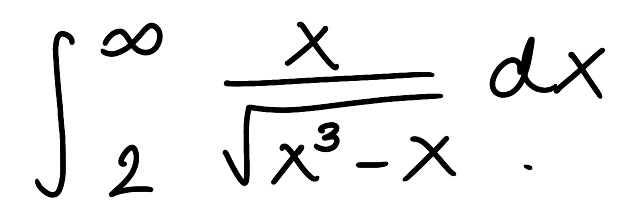
Use the Comparison Theorem to determine if the improper integral converges or diverges (do not evaluate the integral)

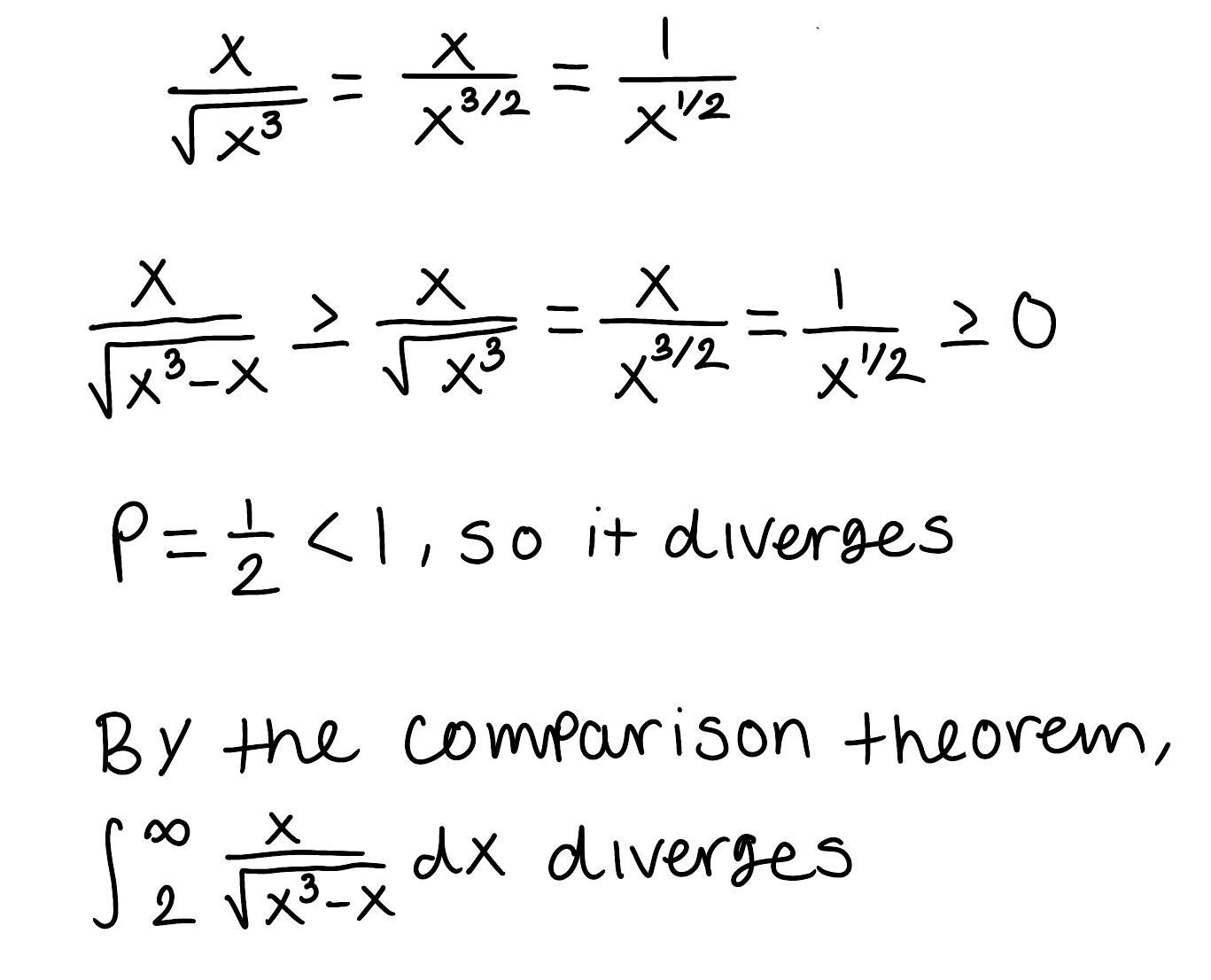
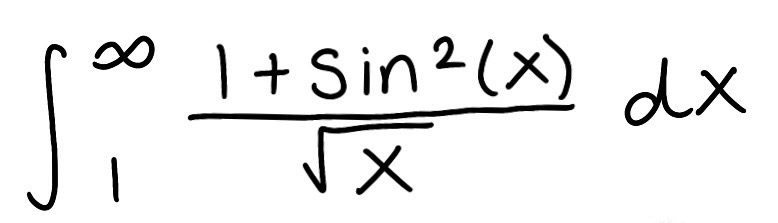
Use the Comparison Theorem to determine if the improper integral converges or diverges (do not evaluate the integral)

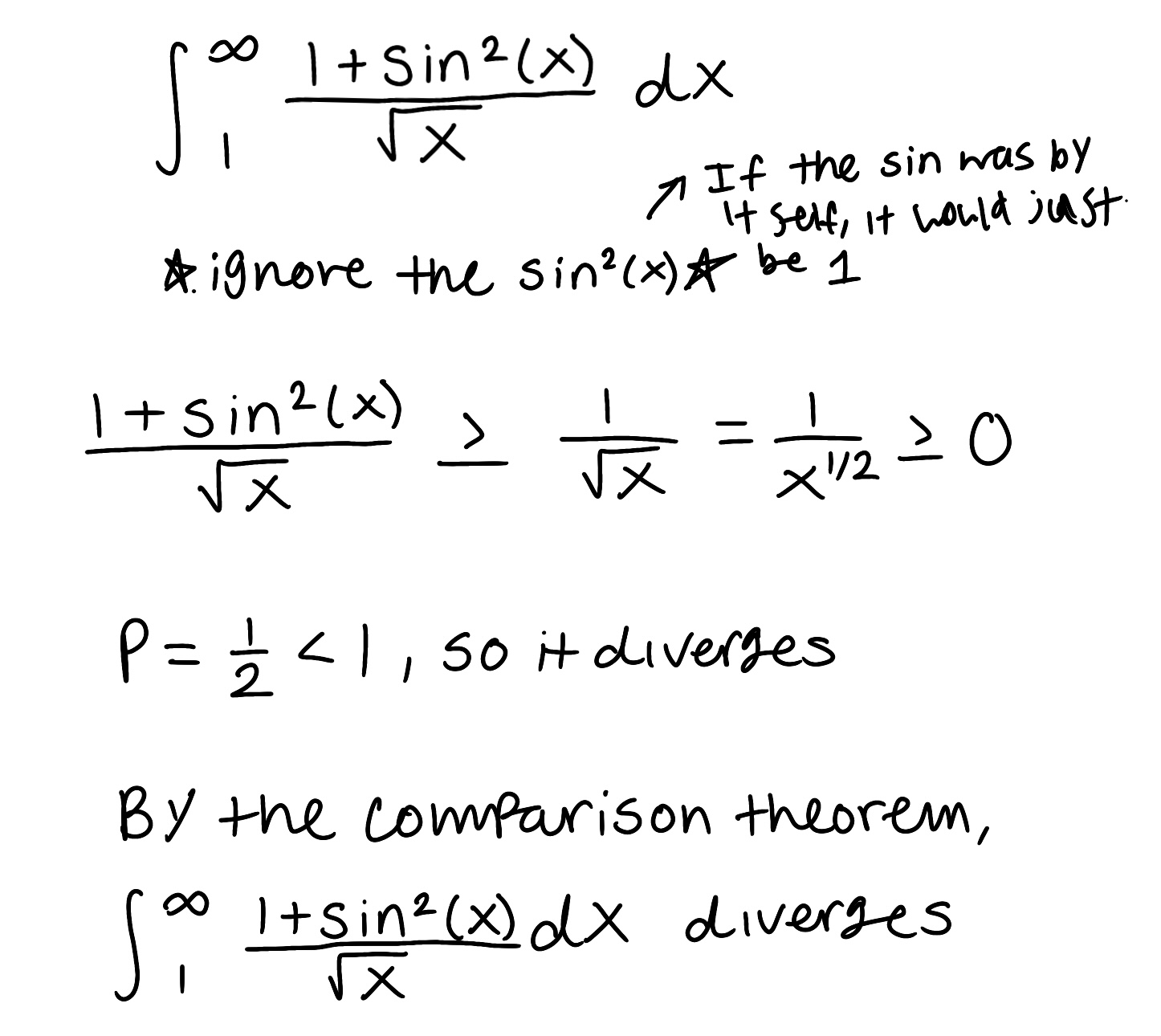
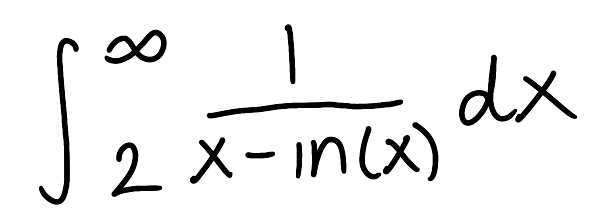
Use the Comparison Theorem to determine if the improper integral converges or diverges (do not evaluate the integral)

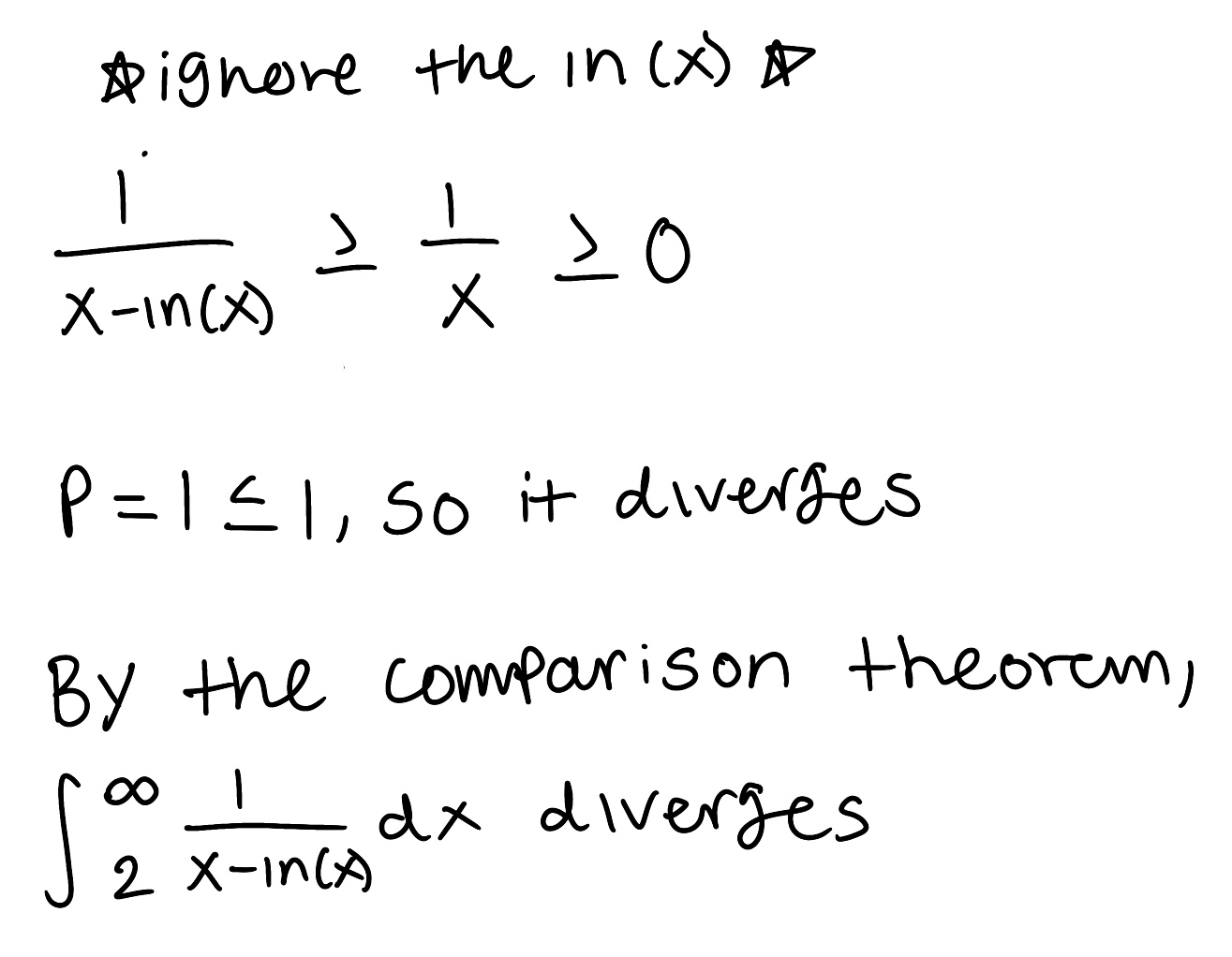
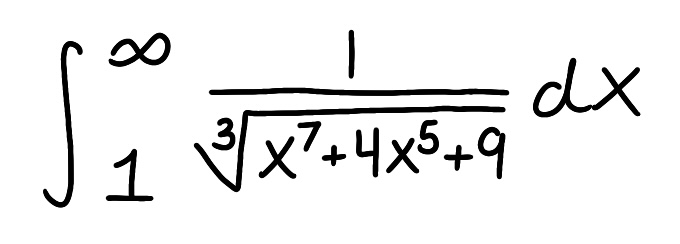
Use the Comparison Theorem to determine if the improper integral converges or diverges (do not evaluate the integral)

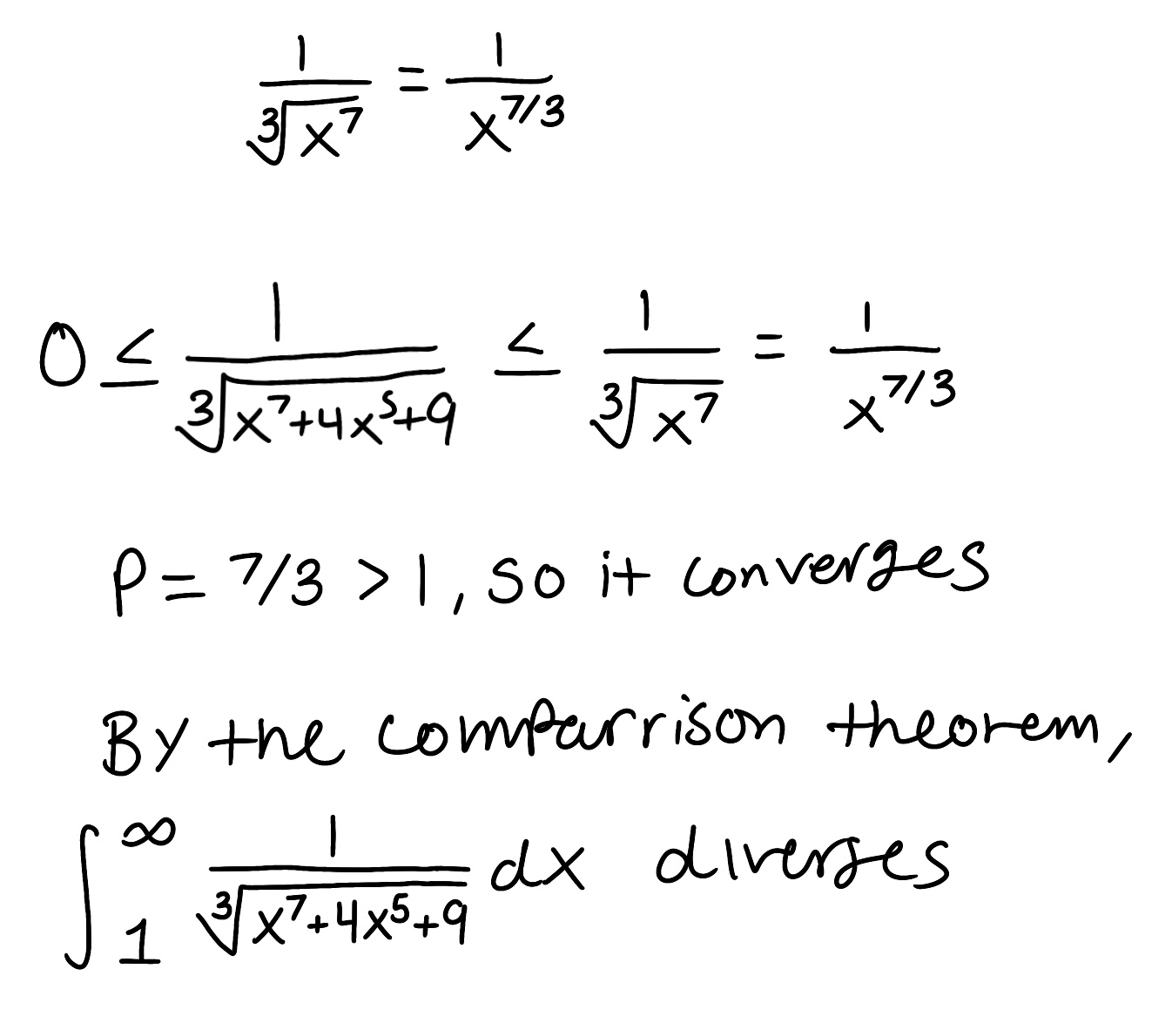
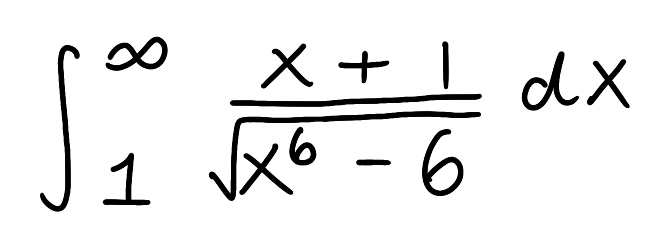
Use the Comparison Theorem to determine if the improper integral converges or diverges (do not evaluate the integral)

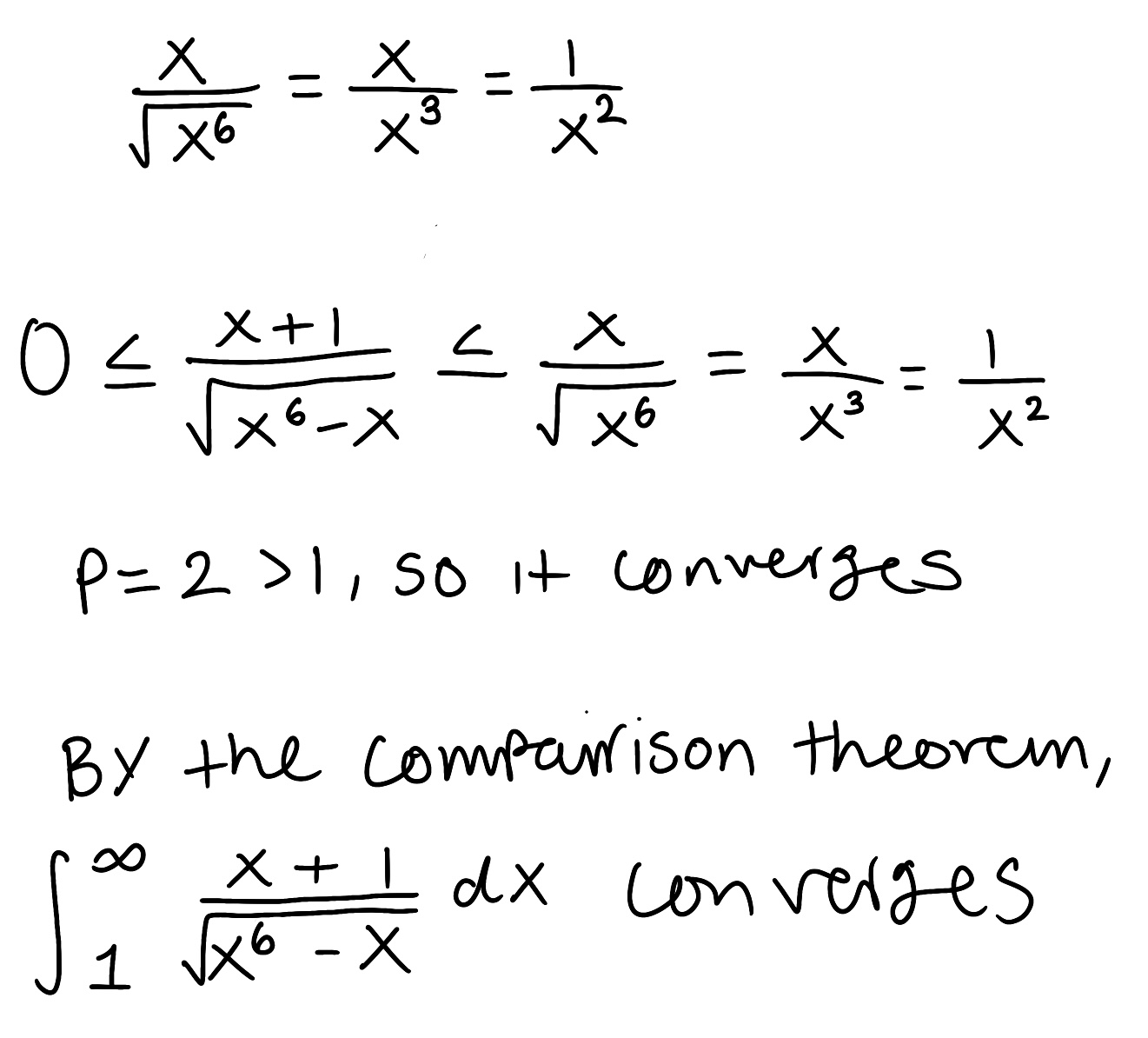
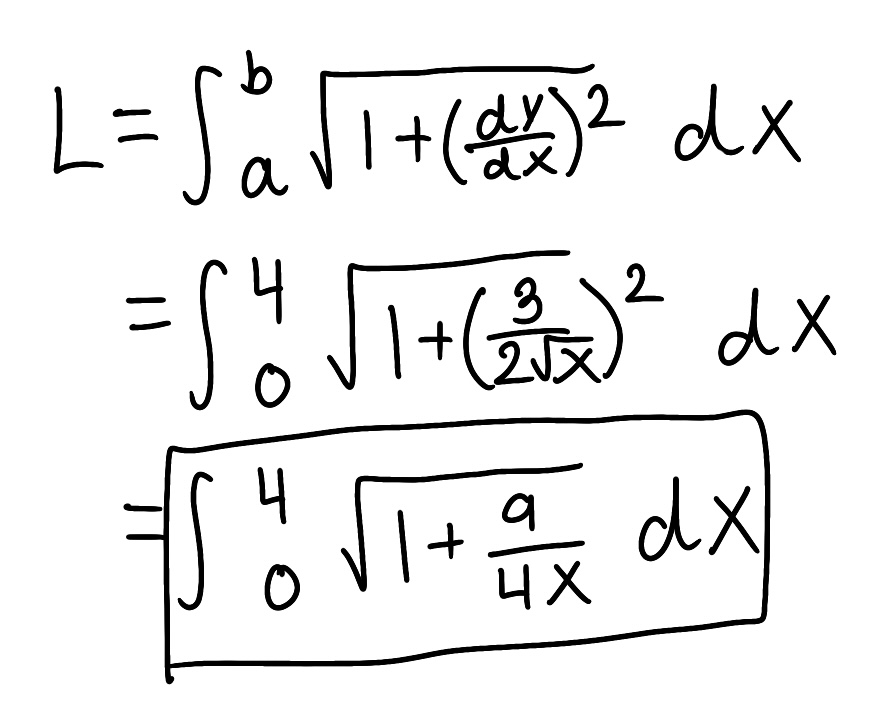
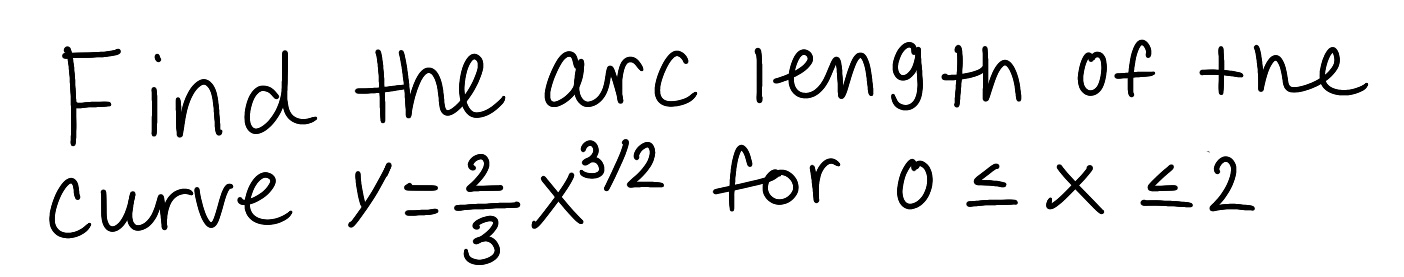
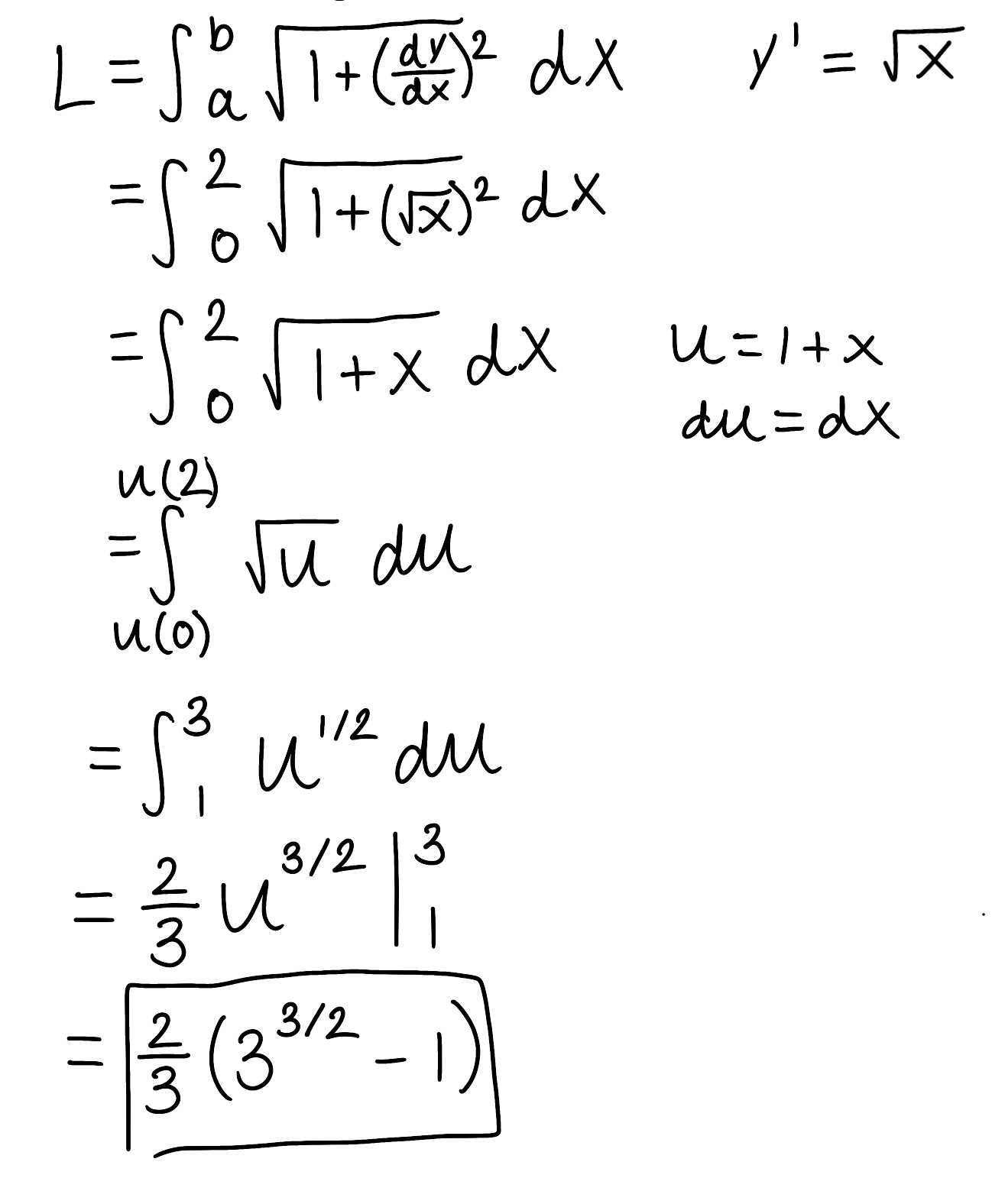
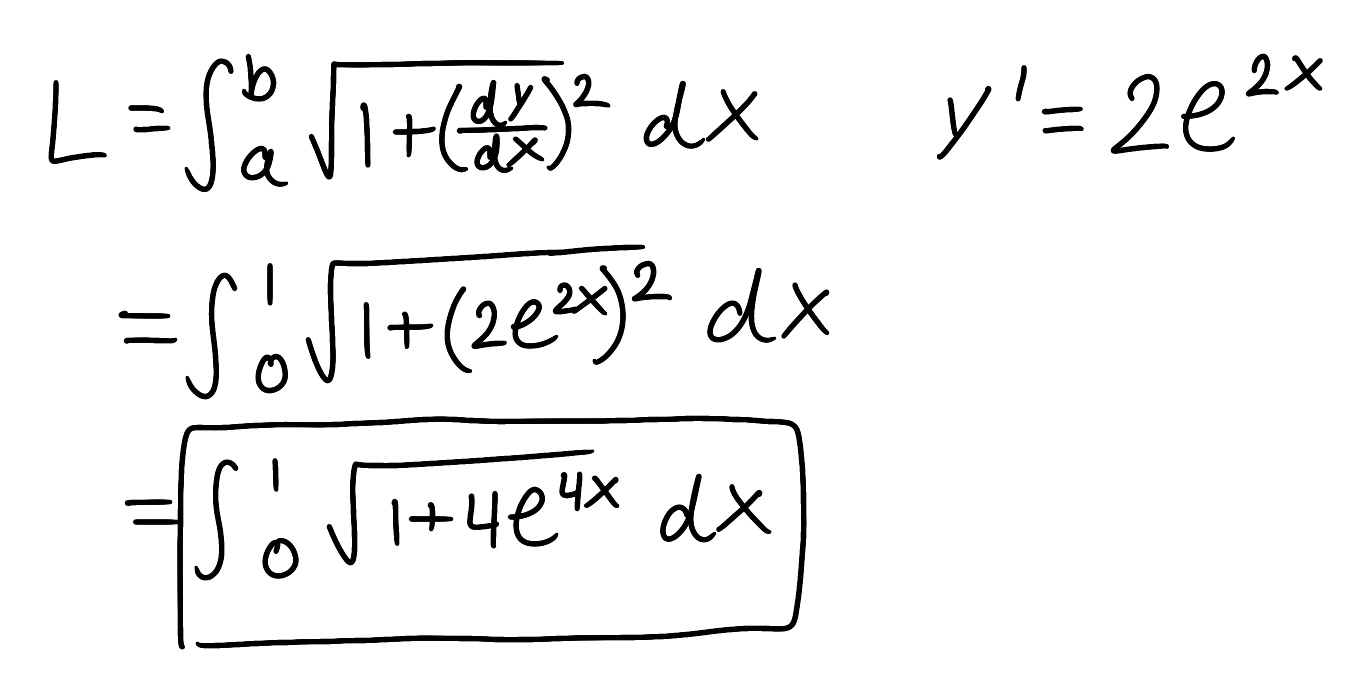
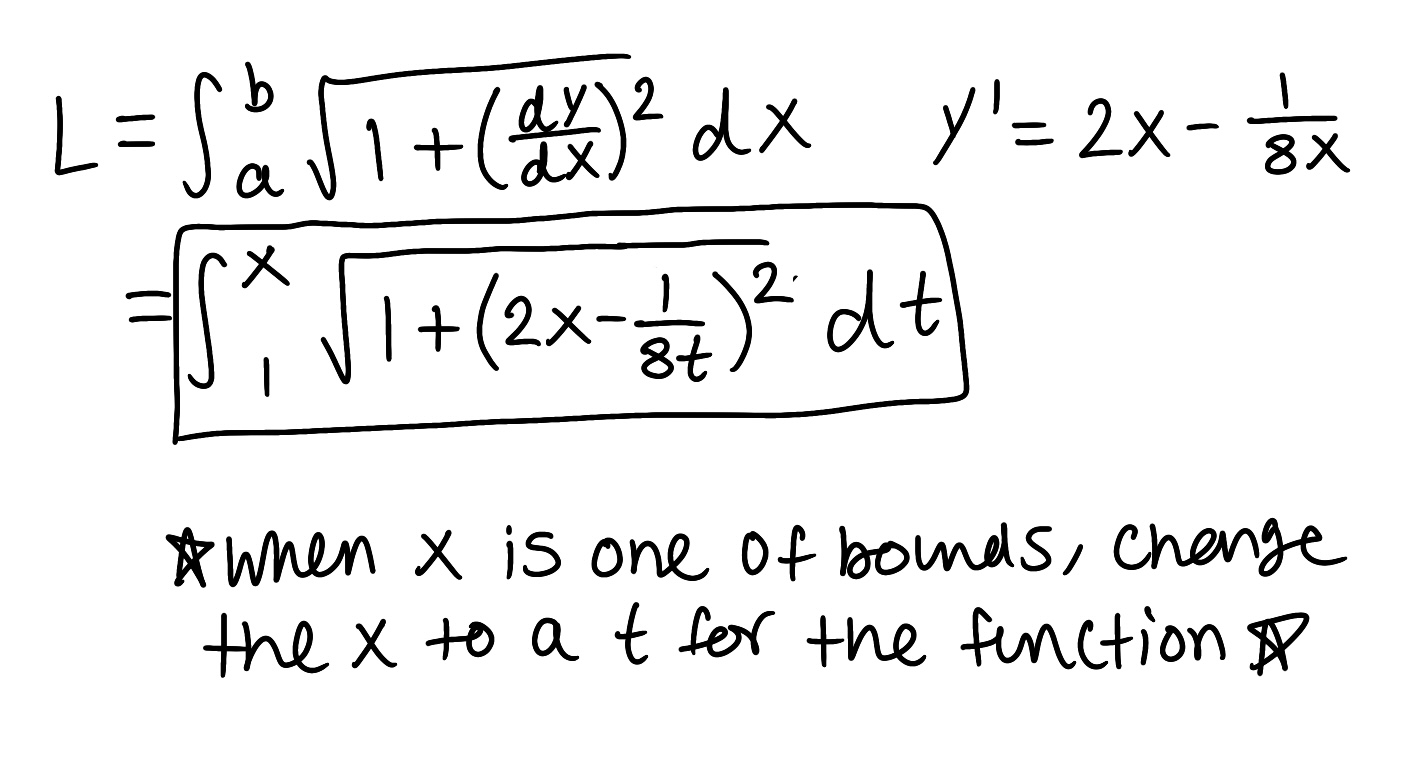
Decompose the rational function into partial fractions

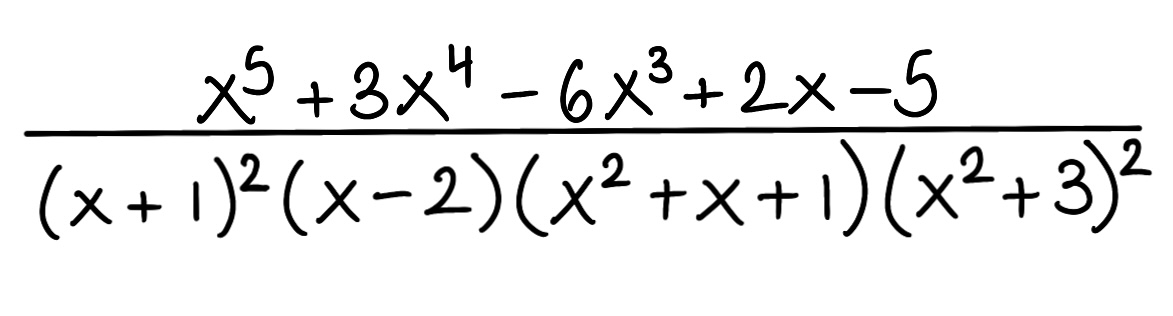
Evaluate the integral

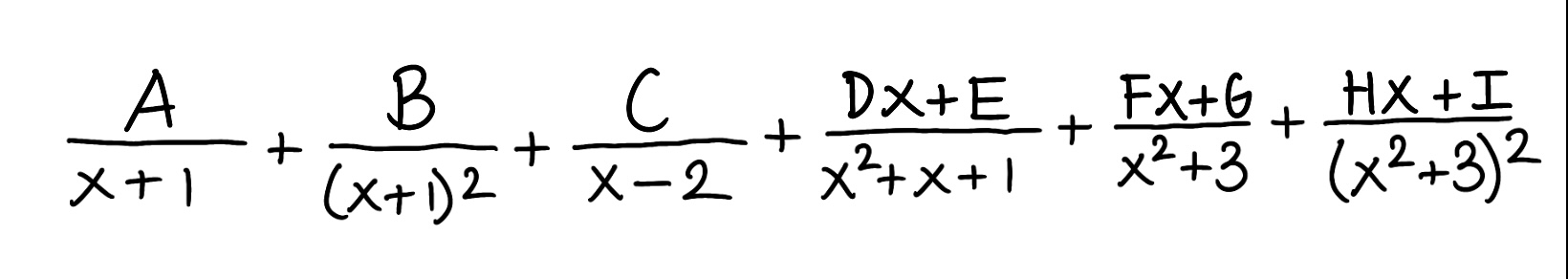
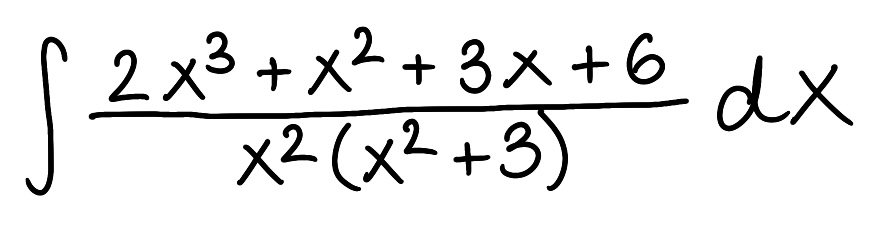
Evaluate the integral

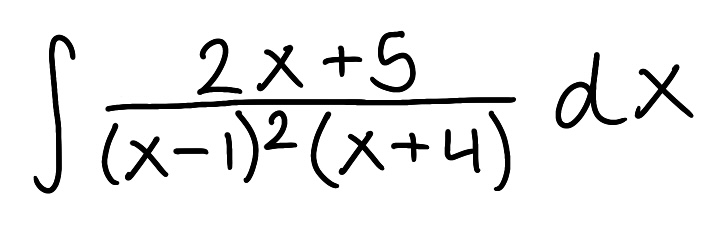
Evaluate the integral

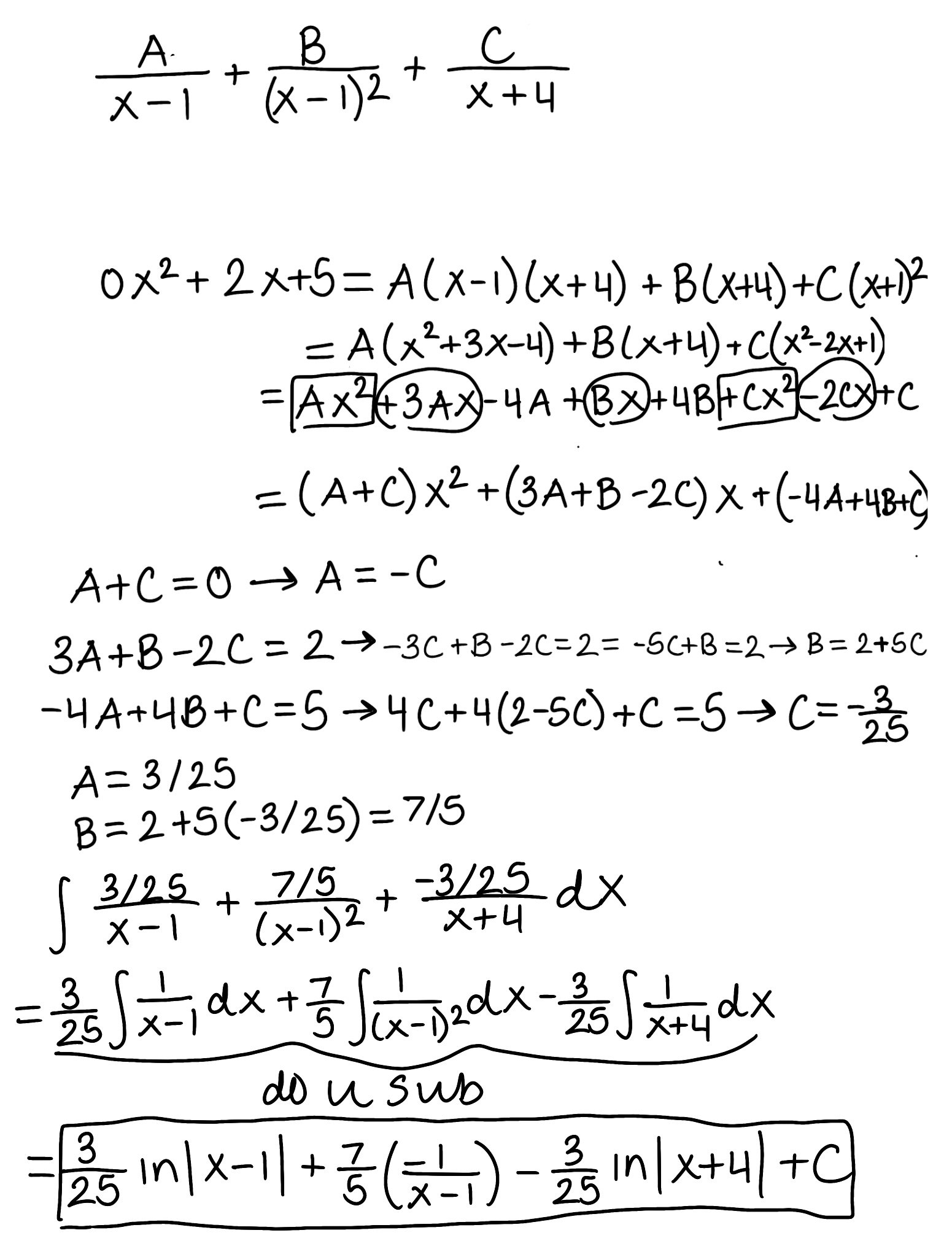
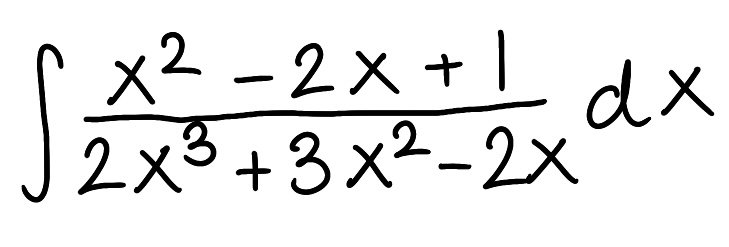
Evaluate the integral

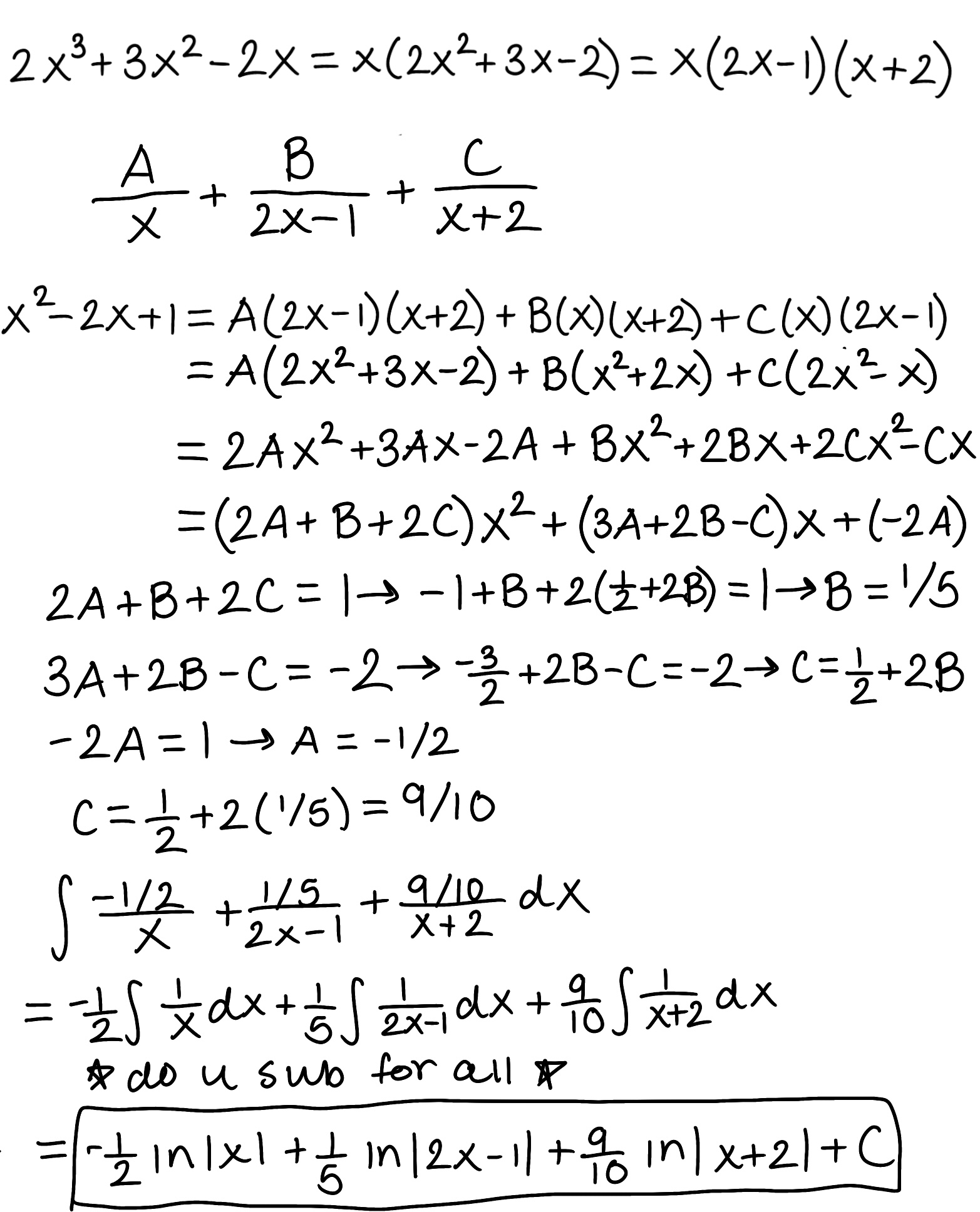
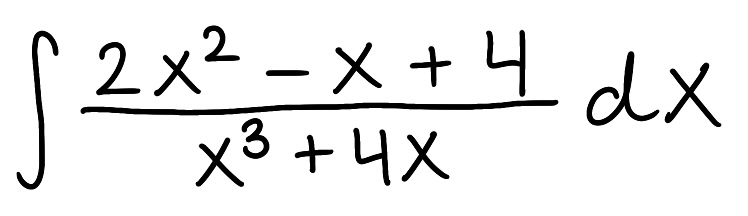
Evaluate the integral

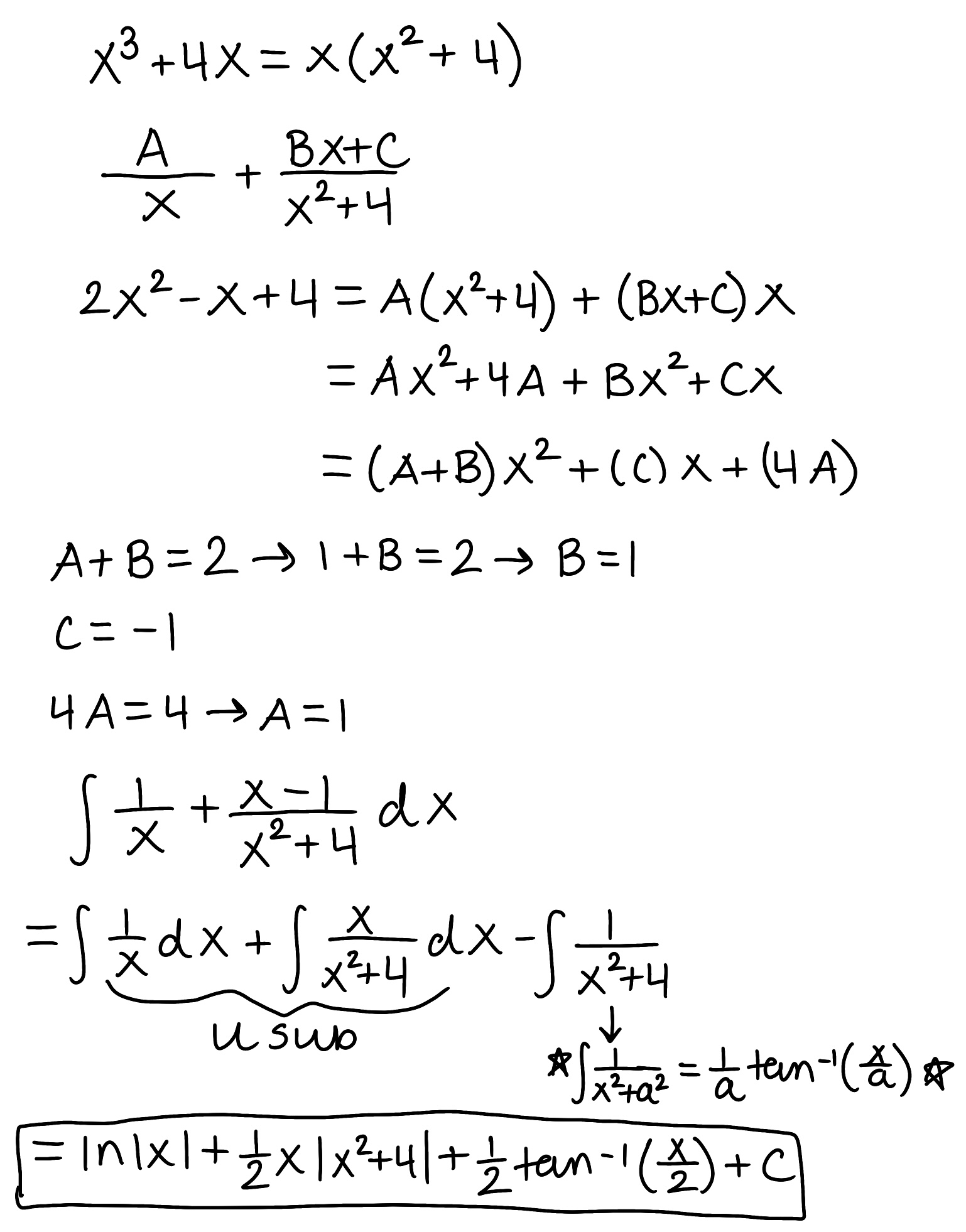
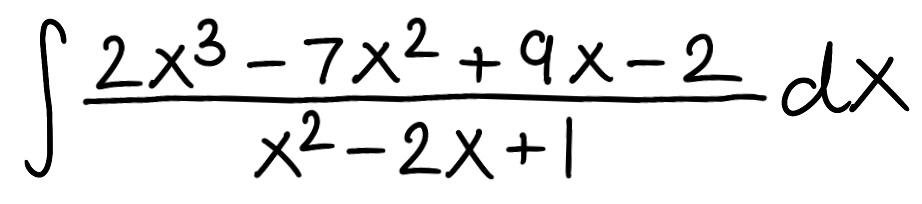
Evaluate the integral

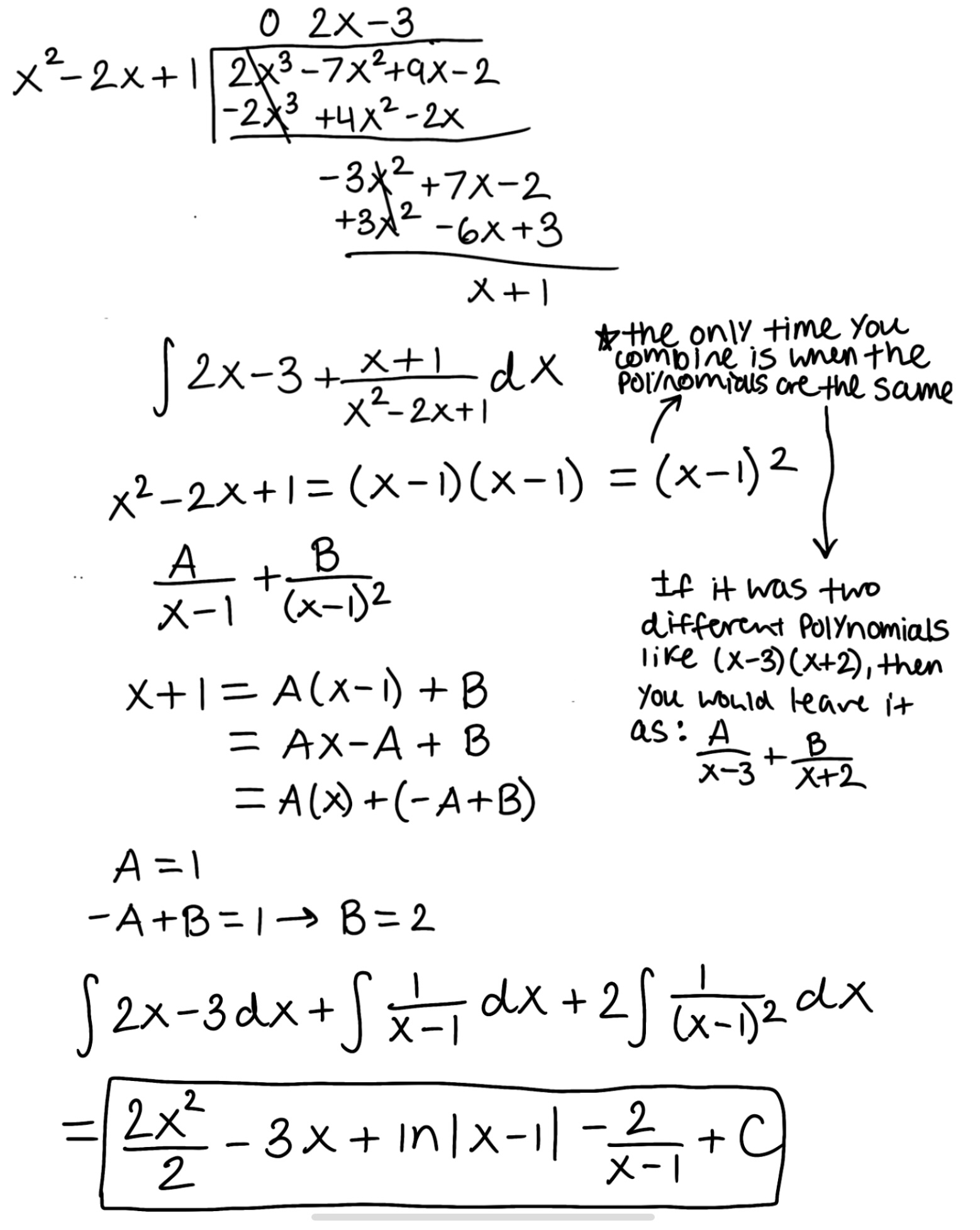
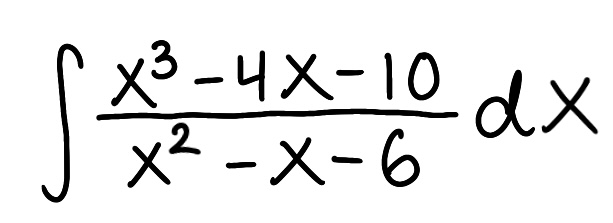
Evaluate the integral

Eliminate the parameter to find a Cartesian equation of the curve.

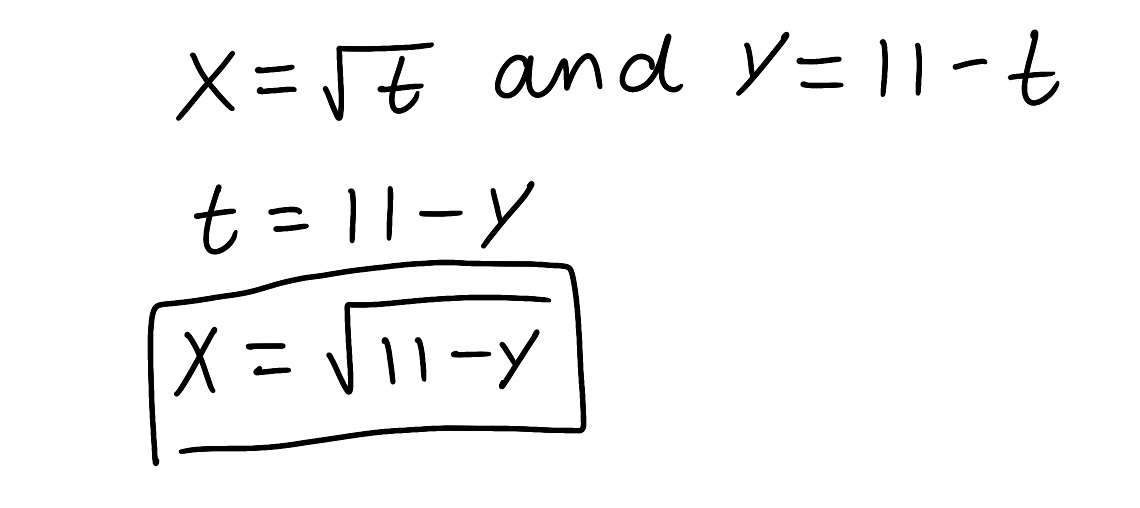
Eliminate the parameter to find a Cartesian equation of the curve.

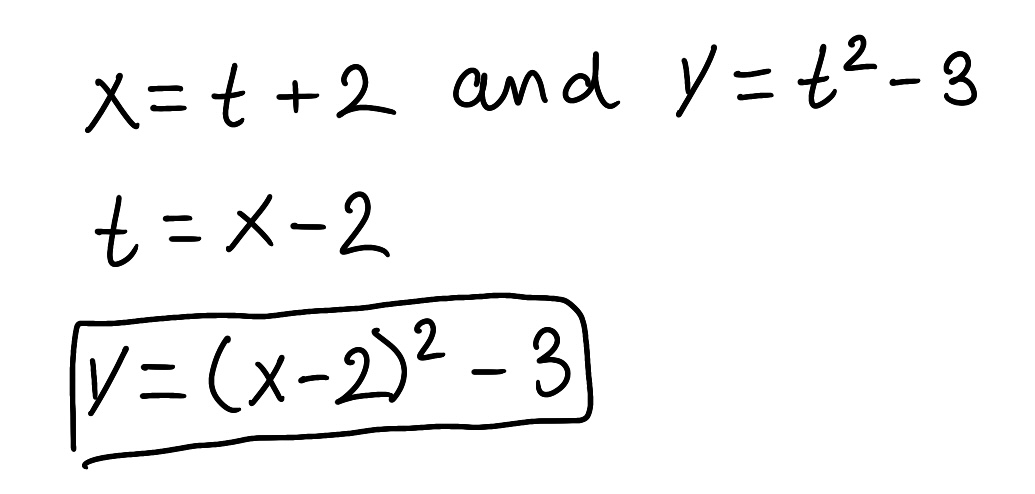
Eliminate the parameter to find a Cartesian equation of the curve.

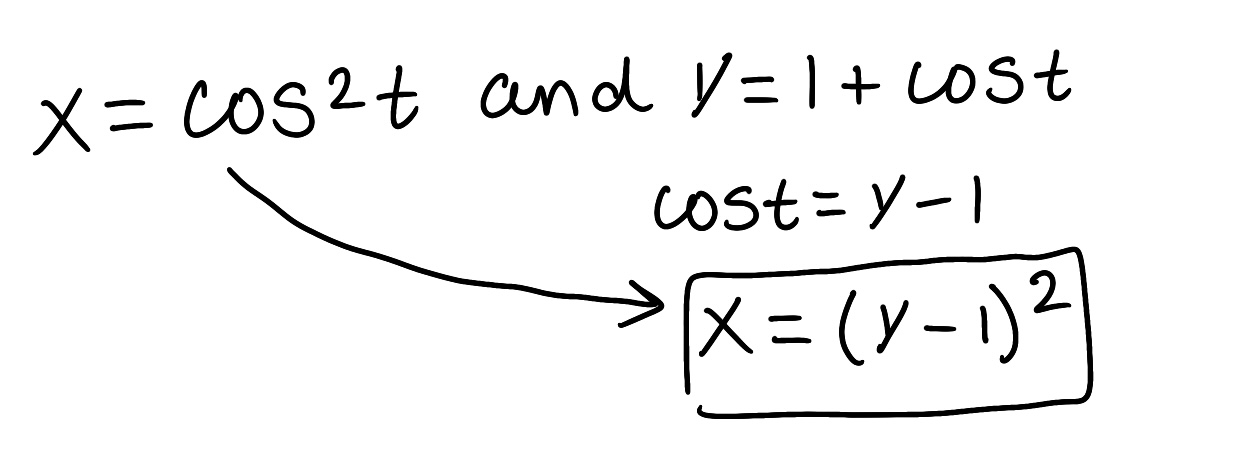
Eliminate the parameter to find a Cartesian equation of the curve.

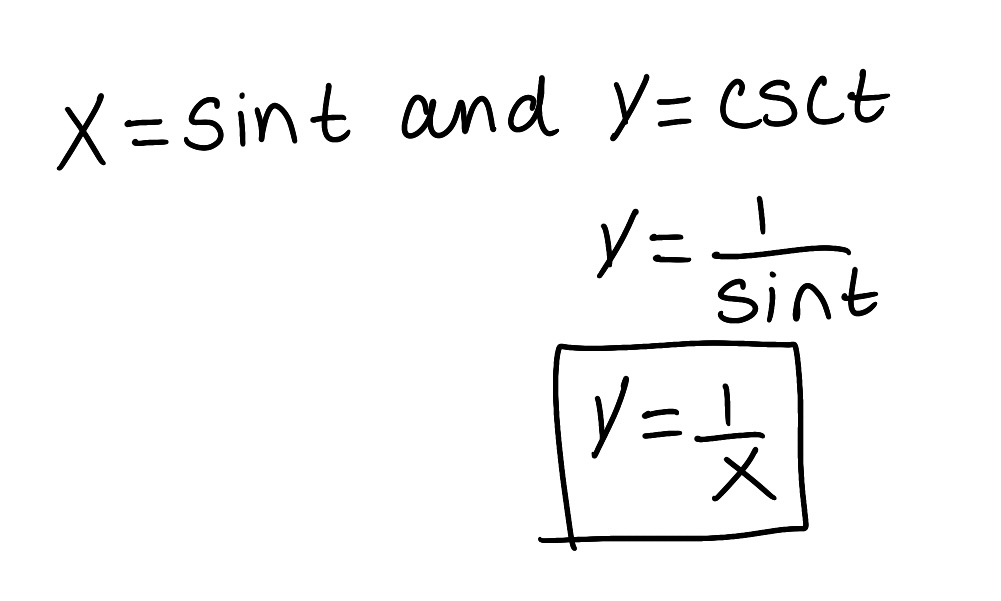
Eliminate the parameter to find a Cartesian equation of the curve.

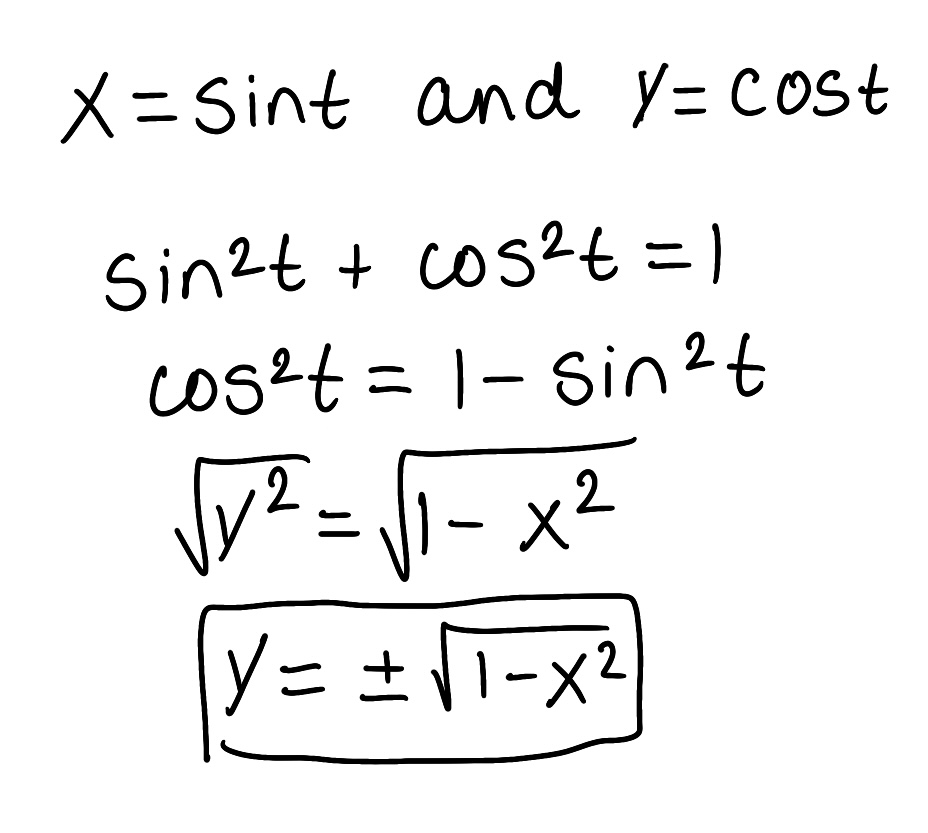
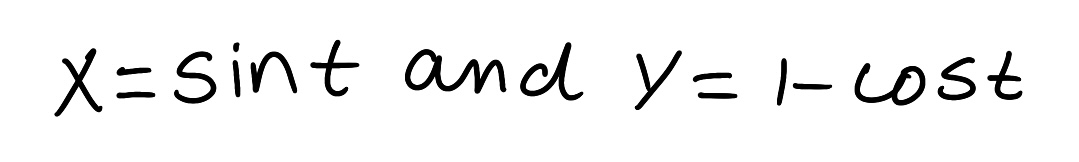
Eliminate the parameter to find a Cartesian equation of the curve.

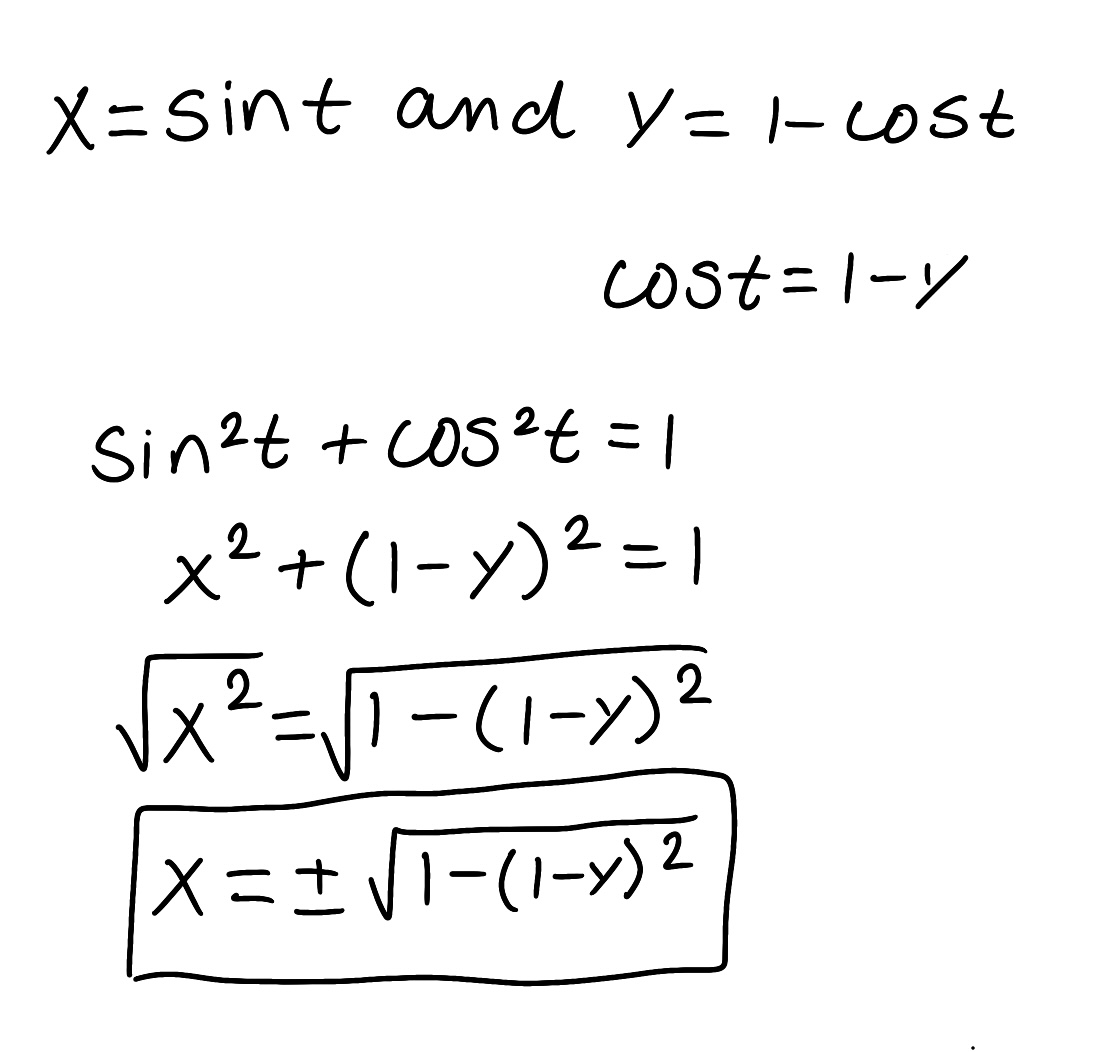
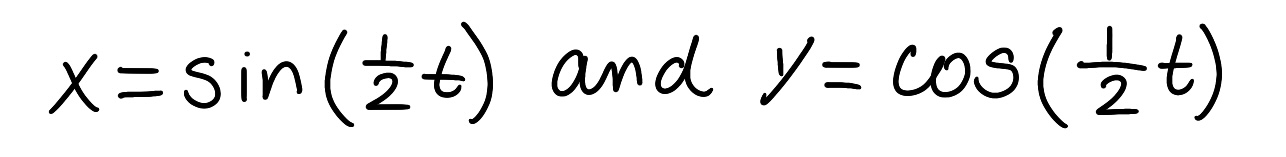
Eliminate the parameter to find a Cartesian equation of the curve.

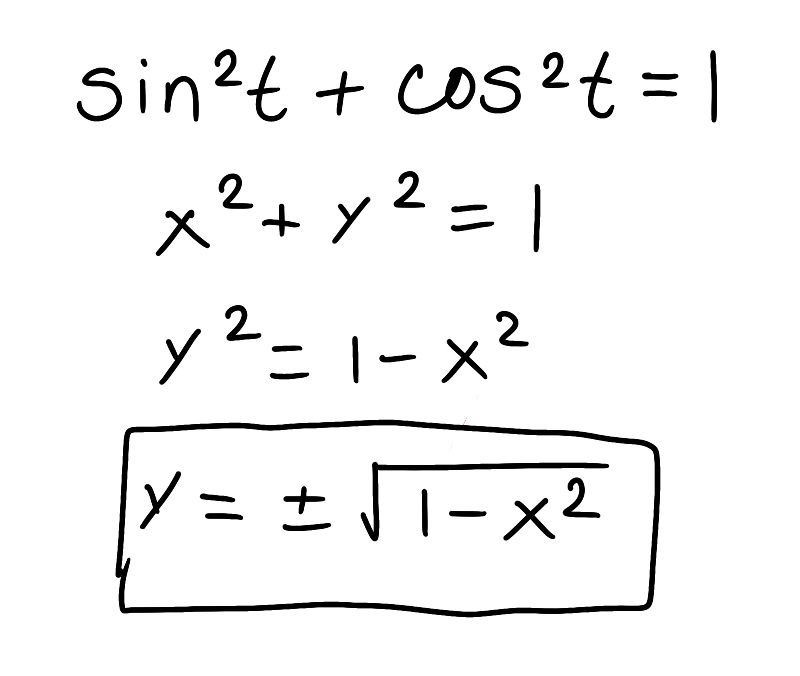
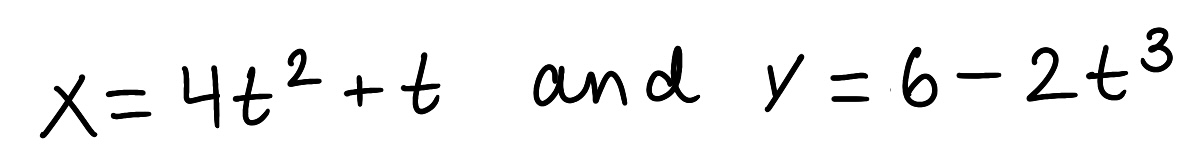
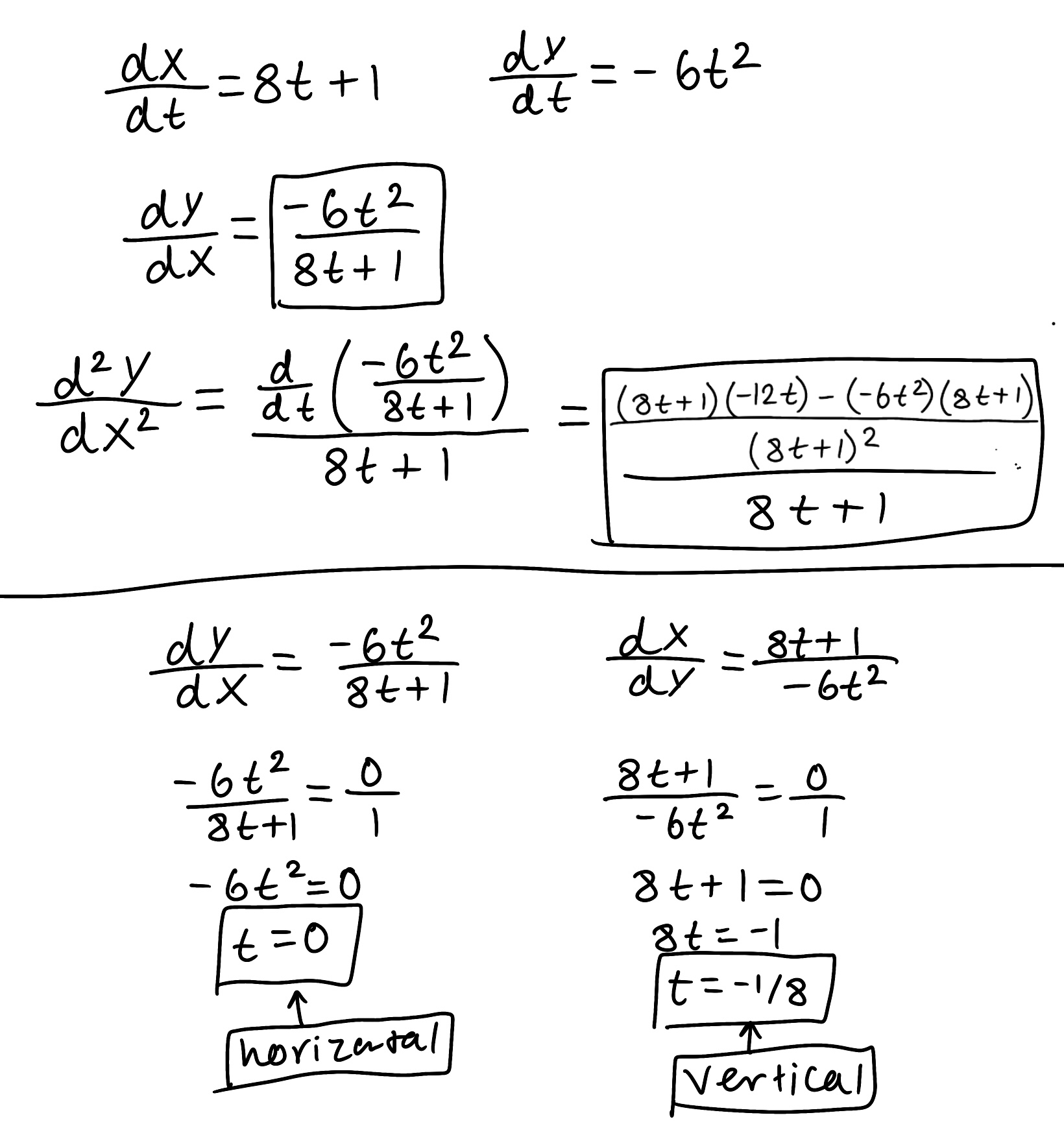
a. Find dy/dx and d²y/dx²

b. Find the values of t where the tangent is horizontal or vertical