unsupervised learning
0.0(0)
Card Sorting
1/25
There's no tags or description
Looks like no tags are added yet.
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
26 Terms
1
New cards
notation
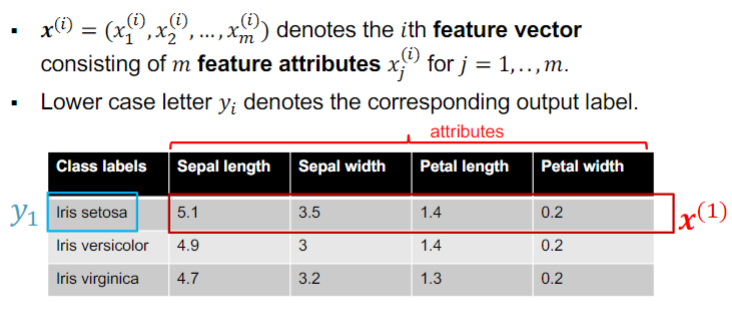
2
New cards
classification
Predict categorical labels
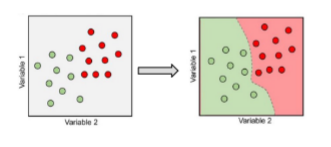
3
New cards
regression
Predict continuous-valued \n labels
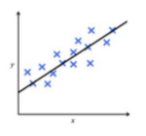
4
New cards
unsupervised vs supervised data set
unsupervised is unlabeled, supervised is labeled

5
New cards
applications of clustering
* google news
* market segmentation
* social network analysis
* market segmentation
* social network analysis
6
New cards
clusters
Find natural groupings among observations and segment observations into clusters/groups such that objects within a cluster have high similarity (high intra cluster similarity) and objects across clusters have low similarity (low intra cluster similarity)
7
New cards
clustering algorithms
automatically find ‘classes’
8
New cards
challenges of unsupervised learning
* no simple goal
* validation of results is subjective
* often used more in exploratory data analysis
* validation of results is subjective
* often used more in exploratory data analysis
9
New cards
why use unsupervised learning
* labeled data is expensive and difficult to collect, whereas unlabeled data is cheap and abundant
* compressed representation saves on storage and computation
* reduce noise and irrelevant attributes in high dimensional data
* pre-processing step for supervised learning
* compressed representation saves on storage and computation
* reduce noise and irrelevant attributes in high dimensional data
* pre-processing step for supervised learning
10
New cards
clustering is
unsupervised classification
11
New cards
distance functions
Measures the strength of relationship between any two feature vectors

12
New cards
properties of distance functions
* Distance between two points is always non-negative
* Distance between a point to itself is zero
* Distance is symmetric
* Distance satisfies a triangle inequality
* Distance between a point to itself is zero
* Distance is symmetric
* Distance satisfies a triangle inequality
13
New cards
distance function takeaways
* Different choice of distance functions yields different measures of similarity
* Distance functions implicitly assign more weighting to features with large anges than to those with small ranges
* Rule of thumb: when no a priori domain knowledge is available, clustering should follow the principle of equal weightings to each attribute \[Mirkin, 2005\]
* This necessitates need for normalization/data pre-processing/feature scaling of feature vectors.
* Distance functions implicitly assign more weighting to features with large anges than to those with small ranges
* Rule of thumb: when no a priori domain knowledge is available, clustering should follow the principle of equal weightings to each attribute \[Mirkin, 2005\]
* This necessitates need for normalization/data pre-processing/feature scaling of feature vectors.
14
New cards
normalisation of feature vectors
attributes contribute approximately equally to the similarity measure
15
New cards
min-max normalisation
* all feature attributes rescaled to lie in the range \[0,1\]
* sensitive to outliers
* sensitive to outliers
![* all feature attributes rescaled to lie in the range \[0,1\]
* sensitive to outliers](https://knowt-user-attachments.s3.amazonaws.com/dec92b87ef7b4ee3b328568db1eeab79.jpeg)
16
New cards
Z-score standardization
* all feature attributes have mean 0 and standard deviation 1
* not bounded range
* not bounded range
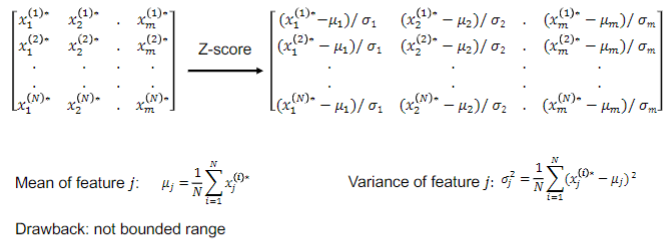
17
New cards
distance matrix

18
New cards
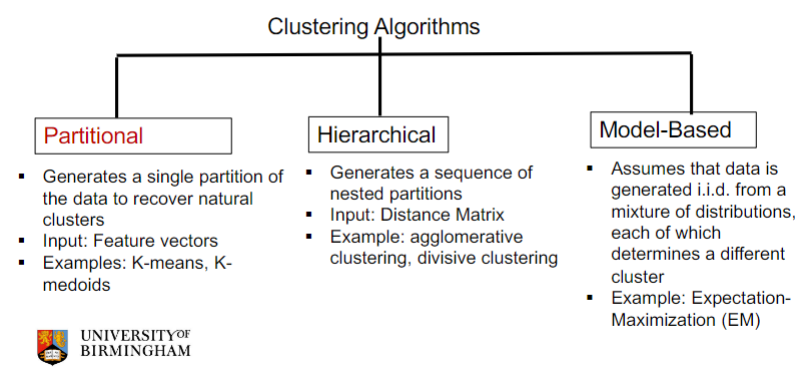
types of clustering algorithms
* partitional
* hierarchical
* model-based
* hierarchical
* model-based
19
New cards
partitional clustering algorithm
* Generates a single partition of the data to recover natural clusters
* Input: Feature vectors
* Examples: K-means, K-medoids
* Input: Feature vectors
* Examples: K-means, K-medoids

20
New cards
Hierarchical
* Generates a sequence of nested partitions
* Input: Distance Matrix
* Example: agglomerative clustering, divisive clustering
* Input: Distance Matrix
* Example: agglomerative clustering, divisive clustering
21
New cards
Model-Based
* Assumes that data is generated i.i.d. from a mixture of distributions, each of which determines a different cluster
* Example: Expectation-Maximization (EM)
* Example: Expectation-Maximization (EM)
22
New cards
measure of intra-cluster similarity
* Commonly used distance measure: squared Euclidean distance
* Centroid of a cluster is usually taken as the average of all examples in the cluster
* Variability determines how compact the cluster is
* Centroid of a cluster is usually taken as the average of all examples in the cluster
* Variability determines how compact the cluster is
23
New cards
Dissimilarity within a clustering structure 𝑪
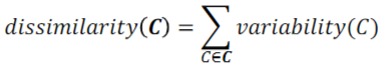
24
New cards
optimisation problem
* Find a clustering structure 𝑪 of K clusters that minimizes the following objective (see image)
* Larger clusters with high variability are penalized more than smaller clusters with high variability
* Under squared Euclidean distance, minimizing 𝑑𝑖𝑠𝑠𝑖𝑚𝑖𝑙𝑎𝑟𝑖𝑡𝑦 𝑪 is equivalent to maximizing overall inter-cluster dissimilarity (will see this in detail later).
* Larger clusters with high variability are penalized more than smaller clusters with high variability
* Under squared Euclidean distance, minimizing 𝑑𝑖𝑠𝑠𝑖𝑚𝑖𝑙𝑎𝑟𝑖𝑡𝑦 𝑪 is equivalent to maximizing overall inter-cluster dissimilarity (will see this in detail later).
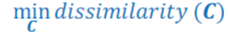
25
New cards
finding the exact solution of the dissimilarity problem is
prohibitively hard and infeasible when large number of examples present
26
New cards
iterative greedy algorithms
* Provide a sub-optimal approximate solution
* includes K-means, K-medoids
* includes K-means, K-medoids