Chapter 2 (2.1-2.3)

What is a Limit?

The value that a function approaches as the input approaches a specified point

• As x is approaching the value of “c” what is the y (output) value?

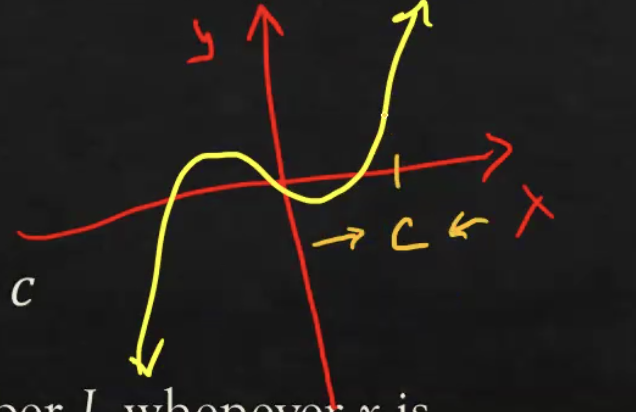
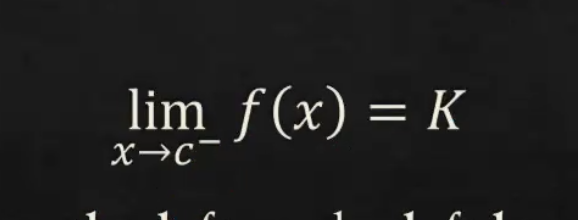
What is this Limit called?

What is the left-hand limit? “→” From negative infinity to value

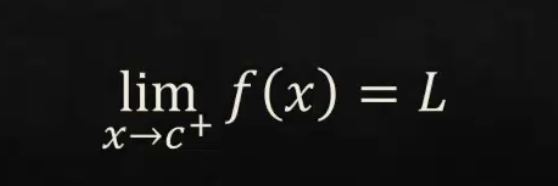
What is this Limit called?

What is the right-hand limit? “←” From positive infinity to value

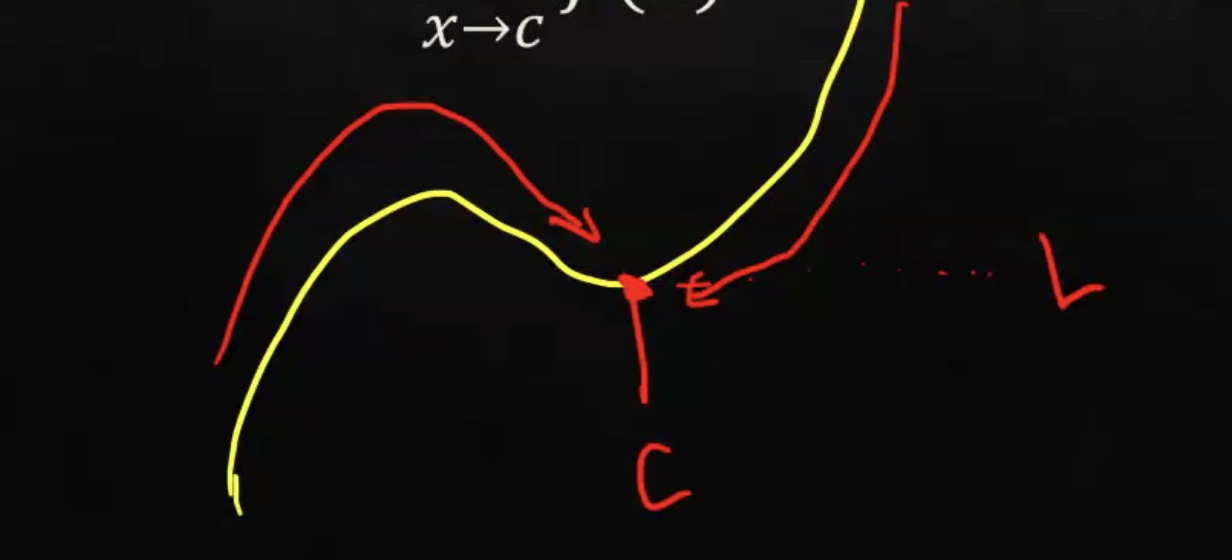
What is this called?

A Two-Sided Limit

What is a Two-Sided Limit?

When both limits from the right and left are equal.

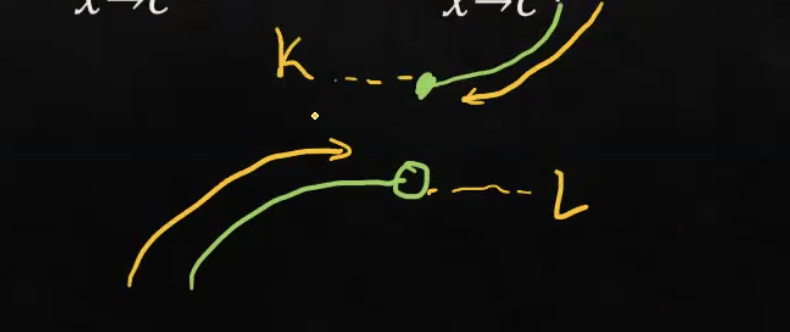
Is this a two-sided limit?

No both sides are at a different value.

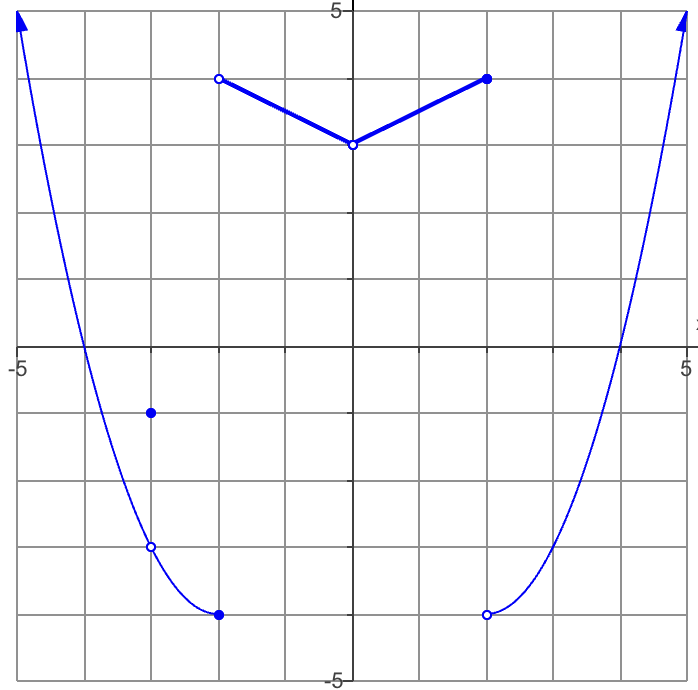
Find the limit of x→-2^+

• Approaching from the right (look for positive numbers). cause it’s positive)

• The answer: 4

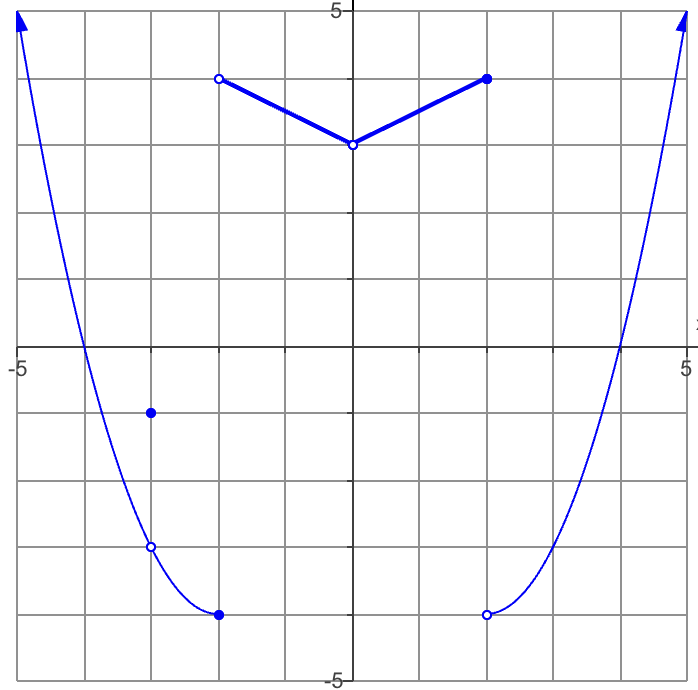
Find the limit of x→-2^-

• Approaching from the left (look for negative values)

• Answer: -4

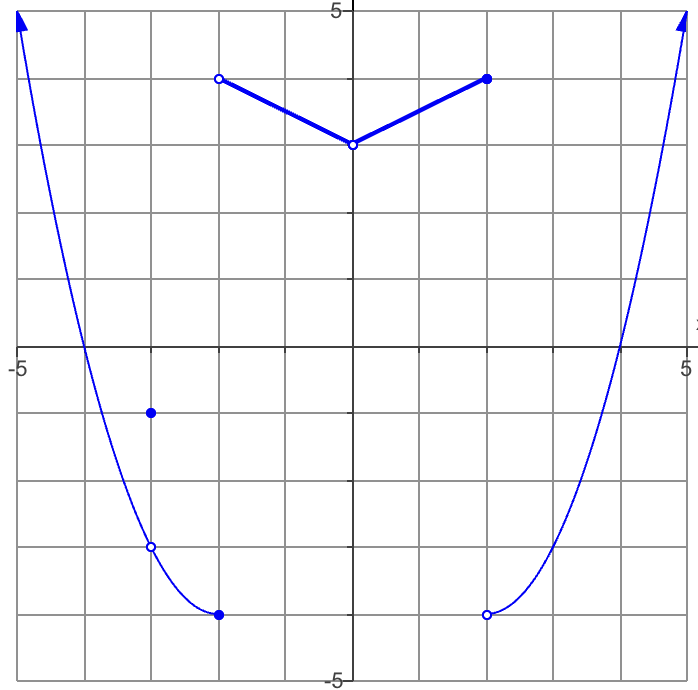
Find the limit of x→-2

Since it has no positive or negative sign attached, this is asking for the Two-Sided Limit.

• Since they are different values, no two-sided limit

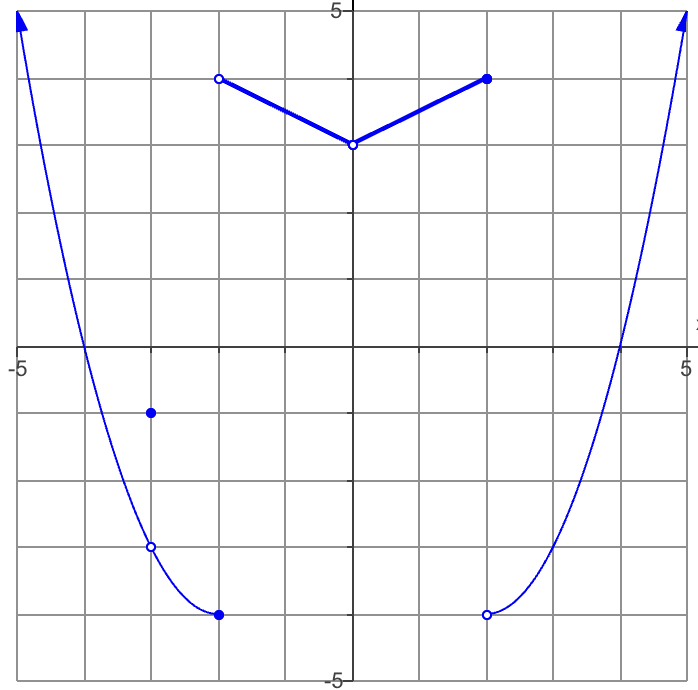
Find the function value f(-2)

! look for the closed circle!

= -4

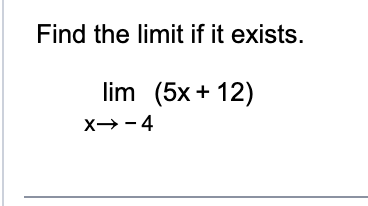
Evaluate the expression

• Move the 5 over

5Lim x (x→-4) + Lim12 (x→-4)

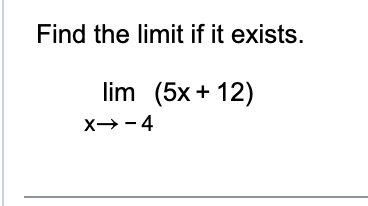
Find the Limit of: 5Lim x (x→-4) + Lim12 (x→-4)

5(-4) +12 =-8

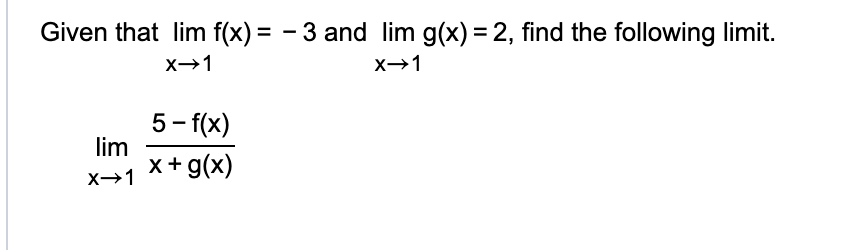
Solve:

• f(x) = -3

• x=1

• g(x)=2

5-(-3)/1+2= 8/3

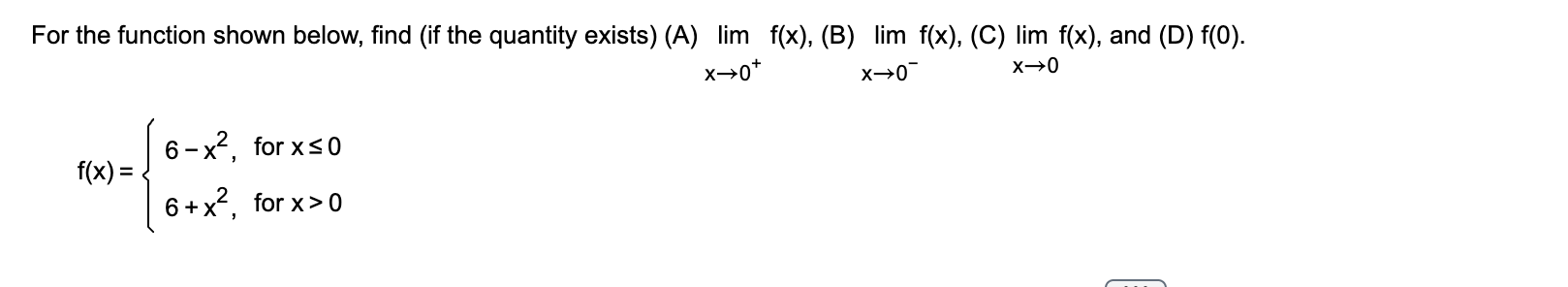
A) Lim→0+

6+(0)²

= 6

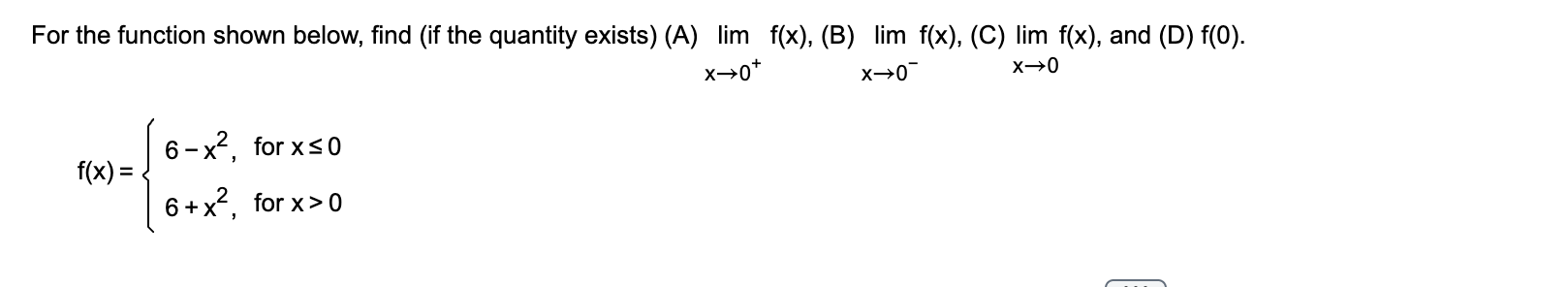
B) Lim →0-

6-(0)²= 6

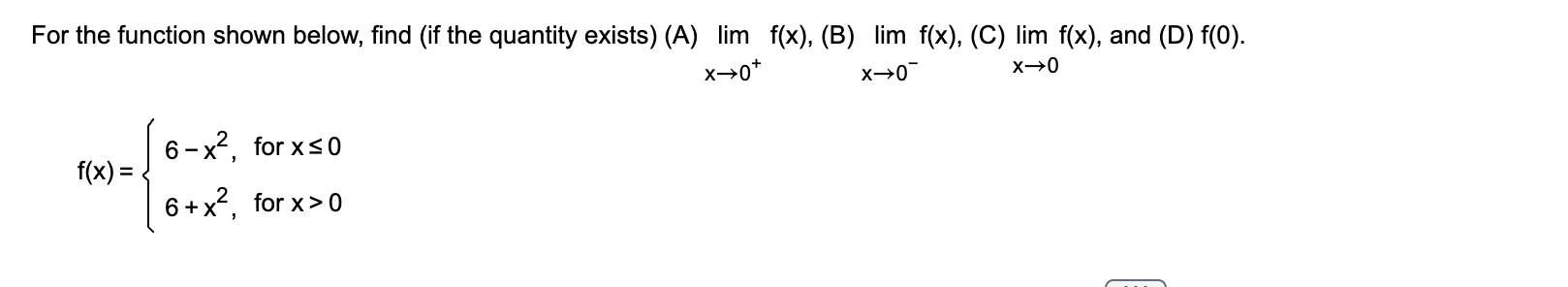
C) Lim→0

= 6

A) Lim x→5

Factor 4x²-19x-5:

4x-5: -20, find two values that multiply to -20 and add -19: 1 and -20

• (4x²+x)-(20x+5) → x(4x+1) -5(4x+1) → (4x+1)(x-5)

Factor x²+11x-80: (x+16)(x-5)

A) Both (x-5)s cancel out: (4x+1)/(x+16)

• 4(5)+1/5+16 = 21/21=1

B) Lim x→0

Use (4x+1)/(x+16)

• 4(0)+1/0+16= 1/16

C) Lim x→1

Use (4x+1)/(x+16)

• 4(1)+1/1+16= 5/17

Infinite Limits

These are infinite limits

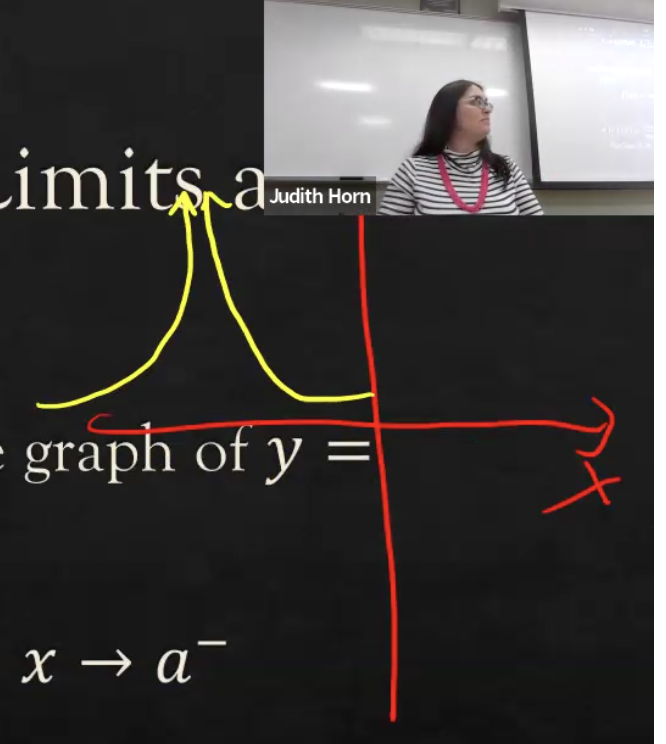
Vertical Asymptote

These are vertical lines that a graph approaches but never touches or crosses as the input (usually x) gets very close to a certain value.

Find the VA:

(x+3)(x-5)/(x+1)(x-1)(x+7)

The vertical asymptotes occur where the denominator equals zero, so set (x+1)(x-1)(x+7) = 0, which gives x = -1, 1, -7.

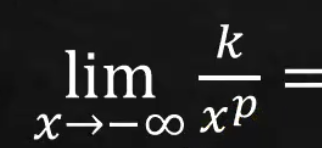
=0

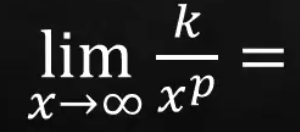
=0

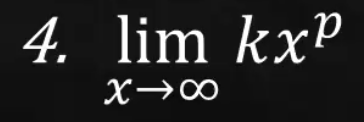
= positive infinity

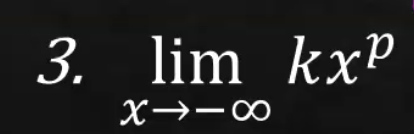
= both positive and negative infinity

Lim x→infinity: -7x² =

a negative infinity

Lim x→infinity: 7x² =

a positive infinity

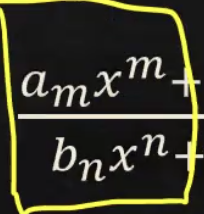
m>n

No horizontal asymptote

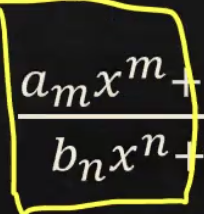
n>m

y=0

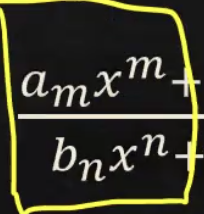
n=m

divide by the leading coefficients

Write the equation of a line with slope being -2 and points (3,5)

y-y1=m(x-x1)

• y-(5)=-2(x-(3)

• y-5=2x+6

  y=2x+11

Write y=2x+11 in standard form \

2x+y=11

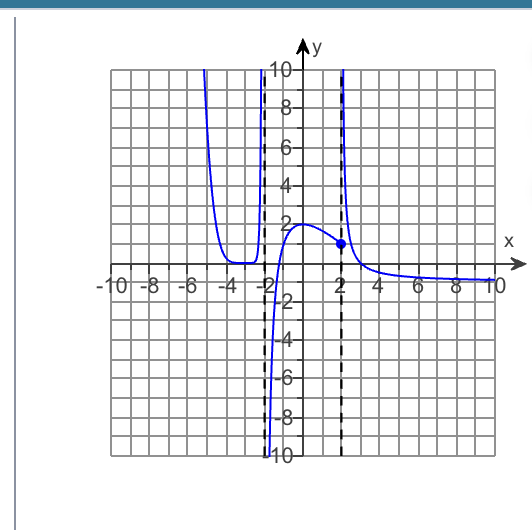
Find Lim f(x) x→ infinity

! Find whatever value the line is getting closest to as it’s moving towards infinity!

x= -1

6x/x-8

A) Find lim x→8⁻

• Coming from the left : negative infinity

6x/x-8

B) Find lim x→8^+

• Coming from the right : positive infinity

6x/x-8

C) find lim x→8

It doesn’t exist as there are differnet values

(A): f(-6)

• Plug equation into “y=”

• See what value you get at -6: -0.042

(B): f(-12)

• plug equation into “y=”

• See what value you get at -12: -0.018

(C): Negative infinity

• plug equation into “y=”

• See what value you are getting to as you get move negative, which is “zero”

(A) Horizontal Asy

• Both the num and dem have the same degrees: (2/1=1): y=2

(B) Vertical Asy

• X+4 =0, Vertical Asy: y=-4

(A) Horiztontal

• Higher degree on num, top kills twink y=0

(B) Vertical

• x-6=0

• VA: x=6

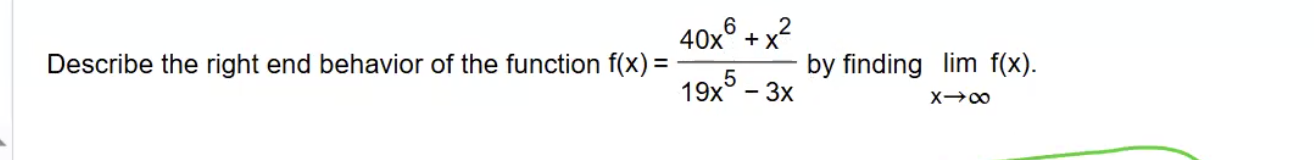
Describe right end-behavior

• Look at the leading terms

• There both positive (when dividing by two positives: you get a positive)

• Therefore, as you're going to positive infinity, the function is going to be positive infinity as well

! if it was -40/19: it would be heading towards negative infinity ! (Negative / Positive: Negative)

A function is continuous when...

its on an open interval

Open interval

unfilled circles: ( )

Closed interval

filled circles: [ ]

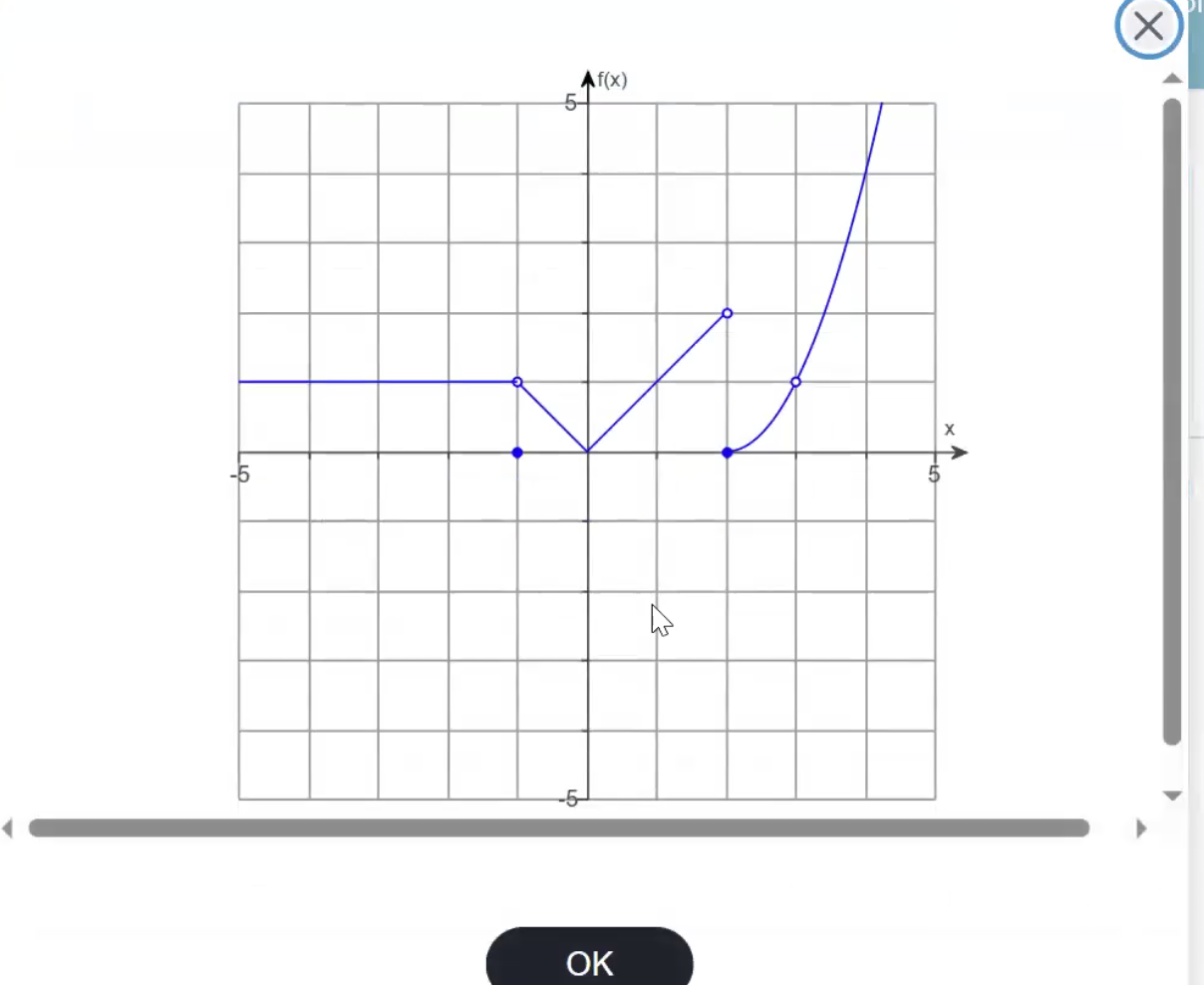
Coming in from the right: What is the estimated value? At f(-1.1)

Its approaching one

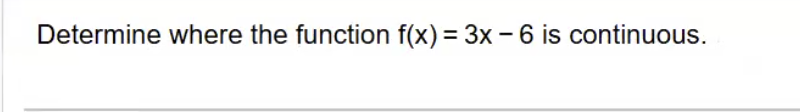
Determine where the function is continuous

• This is a polynomial

(-infinity, positive infinity)

Use a sign chart for: x²-5x-36<0, write in inequality and interval form

• Plug the equation into “y=” and find the zeros (9,-4)

• Notice how between those values (-4 to 9) its all negative or less than zero

• Inequality (less than zeros and values between -4 and 9) → -4<x<9

• Interval: (-4,9)

Notes for this problem

Since its square root its going to greater than or equal to zero

• For interval and inequality notation: Its going to involve brackets

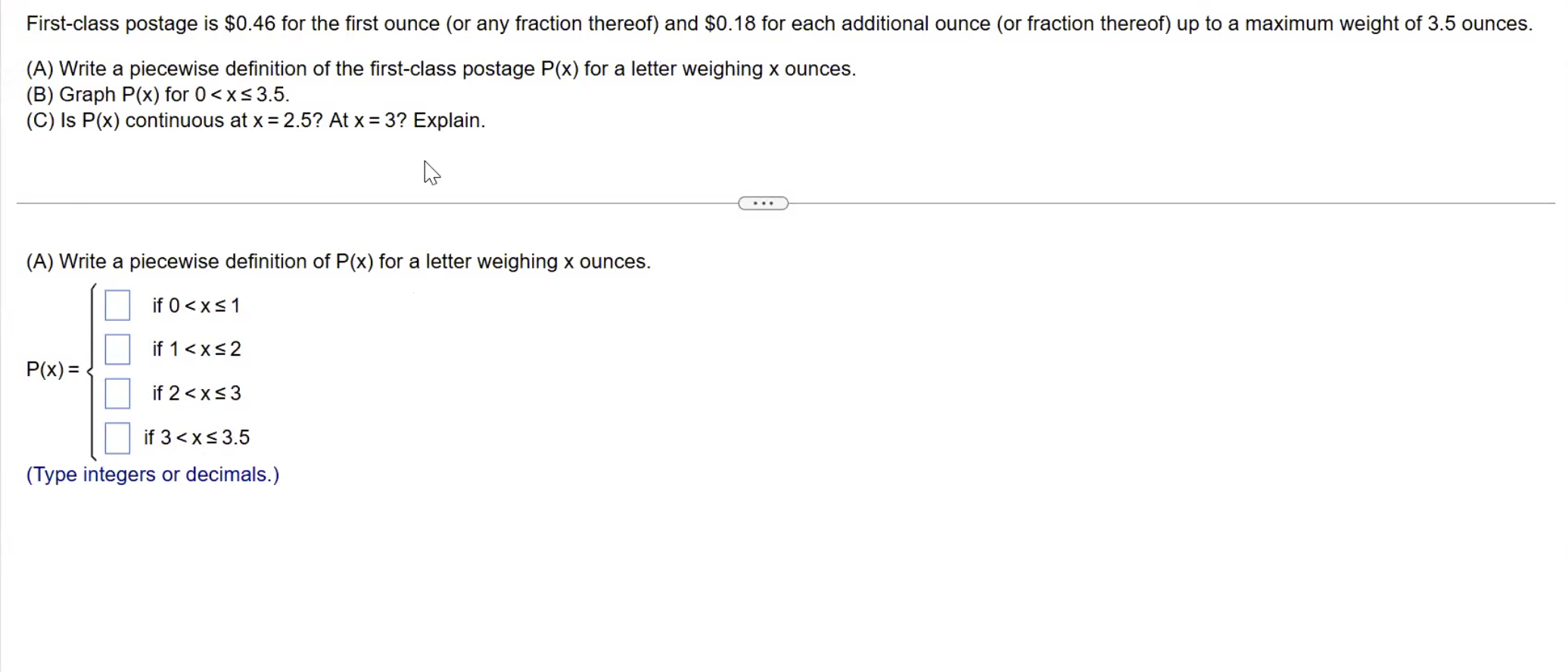
(A)

• The starting point is 0.46

• You keep on adding 0.18, because itadditional to new answer

• 0.46

• 0.46+ 0.18= 0.64

• 0.64 +0.18= 0.82

• 0.82+ 0.18= 1