Calc III Exam II Prep

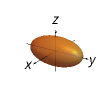
(x^2/a^2)+(y^2/b^2)+(z^2/c^2)=1

Ellipsoid (All traces are ellipses)

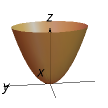
z=(x^2/a^2)+(y^2/b^2)

Elliptic Paraboloid (Made of ellipses and parabolas)

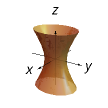
(x^2/a^2)+(y^2/b^2)-(z^2/c^2)=1

Hyperboloid of one sheet (connected)

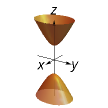
(-x^2/a^2)-(y^2/b^2)+(z^2/c^2)=1

Hyperboloid of two sheets (disconnected)

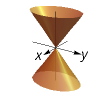
(x^2/a^2)+(y^2/b^2)=(z^2/c^2)

Elliptic Cone (Two inverted cones touching tips)

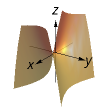
(x^2/a^2)-(y^2/b^2)=z

Hyperbolic paraboloid (Two hyperbolas connected)

x to spherical

x = ρ cos***θ*** sinφ

y to spherical

x = ρ sin***θ*** sinφ

z to spherical

x = ρ cosφ

ρ^2 = ?

ρ^2 = x^2 + y^2 + z^2

Spherical integral

∫∫∫ p^2sinφdφdρd***θ***

Linear Approximation

L(x,y) = f(a,b) + fx(a,b)(x-a) + fy(a,b)(y-b)

Average Value

(1/b-a)(1/d-c) ∫∫f(x,y)dydx (from a to b and from c to d)