RMA Week 10: distributions and z-scores

when are density curves useful?

when dealing with lots of participants, generalising results to the population

what is a density curve?

a histogram distribution of scores of participants. they use a mathematical model to describe how the scores of all participants in the population are distributed.

state 2 facts about density curves

1. the more real data points, the better the fit to the curve

2. ignore outliers and extreme values

to what side is the peak if a distribution is positively skewed

the left

to what side is the peak if a distribution is negatively skewed

the right

what axis are distributions always presented on

the horizontal (x) axis

what will the area under the curve always exactly equal

1

give an example of how you can make predictions about the overall population if you know certain values of the model (mean or SD)

if the area above the mean = 0.6, 60% of scores will be above the mean

what’s the median on a distribution graph

the point that divides the area into two equal parts - 50% above and 50% below

what are quartiles on a distribution graph

points that divide the area under the curve into quarters - 25% below Q1 and 25% above Q3

what is the mode on a distribution graph

positions at the peak of the curve

what is the mean on a distribution graph

the balancing point of the curve - e.g. - positive deviations from the mean match negative deviations

what are the positions of mean, median and mode on a normal distribution

mean = median = mode (all in the middle)

what are the positions of mean, median and mode on a positively skewed distribution

mode, median, then mean

what are the positions of mean, median and mode on a negatively skewed distribution

mean, median, then mode

what symbol is the sample mean for a distribution

x̄

what symbol is the population mean for a distribution

μ

what symbol is the sample SD for a distribution

S

what is the population SD symbol for a distribution

σ

describe a normal distribution in 5 points

1. symmetrical

2. single-peaked

3. the tails meet the x-axis at infinity

4. location determined by its mean

5. shape determined by SD

what are standard scores (z-scores) used for

• comparing values from different data sets

• when we know the mean and SD of the population

• not when taking samples

• e.g. is a score of 50 in RMA the same as 50 in RMB when they have different means and SDs?

how do z-scores solve the comparison problem between the data sets

by translating both data sets into a standard normal distribution - standardising the data

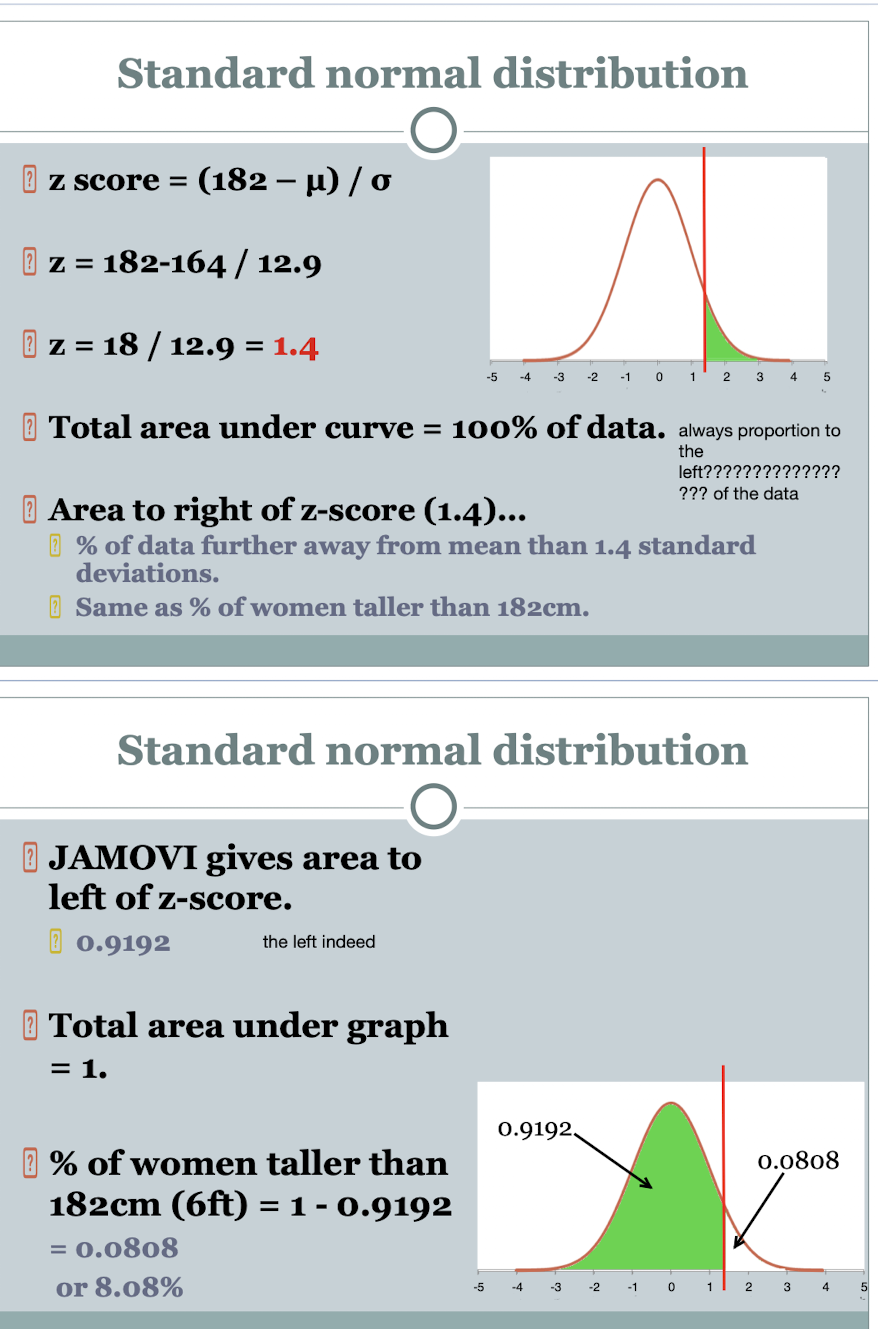
how do you calculate a z-score

the number of SDs that the observation deviates from the mean

• Z = deviation of x (the score you’re looking at) from (sample or population) mean / (sample or population) SD

• z = x - x̄ / S

how would you calculate a z-score on a graph with the selected figure, population SD and population mean

(score - mean) / SD