Review

Parent rational function

f(x) = 1/x

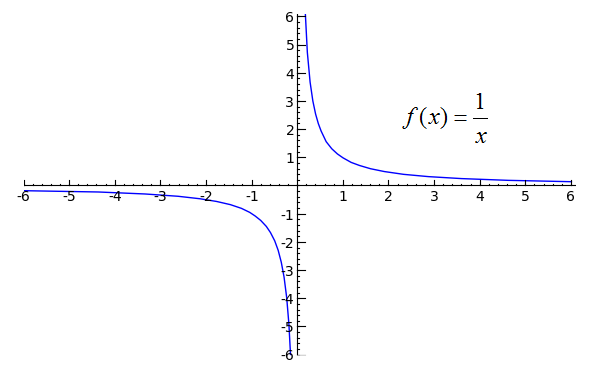
Piecewise function

Arithmetic function

aₙ = d(n - 1) + a₁

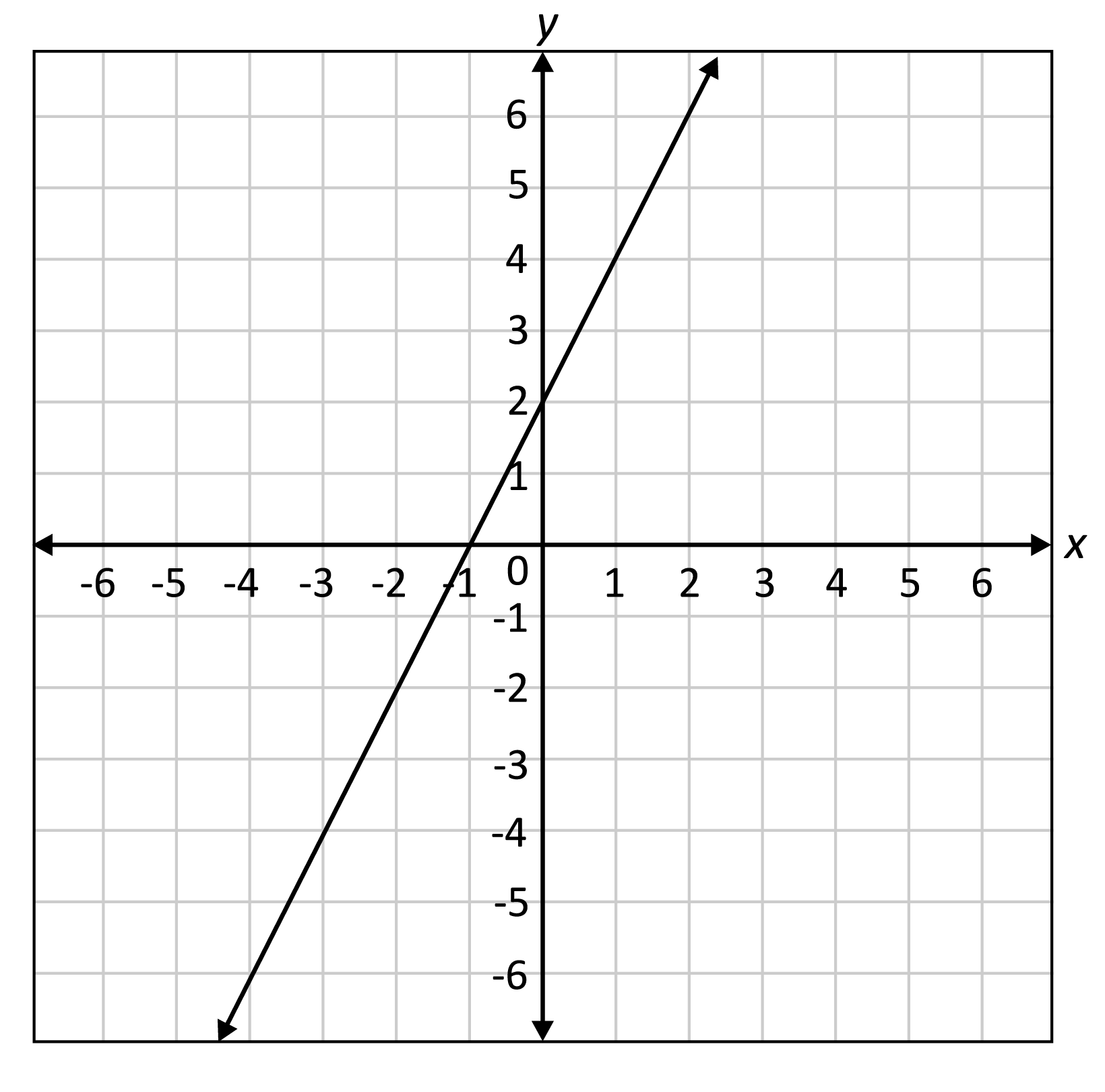
Geometric function

aₙ = a₁ ⋅ (rⁿ ⁻ ¹)

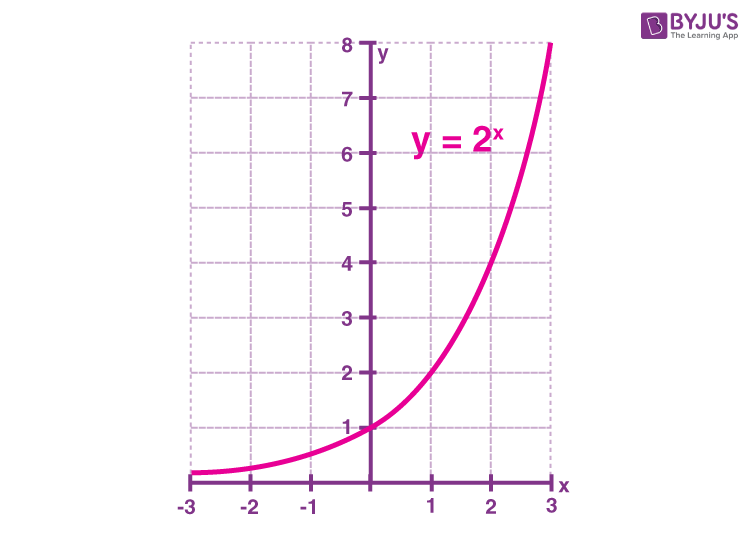
Finding an exponential function w/ two points

y₂ = y₁ ⋅ b⁽ˣ₂ ⁻ ʸ₁⁾

Logarithmic function

y = log_bx

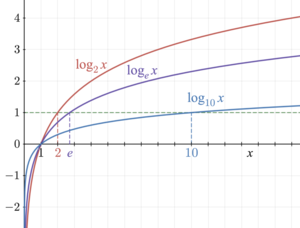
Circumference of a circle

2πr

Arc length

r(θ)

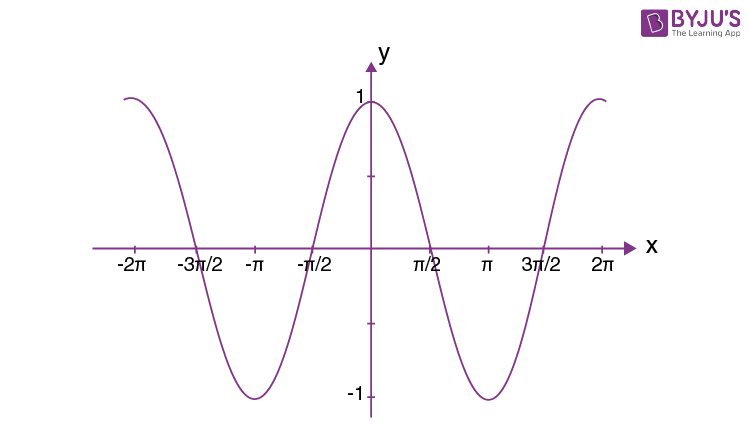
Cosine function

f(θ) = acos(bθ ± c)+ k

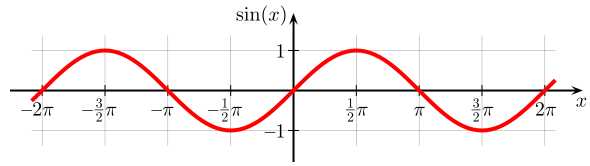
Sine function

f(θ) = asin(bθ ± c)+ k

Period of sine/cosine functions

2π/b

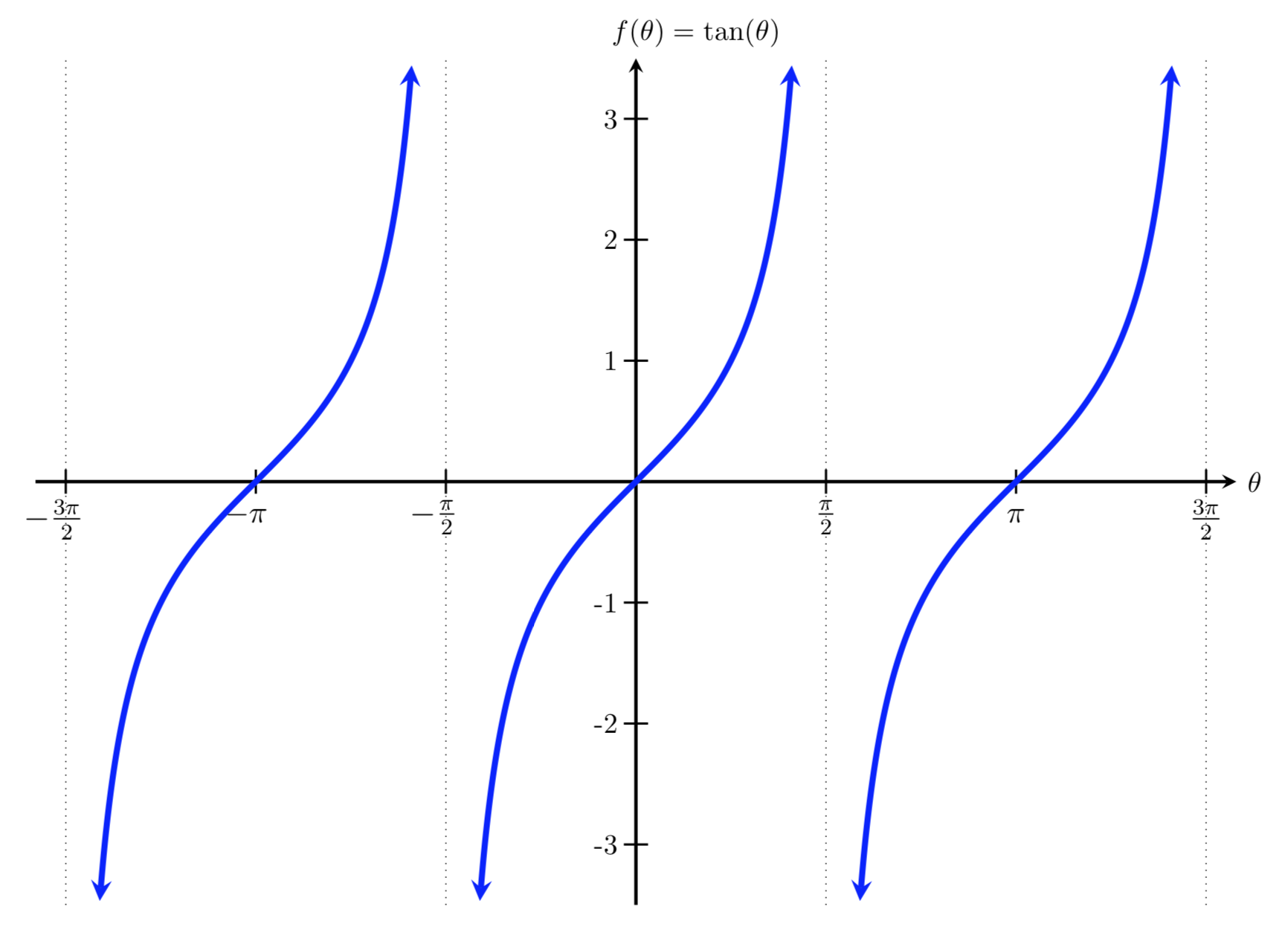
Tangent function

f(θ) = atan(bθ ± c)+ k

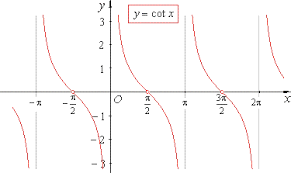
Cotangent function

f(θ) = acot(bθ ± c)+ k

Secant

sec = 1/cos

Cosecant

1/sin

Cotangent

1/tan

---

cos/sin

sin(α ± β)

sin(α ± β) = sinαcosβ ± sinβcosα

cos(α ± β)

(α ± β) = cosαcosβ ∓ sinαsinβ

1

sin²θ + cos²θ = 1

sec²θ

1 + tan²θ = sec²θ

csc²θ

1 + cot²θ = csc²θ

Polar to rectangular

x = r ⋅ cosθ

---

y = r ⋅ sinθ

Rectangular to polar

r = √a²+b²

---

θ = tan⁻¹(y/x)

Complex rectangular

a + bi

Complex polar

r(cosθ + isinθ)

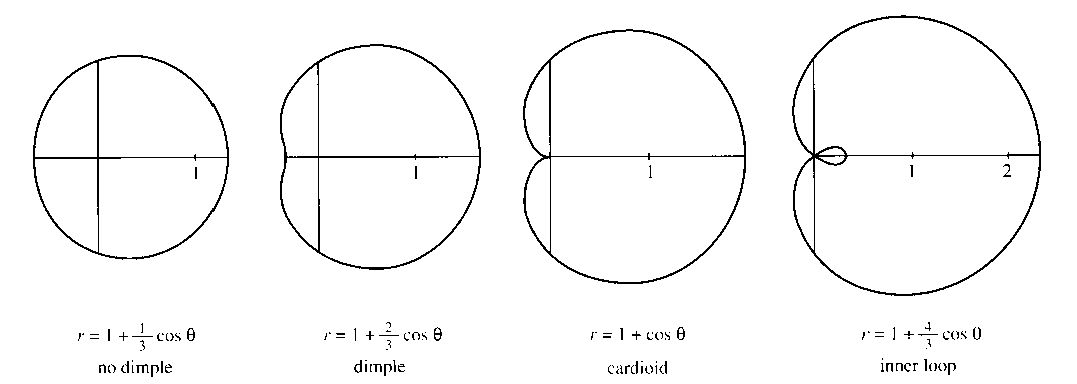
Limaçons

r = a ± bcosθ

---

r = a ± bsinθ

Circles

r = acosθ

---

r = asinθ

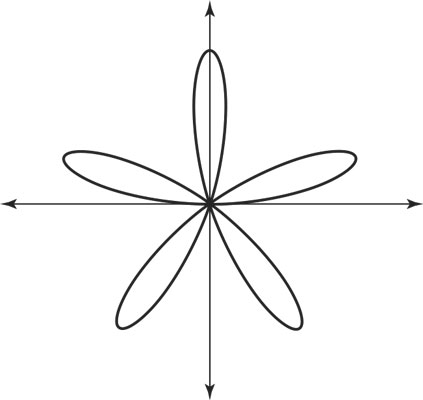
Roses

r = acos(nθ)

---

r = asin(nθ)

ROC of polar functions

(r₂ - r₁) / (θ₂ - θ₁)