Calculus II Chapter 7

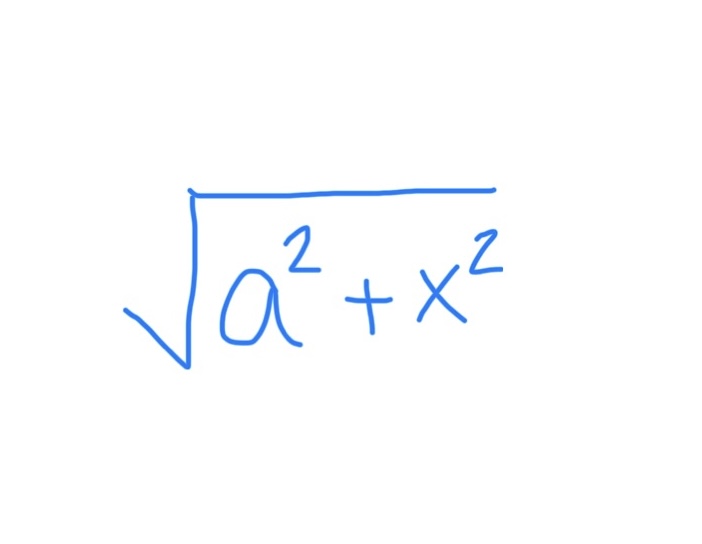
If you see this, use…

x = atanθ

dx = asec²θ dθ

1 + tan²θ = sec²θ

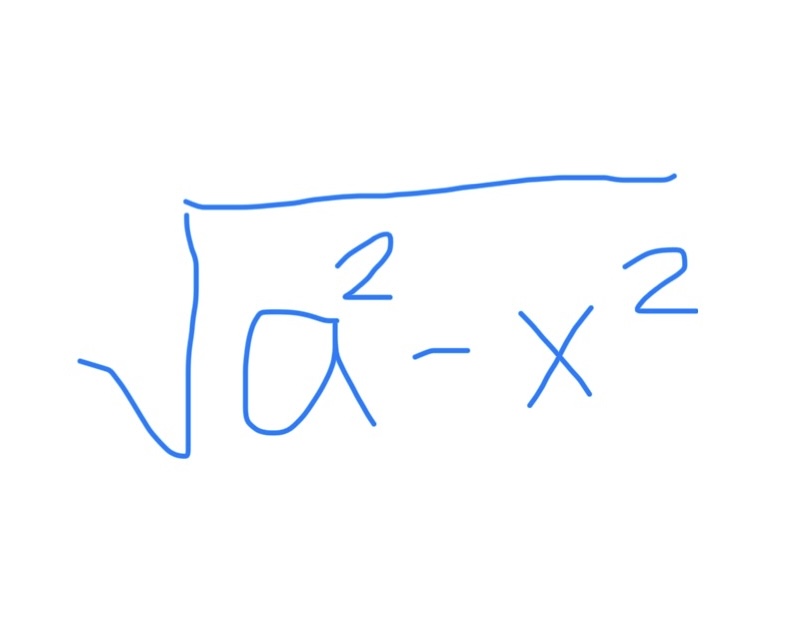
If you see this, use…

x = asinθ

dx = acosθ dθ

1 - sin²θ = cos²θ

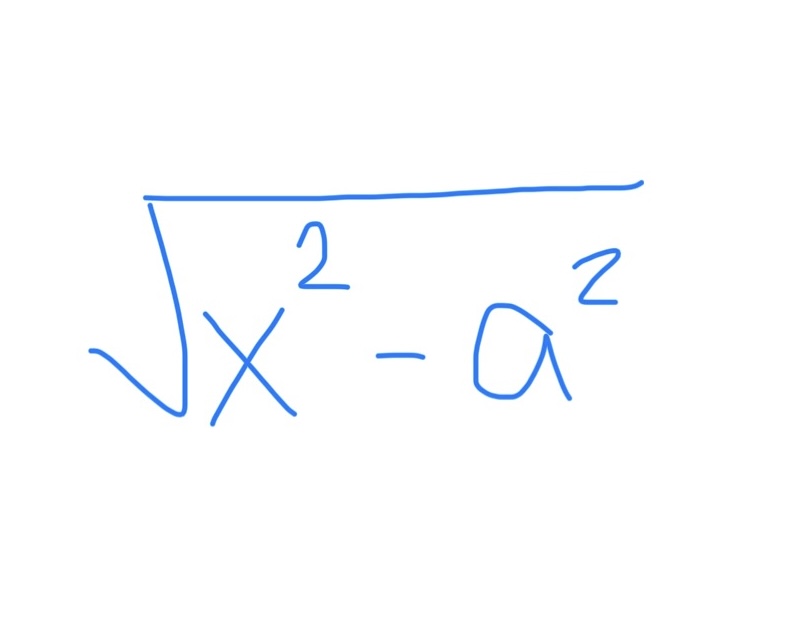
If you see this, use…

x = asecθ

dx = asecθtanθ dθ

sec²θ - 1 = tan²θ

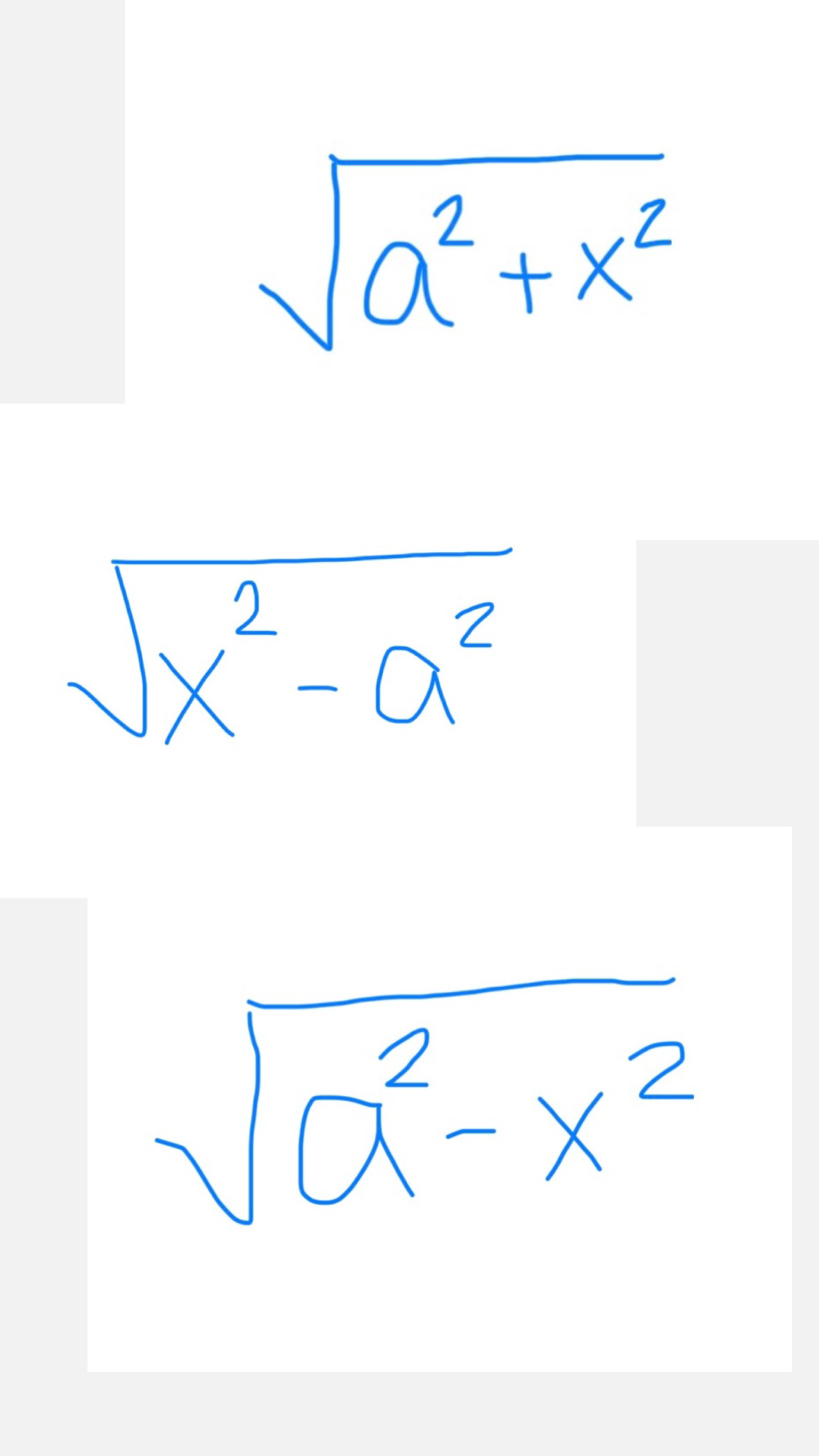
Evaluating Integral with

1. Find specific strategy and plug into x and dx

2. If possible, take out constant GCF

3. Replace with Pythagorean trig identity

4. Cancel out terms

5. Look at initial x = __ and isolate the trig function

6. Create triangle and plug in sides

• final unknown side is original sqrt in eqn

7. Replace answer with triangle values

Evaluating Integral where Num and Denom are Reduced Polynomials

• no common factors

• Deg T < Deg B

1. Factor num and denom

2. Separate eqn into 2 fractions added to each other whose denominators are each factor and numerator are variables

• Linear denom = A, B, C … numerator

• Quadratic denom = (variable)(x^one less degree) continue until get lowest degree

3. Set original equation equal to this

4. Multiply everything by original denominator to cancel out terms

5. Solve for each variable by systems of eqns

6. Plug in results for each variable into setup from Step 2

7. Integrate

∫ cos²θ

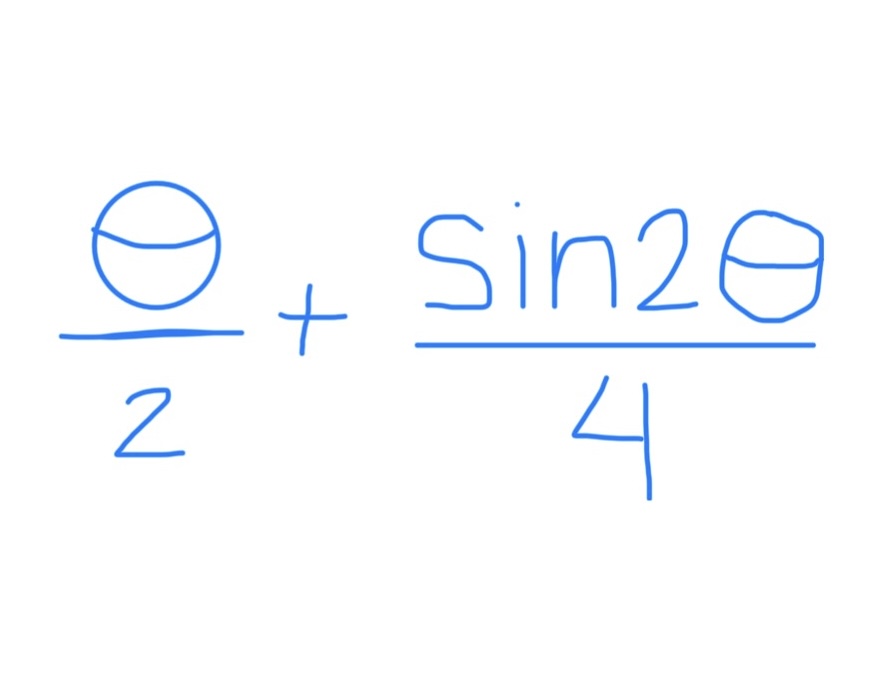
∫ sin²θ

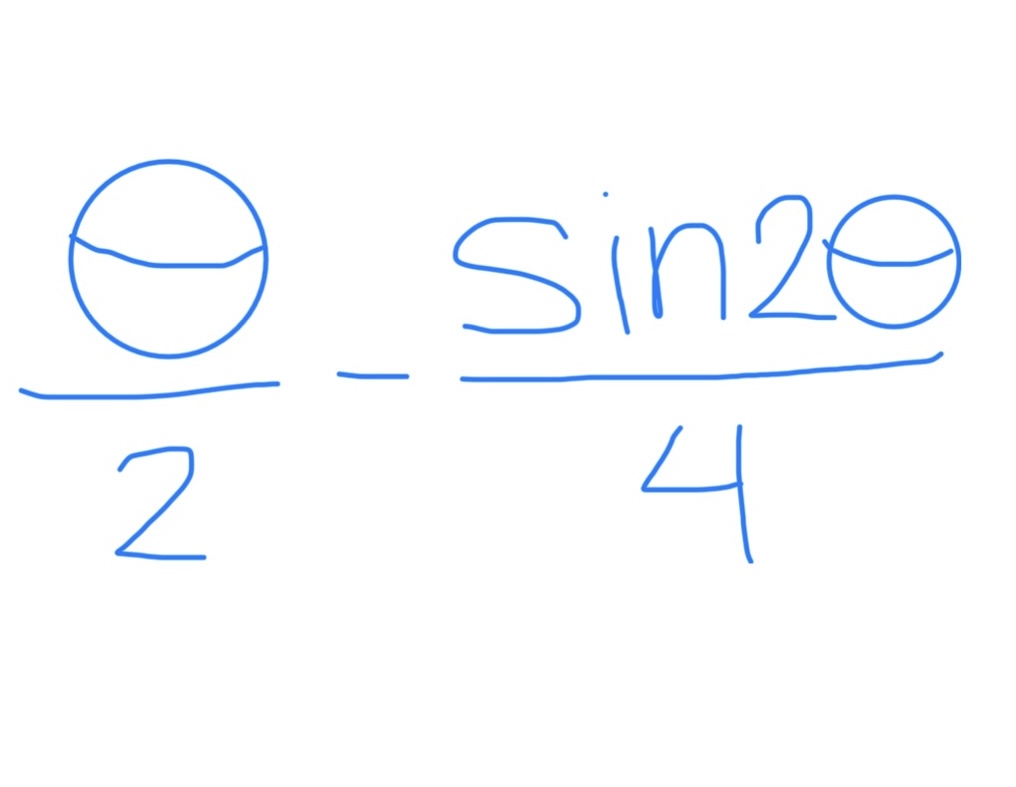
Use Table for Repeating Integration by Parts With…

xⁿsinx

xⁿcosx

xⁿe^x

Evaluating Integrals with Repeating Integration by Parts

1. Identify u and dv using LIATE

2. Create table

3. Find derivatives under u and antiderivatives under dv until you reach 0

4. Multiply diagonally and the combination of this is your answer

• the table goes +, -, +, - downward

What is Antiderivative of e^ax?

1/a e^ax

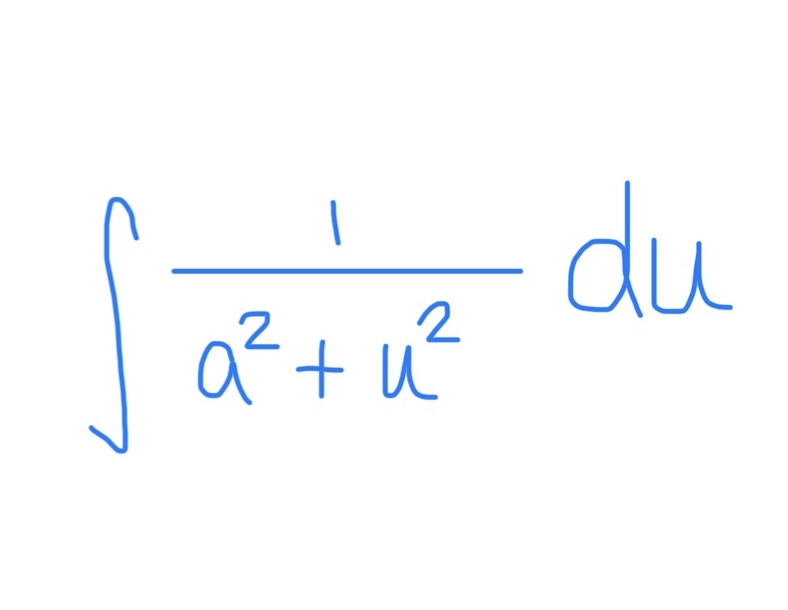
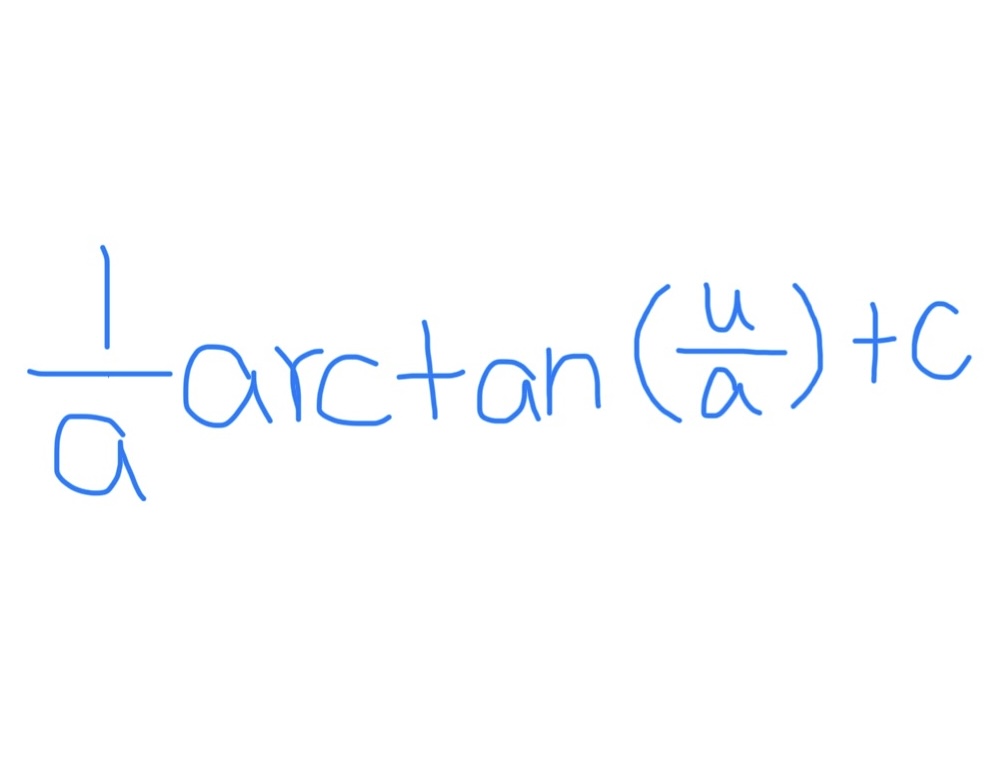
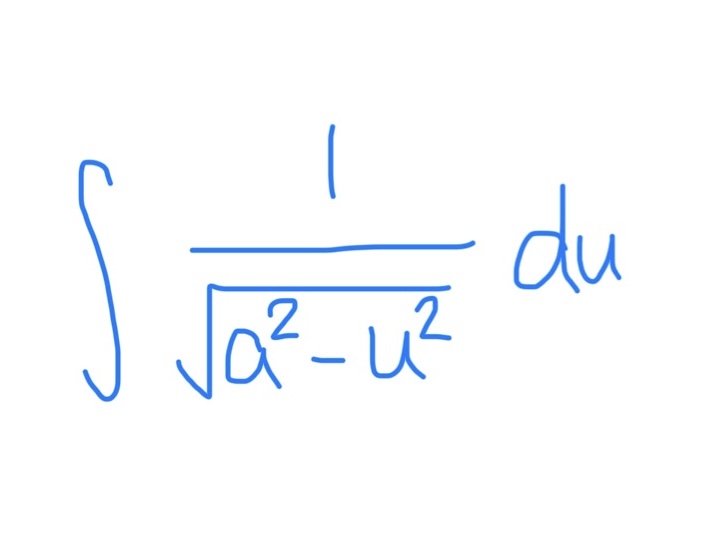
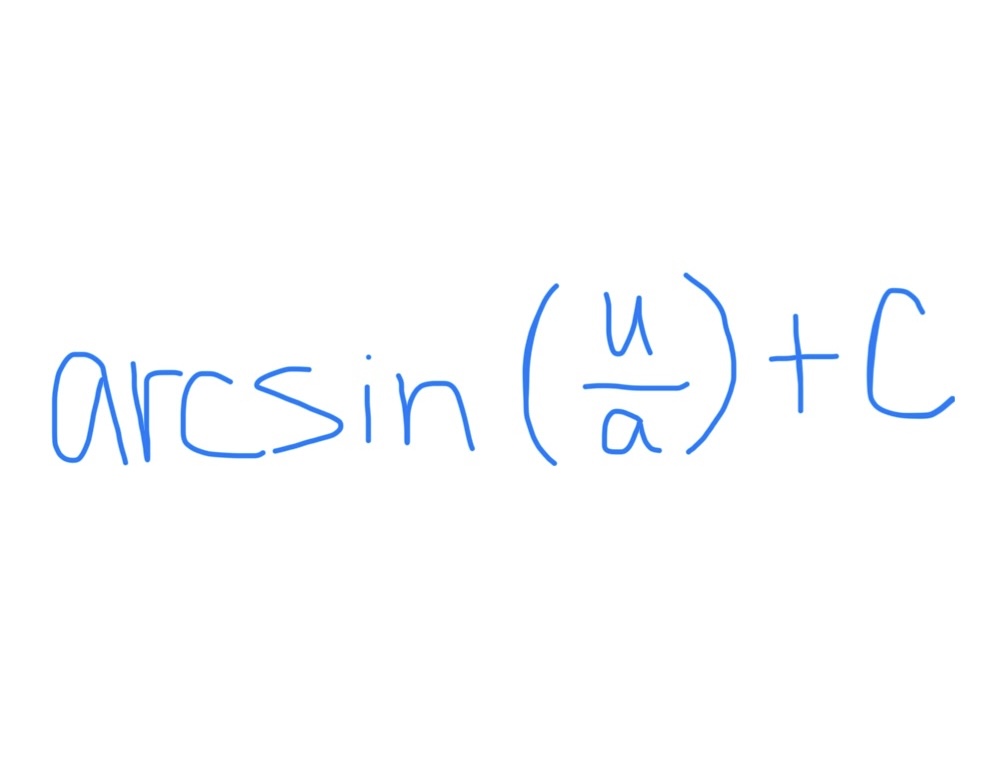
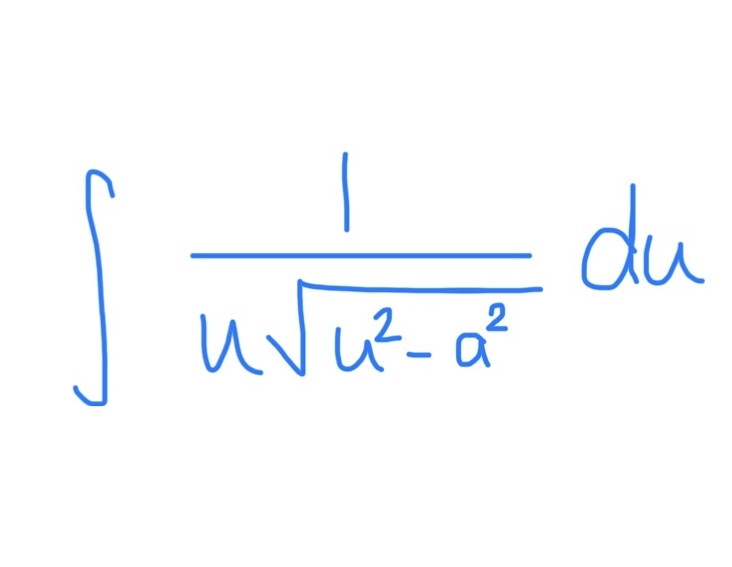
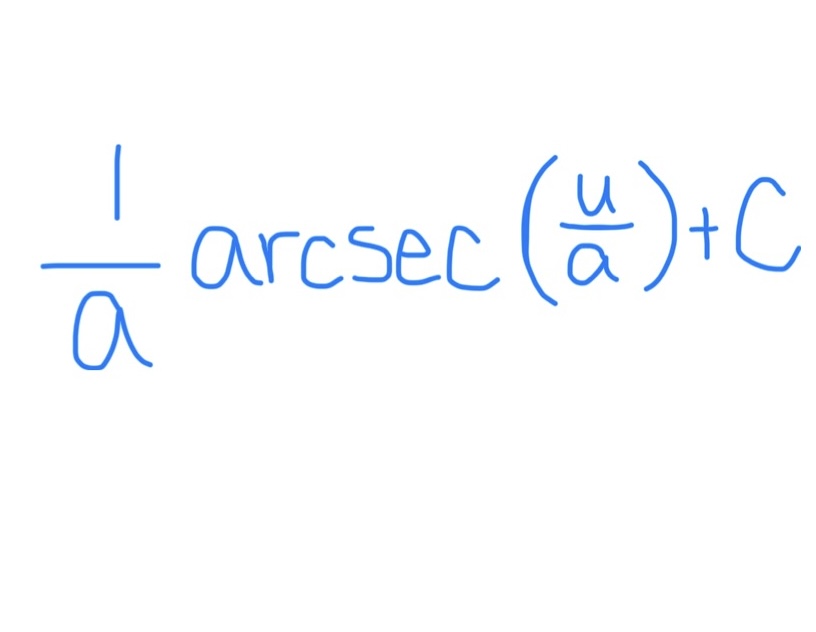
∫ tan(u) du

Ln |sec(u)| + C

∫ cot(u) du

Ln |sin(u)| + C

∫ sec(u) du

Ln |sec(u) + tan(u)| + C

∫ csc(u) du

-Ln |csc(u) + cot(u)| + C

∫ sin(u) du

-cos(u) + C

∫ cos(u) du

sin(u) + C

∫ sec²(u) du

tan(u) + C

∫ sec(u)tan(u) du

sec(u) + C

∫ csc(u)cot(u)

csc(u) + C

∫ csc²(u) du

-cot(u) + C

Derivative of arctanx

1 / 1+x²

Derivative of arcsinx

1 / sqrt(1-x²)

When To Use Integration by Parts?

… when you’re dealing with:

xⁿsinx, xⁿcosx, xⁿLnx, arctanx, arcsinx, arcsecx, xⁿe^x, e^xsinx

Evaluating Regular Integration by Parts Integrals

1. Determine u and dv using LIATE

2. Rewrite eqn as uv - ∫ v du

3. Solve solvable integrals

Identifying Circular Integration by Parts

When one step will spit out a previous function or the original function

Evaluating Circular Integration by Parts Integral

1. Determine u and dv using LIATE

2. Rewrite eqn as uv - ∫ v du

3. Solve, but when you get result that is the original eqn, take what you have so far and set the original eqn as I and then set everything equal to I

4. Solve for I to get answer

How to Integrate ∫ sinⁿ(x) cosⁿ(x) dx Where There’s an Odd Power on Sin(x) or Cos(x)

1. Pull out a factor from whichever trig has odd power and put it with dx

2. Replace odd trig using sin²(x) + cos²(x) = 1

3. Trig function that wasn’t odd is u

   • cos(x) = odd

     • u = sin(x), du = cos(x)

   • sin(x) = odd

     • u = cos(x), du = -sin(x)

How to Integrate ∫ sinⁿ(x) cos^m(x) dx Where Both Powers are Even

Use power reduction formulas

• sin²(x) = (1-cos(2x)) / 2

• cos²(x) = (1+cos(2x)) / 2

1. Deconstruct all trig into (__)²

2. Replace w/ power reduction formulas

3. Integrate

How to Integrate ∫ tanⁿ(x) sec^m(x) When Power of Sec(x) is Even

1. Pull out a factor from sec(x) so that it becomes sec²(x) and put it with dx

2. Replace rest of sec(x) with sec²(x) = tan²(x) + 1

   • except the sec(x) that’s part of dx

3. Do u-substitution where

   • u = tan(x)

   • du = sec²(x) dx

How to Integrate ∫ tanⁿ(x) sec^m(x) When Power of Tan(x) is Odd

1. Pull out a factor from tan(x) so that it becomes tan²(x) and put it with dx. Also pull out a factor from sec(x) and put it with dx

2. Replace rest of tan(x) with tan²(x) = sec²(x) -1

3. Do u-substitution where…

   • u = sec(x)

   • du = sec(x)tan(x) dx

How to Integrate Individual Trig Functions with Even Powers

1. Use power reduction rule

   • sin²(x) = (1-cos(2x)) / 2

   • cos²(x) = (1+cos(2x)) / 2

2. Then use u-du integal

How to Integrate Individual Trig Functions with OddPowers

Use u-du integral