Lecture 7 - Repeated Measures ANOVA

Difference in between subjects and within subjects

Within subjects = repeated measures

• Between subjects: Each person assigned to one condition only one goal per person  

• Repeated measures: same people providing multiple observations in multiple conditions at different times  

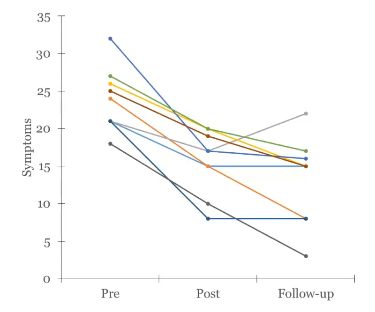
You run a study on PTSD treatment pre, during, and post…. Describe the between-subjects and within-subjects variability 

There is a lot of between-subjects variability (people are just different from eachother on average)

Looking at the mean, there is a change over time → within-subject variability across the three measures (change within a subject)

What does partitioning variance mean

In ANOVAs, in the total variability of the DV we want to know how much of the variability is between subjects vs within subjects

• We also want to know how much within subjects variability is due to the treatment effect and how much is just error left over

• We use a source table to partition variance

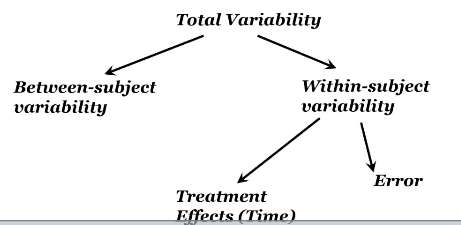
Source Table for within subjects ANOVA 

Between subjects → compute SS for between subjects to remove between subjects variability and have within subjects left over 

• Once we have within, we can divide it into error and time (repeated) 

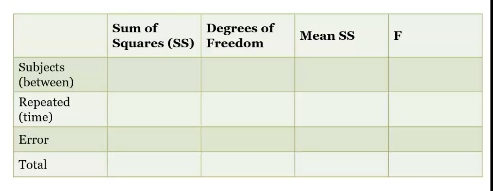
Calculating df

people vs observations (9 people = n) (number of total observations = N) 

SS total

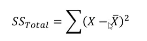
Calculating between subjects SS

need to know each persons mean (subject mean) *only fill out first two columns for this one (not mean SS or F)

Why dont we fill out SS or F for between subjects variability?

All it would tell us is that people in the sample are on average different from each other, which is almost always going to be the case so it’s not that interesting

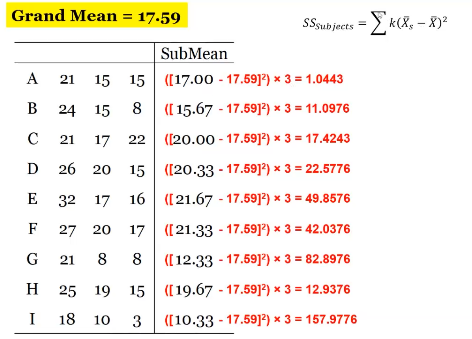
Repeated measures SS

Mean for each observation period 

• Whatever is repeated = time 

Error SS

Calculating mean SS

Dividing SS by df

Mean ss

Devide mean squared by the error term

• Now you can use the table (is it higher than the f critical)

What happens when you look at the table and the value is bigger than f critical

The means are different from eachother 

What would happen if you used a between subjects ANOVA

Total SS and repeated SS would be the same would be the same

• Error would be different 

• We can remove the variance due to individual differences which makes our error term smaller and have more power 

Why are btwn subjects stronger than independent or vise versa  

We can remove the variance due to individual differences which makes our error term smaller and have more power 

What are the three assumptions in a repeated measure

This test will work properly if…

1. Observations are normally distributed

2. Population variances are equal (homogeneity of variance)

3. Observations are no longer independent → Compound sphericity of the variance and covariations matrix

What does this mean: At each time period you can compute a variance (diaginal)

What does Compound sphericity of the variance and covariations matrix mean?

Compound sphericity of the variance and covariations matrix

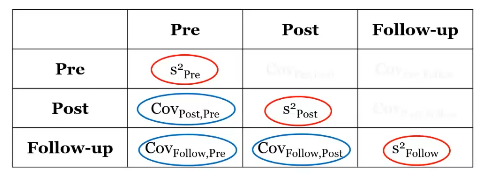
Correlation vs Covariance 

Covariance: the strength of the relationship between one variable and another (post and pre = pre and post, making it semetrical) → if the test is nonsignificant, it means all of them are the same, if it is significant, the test is violated

This assumption is often violated

• Similar to how variance and sd are if you now one you know the otehr 

• Same as correlation and covariance 

Mochlys Test of Sphericity

Are covariances equal of not 

• For eg if p=.274 (bigger than 0.05) it is non significant meaning covariances are equal (not statistically different) 

• Use sherisity assumed line

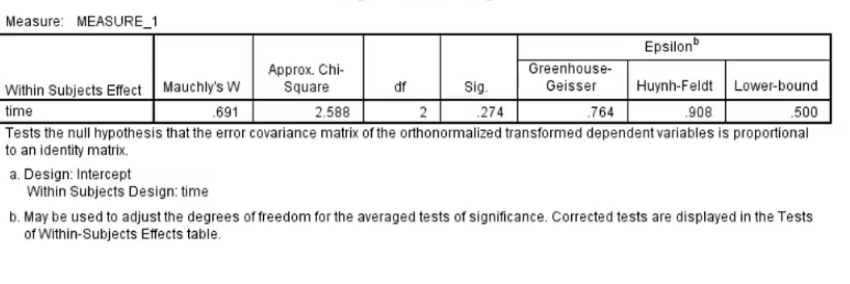
Greenhouse-Geisser

Used if Mauchly’s test is significant

If the compound symmetry assumption is violated, using F-test that assumes compound symmetry can inflate the type 1 error rate (have an effect when you don’t)

• Adjusts the df (fewer df)