Dynamic Bayesian Networks & Hidden Markov Models

basically about how bayesian networks can model sequences or temporal data, how to build HMMs (generate sequences / calculate useful probabilities)

what are dynamic bayesian networks

a probabilistic graphical model that captures systems' temporal dependencies and evolution over time.

• nodes represent variables (features) at distinct time slice

• there are directed links between nodes within the same time slice (BN) and between time slices (new)

  • e.g. lag between an observation in one feature and an observation in another

• often assumes 1st order Markov Assumption

• for a single time slice, the base network captures the conditional dependencies for a given point in time like a normal BN

e.g., 2 time slices, n features, can have auto-regressive links

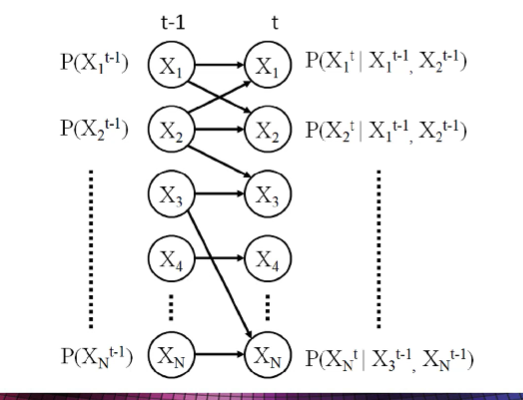
what is an auto-regressive link

a link from the same feature at a previous time slice to the feature at the current time slice

• the feature is influenced by its previous self

what are the ‘rules’ of DBN

• no cycles

• can’t have links going back in time

what is the 1st Order Markov Assumption

links only need to span adjacent time slices in order to make predictions over time

• e.g. link between T → T1, not a huge jump which causes complexity like T → T10

• links can’t jump over many time slices, only adjacent

what can we use DBN for

can still enter info and see the impact it has on the rest of the notes, even across different time points

• can come up with an explanation for while a current time point value has a certain value - explaining

• or make predictions on the future trajectory of the features - forecasting

what are Markov Chains

one of the simplest state-based models that links a number of possible state transitions over a sequence or time window

• models 1 variable as it changes over time

• H is a sequence of data being modelled

what do Markov Chains require

requires

• an initial probability distribution (PD for the states at the initial time slice)

• a transition probability distribution matrix (determines state changes over time given previous states)

assumes 1st order markov assumption where only immediate previous state is needed to calculate the next state p(ht|ht-1) which is the conditional probability

• where current state determines probability distribution of next stat

how can we calculate the probability of a sequence H using markov chains

H = 1, 2, 1, 2

P = 0.5, 0.1, 0.3, 0.1

transitions = initial 1, from 1 to 2, from 2 to 1, from 1 to 2

• the first value is always the initial state since there’s nothing to transition from, so use the probability from the initial probability distribution

• use the transition probability distribution values starting from the second value in the sequence

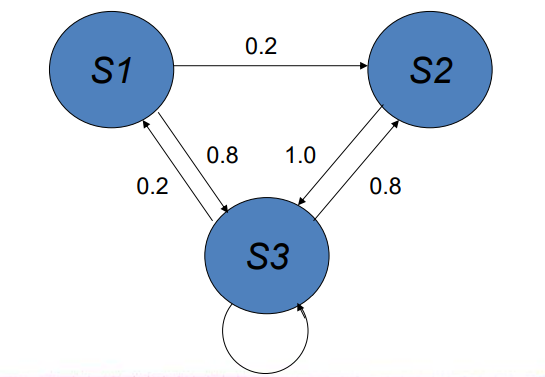
how can we visualise state transition probabilities

create a state transition diagram using the given markov chain and its state transition distribution matrix

• e.g. a markov chain with three states

what is a hidden state

underlying variables that generate the observed data, but they are not directly observable

e.g. in the example, the hidden state is which urn we have been given, we don’t know what we’ve been given but we can observe it

what are observations

the variables that are measured and observed

what is a hidden markov model (HMM)

used to model the probabilistic relationship between a sequence of observations and a sequence of hidden states

• generate sequences of observed states based on hidden states

what do HMMs require

• initial state distribution

• transition distribution - the probability of transitioning from one hidden state to another, using a Markov Chain H that represents the hidden states that the hidden variable transitions between over time

  • P(Ht |Ht-1 )

• emission distribution - the probability of observing an output given (conditioned upon) a hidden state, where observed nodes are X. linked directly to the hidden node in the same time slice

  • P(Xt |Ht )

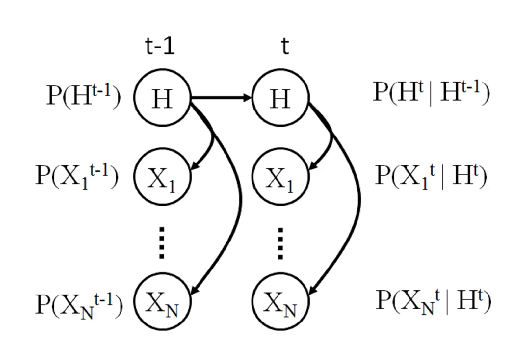
what is the graphical representation of a HMM

the H nodes are hidden, all we see are the observable X nodes, but we know that the X nodes are controlled in some way by the H hidden nodes

• this structure is fixed and not learnt from data like BN, just imposed

what are the benefits of the hidden state

can capture more complexities in the probabilities

what is the probability of the hidden state sequence {1, 2, 2}

= 1 × 0.2 × 0.6 = 0.12

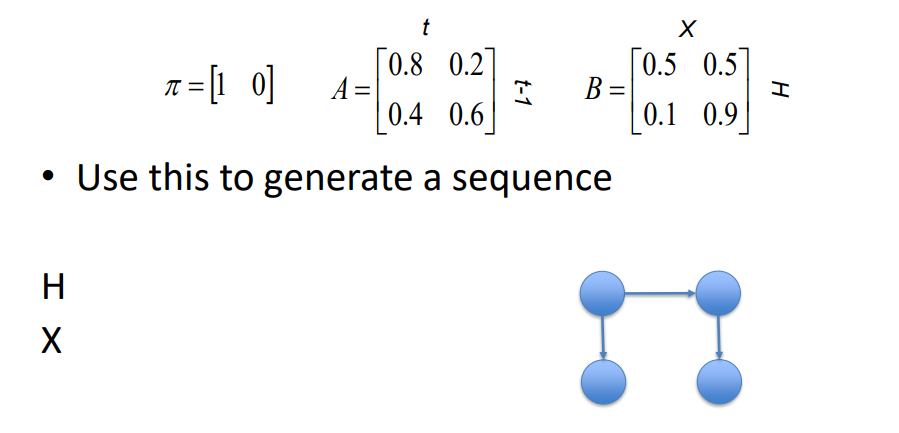
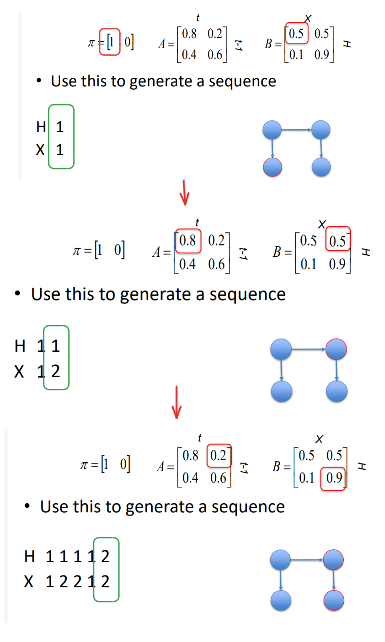
given this HMM set up, how can a sequence be modelled

1st loop:

• start with the initial state for H = 1 (since this model it can’t be 2)

• then based on H = 1, look at the emission probability for X, (since probably is both 50/50, its randomly chosen as 1

2nd loop

• since H is hidden, the value of if it transitions or not is based on its transition distribution, but we don’t change or choose this (imagine hidden state is acting by itself simulated with a random number generator), we just observe the new state H e.g. H is 1 again

• based on new state H, look at emission distribution to get the value for X e.g. 50 % change it could be in either state 1 or 2, (this can also be simulated to randomly choose, we are observing, not choosing)

3rd loop

• let’s assume H transitions to state 2 (on its own accord)

• then looking at the emission distribution, the probabilities for X being 2 are heavily biased to state 1 compared to before. so more likely it will be state 2.

what state sequence is most likely for the hidden state given the observed state

assume that the most likely state sequence always uses the state where the probably of each individual observation is max

• Heads - max is 0.75 in state 2

• Tails - max is 0.75 in state 3

therefore assume

• every H in sequence X comes from state 2

• every T in sequence X comes from state 3

final answer

• H = 2, 2, 2, 2, 3

what is the probability of the observation sequence AND the most likely hidden sequence

• H = 2, 2, 2, 2, 3

• X = H, H, H, H, T

times everything together

• 1st loop with state 2 and X = H = 0.3 × 0.75

• 2nd loop with state 2 and X = H = 0.3 × 0.75

• 3rd loop with state 2 and X = H = 0.3 × 0.75

• 4th loop with state 2 and X = H = 0.3 × 0.75

• 5th loop with state change to 3 and X = T = 0.5 × 0.75 (slides are incorrect)

times all 5 values together

what are some typical algorithms for HMMs

• forward algorithm

• most probable explanation using the Viterbi algorithm

• Learning using the Expectation Maximisation algorithm

what is the forward algorithm

Given an observed sequence, X and a known model (HMM), M, how do we compute the probability of seeing that sequence from the model?: p(X | M)

• helps us learn and parameterise the model

• basically, what’s the most likely model that fits the data

what is the Most Probable Explanation using the Viterbi algorithm

Given the observed sequence and the model, how do we choose an optimal hidden state sequence?

• how can we predict what the underlying hidden state sequence is given some observations

what is the Learning using the Expectation Maximisation algorithm

How do we adjust the model parameters to maximise the probability of the observed sequence given the model?

• how can we learn what the hidden parameters are

• used to do clustering where H is the hidden class variable which becomes the cluster variable

what are the applications of HMMs (and thus DBN)

• aligning sequences of nucleotides (genetic medicine)

  • Finding where sequences are the same

• text modelling, sequence of words

• speech recognition

• monitoring and tracking behaviours, e.g. modelling an elderly person in a house, classifying whether someone is sitting down or cooking based on the dynamics of an accelerometer to detect between normal and abnormal behaviour

• recognition of mouse gestures like swiping tapping recognition

what’s the difference between HMM and DBN

HMM are a specific type of DBN

• HMM are temporal models for time-series data where a single hidden state changes through time, influencing the observations

• DBN capture how dependencies among a wide range of relationships between variables change through time