6.1 - Area Between Curves

Area between curves are never…

Negative

The formula for finding area between curves

• You have to : (Top function - Bottom function )

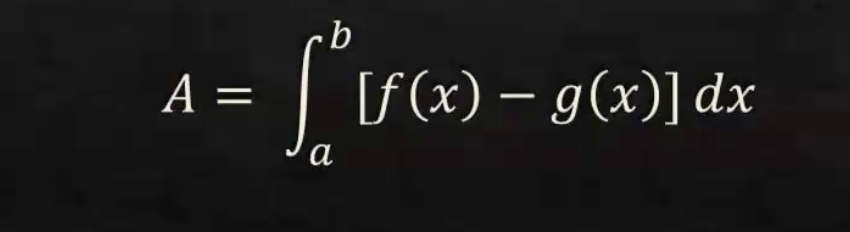
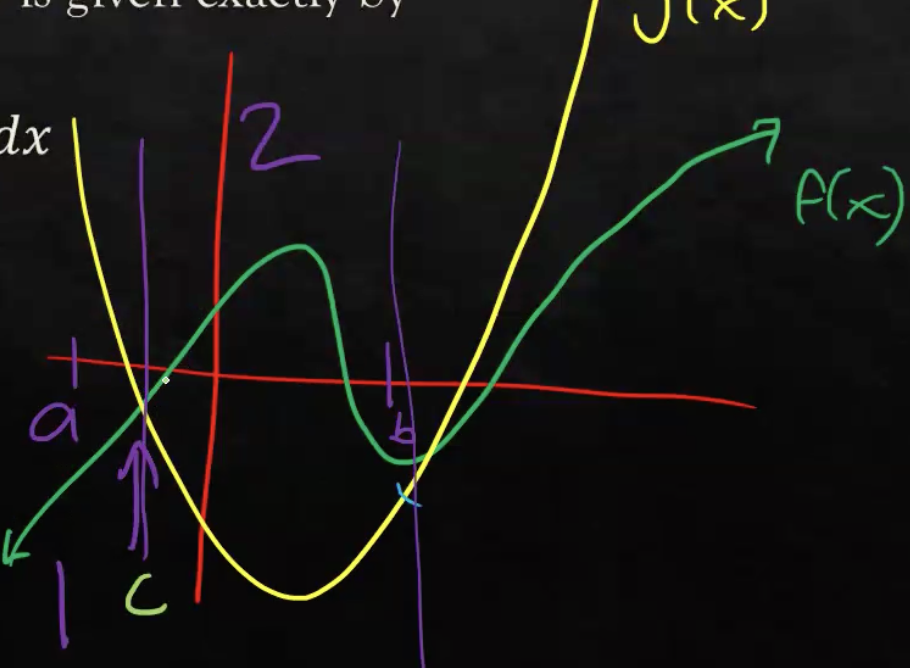
Write the definite integral from A-C

g(x) - f(x)dx : Yellow is the top function, green is the bottom

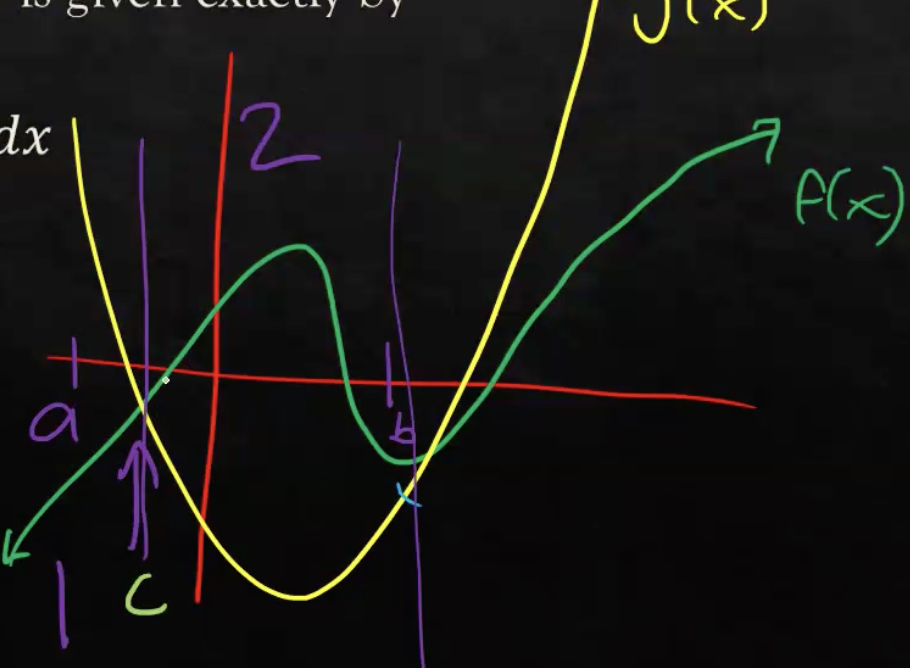
Write the definite integral from C-B

f(x) - g(x)dx: Green is the top function, yellow is the bottom function

Lorenz curves are used for

Regression analysis

Absolute equality

Area between curves is 0

Absolute inequality

Area between curves is ½

For Lorenz curves, how do you use the gini index?

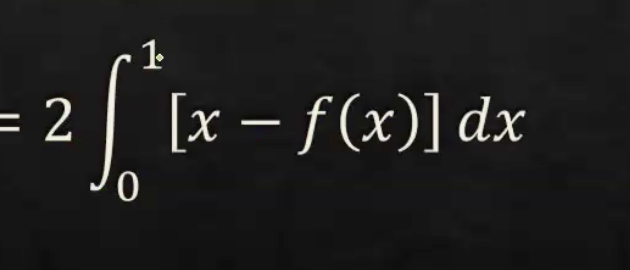
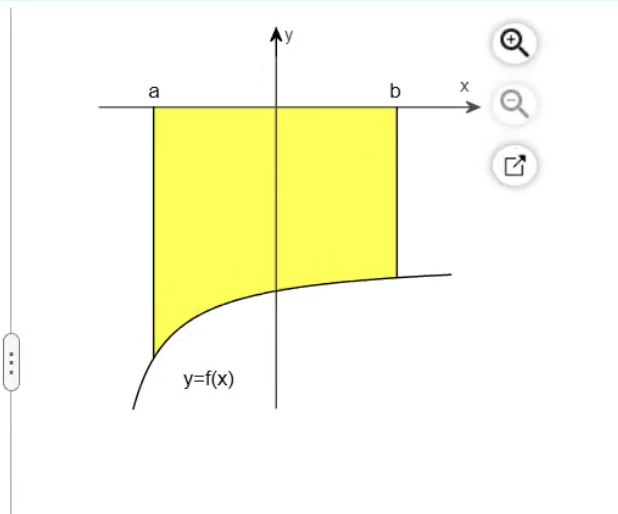
Set up the indefinite integral from a-b

! From a-b, its below the x-axis: its going to be negative !

a indefinite integral b: -f(x) dx

! for finding areas between curves, we use square units for our final answers !

Steps

1) Figure out which function is the top and bottom (in y=)

2) Write out the indefinite integral (top-bottom)

3) You can use MTH function 9, or find the antiderivative.

Find the area between the two curves

Steps

1) Figure out which functions is top and bottom, by plugging it into “y=”

2) For finding the area: its top-bottom

3) You can either fine the antiderivative, or plug the function into MTH (9)

Find the area between the curves

Steps

1) Figure out what function is the bottom and the top by using “y=”

2) For finding the area, top-bottom : from -1 → 2 [ (24) - (-4x+16) ] , simply the negative value into the second equation

2) (24) (+4x -16) → [8+ 4x] dx

3) Find the antiderivative. → 8x + 4 (x²/2)

4) Evaluate from -1 to 2. / Or plug the function into MTH 9

Finding the area of curves with absolute value

! With absolute value, it doesn’t matter what function is top or bottom!

Steps

1) MTH 9: Make sure you use the absolute value symbol for finding this answer

Find the area of curves with the interval [4,9]

Important Information: The interval means that its going from 4 → 9

Steps

1) MTH 9: From 4→9: [( 70/t + 7 +7) - (0) ] = you will have your answer

Finding the gini index for 1963 and 1983

1963

1) Its 2, from 0→ 1 (x-x^9)

2) Find the anti: x²/2 - x^10/10 from 0→1

In simpler forms: 2 (1/2 - 1/10)= 0.8

1983

1) Its 2, from 0→1 (x-x^11)

2) Anti: 2 (x²/2 - x^12/12)

In simpler forms 2 (1/2- 1/12) = 0.833

0.8 is more equally distributed since its closer to 0

What is the common rule for finding areas between curves?

Top function - Bottom function

How do you use the Gini index?

2 from 0→ 1: ( x- the function given)