L6: Spatial modeling

Arrow and spatial modeling

• Arrow shows that there is problem whenever we want to have coherent group choices and the fairness of the method of decision making

• What do I mean with fairness?

  • Do we believe that all preference orders are available to everyone

• One way to overcome this problem is to change the universal domain (Condition U) in such a way that a individuals preferences reflect some sort of a consensus

• This idea (domain restriction) was invented before
  Arrow's theorem by Duncan Black

  • Can we solve the paradox if we restrict preference choices?

Duncan Black

• Economist (1908-1991)

• Never came to England

  • Proud Scotsman

• Social choice theorist (another founding father)

• Working on a solution for Condorcet paradox

• Invented the most famous Universal Domain restriction: Single Peakedness

The idea

• all voters are ranking the policy options on a fixed scale

  • X-axis: alternatives

  • Y-axis: ordinal rank

• We look at the shape of the preference

*Always start with the first preferences on top

What does it mean to have single-peaked preferences?

A group of agents is said to have single-peaked-preferences if:

• Each agent has an ideal choice in the set; and

• For each agent, outcomes that are further from his ideal choice are preferred less

Single-peaked preference

• All alternatives to be decided can be linearly ordered, left to right

• All voters agree on the left to right ordering; they disagree on their choices

• Everyone has a favorite point; but the favorite point differs among voters

• For each voter, as we move to the left of his/her favorite alternative, his/her utility goes down; as we move to the right of his/her favorite alternative his/her utility goes down

Single peakedness

"We will refer to a curve which is either always upward-sloping, or always downward-sloping, or which is upward-sloping to a particular point and downward-sloping beyond that point (i.e. n shaped), as being a single-peaked curve. On this definition a single-peaked curve is one which changes its direction at most once, from up to down" (Black 1958: 7)

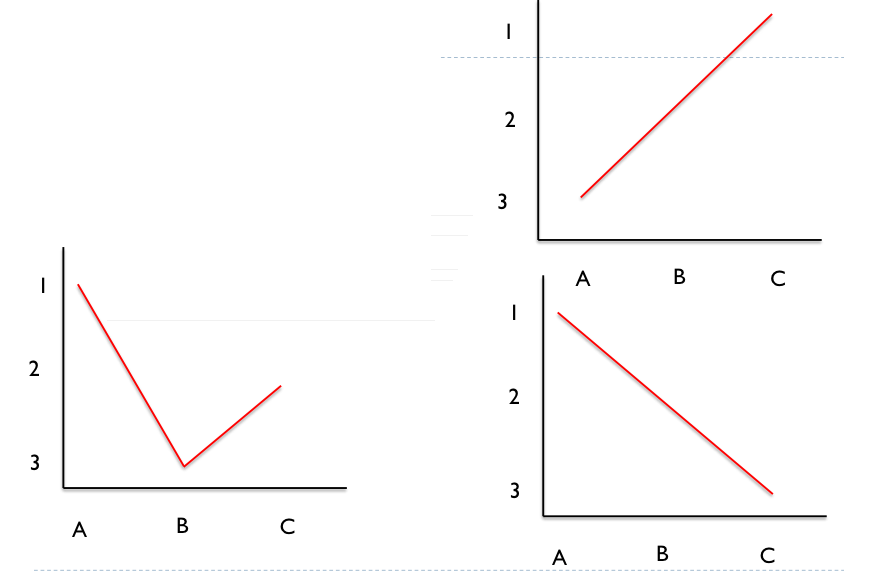
Are these individuals preference order single peaked?

Left corner: no: has two peaks (A & C)

Right top: yes: C is peak

Right bottom: yes: A is peak

Example

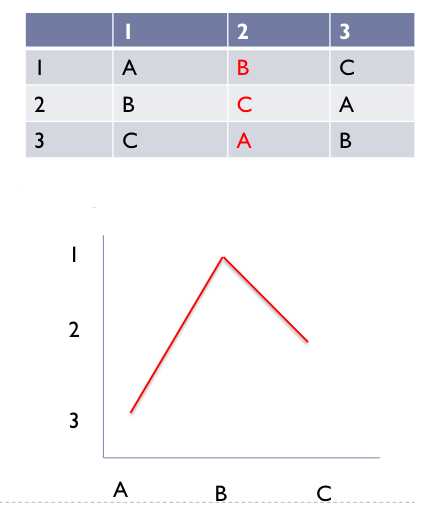
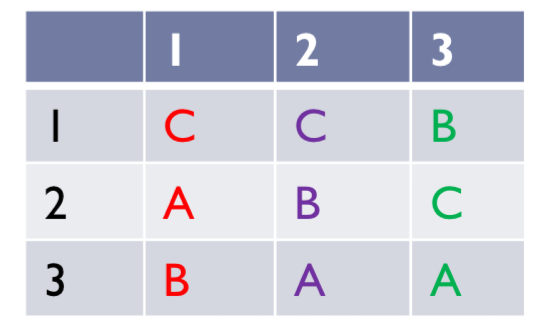
• Imagine we are in a group of 3 friends F{I, 2,3}

• Each i of F; i E F has to make a preference ordering between 3 alternatives {A, B, C}

• They have the following preference orders:

• Are they single peaked?

Condorcet winner: C

• Red: not single peaked (a c)

  • A check mark is always two peaked

• Green: single peaked (b)

• Purple: single peaked (c)

Table does not give rise to paradox

• however, maybe this is bc our way of labeling the x-axis?

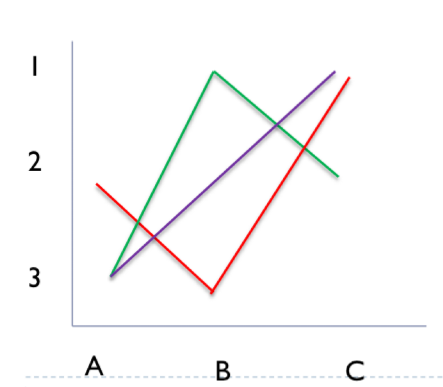
How is Condorcet paradox related to Single-peakedness?

• No matter what order the x-axis is in, if one person breaks the SP, someone will always break it if order is switched

• Condorcet cycles cannot occur when individual preferences are single-peaked

• Single-peakedness as a domain restriction, removes the occurrence of Condorcet cycles

Black’s Theorem

• If there is an odd numbers of voters that display single-peaked preferences, then a Condorcet winner exist

• In other words: by restricting condition UD, we can prove that the Condorcet paradox will never arise

• why should we assume that the voters preferences are single-peaked?

  • Deliberation

    • Negotiations → come closer to one another

Single-peakedness to median voter theorem

• If preferences are single-peaked, then majority voting on pairwise alternatives yields transitive group decisions

• Assumption: number of voters is odd (

• Assumption: we can order alternatives on I single dimension

  • Example of options that we can not order on a single dimension?

• The maximum of this ordering is the bliss point of the median voter - the voter whose bliss point has, on the common ordering, as many voters' bliss points to one side as it has to the other

  • We refer to voters' most preferred outcomes as "ideal points" or " bliss points"

  • In other words: if all voters have single-peaked curves as preferences, then the median motion will be adopted by the committee

Median example

Preferences

• papa bear: hot > warm > cold

• Mama bear: cold > warm > hot

• Baby bear: warm > hot > cold

• Each bear has one peak and one bliss-point

• Each bear likes options less and less as we move along the common ordering away from the bliss point, on either side

  • Lower utility if moving away from bliss

• In case every player has one single peak: the median option is the majority winner

• What is the majority winner? W

  • W is in the median for Mama and Papa so they are fine with it

• Who is the median voter? Baby

  • Decides

• But check all combinations of the x-axis 

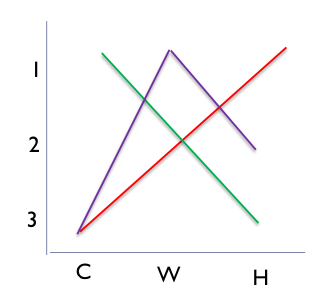
Black’s median voter theorem

when preferences are single-peaked, majority rule preferences are transitive and the feasible alternative which lies highest on the preferences of the median voter is a majority winner (a.k.a. the Condorcet winner)

• Median voter: who has the median option as their most preferred

  • This will be the option chosen

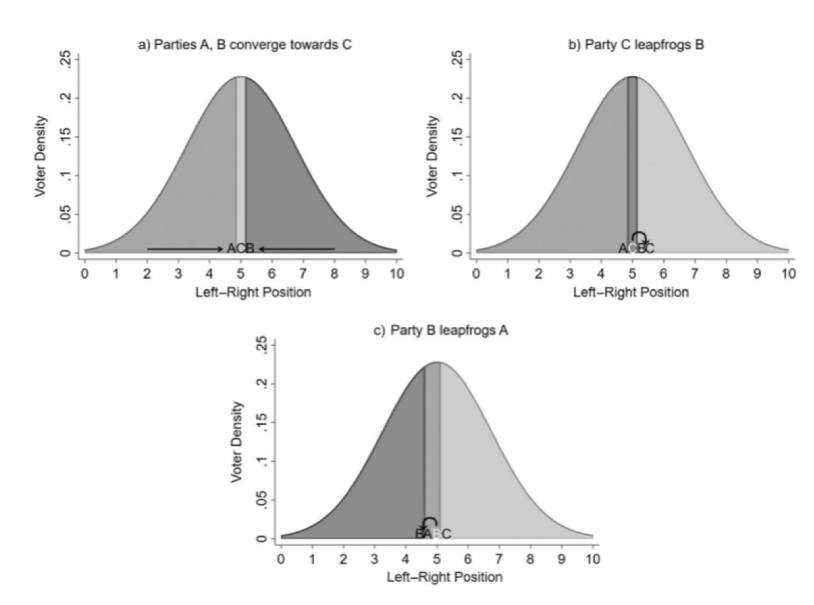
Hotelling’s model and US voting

Parties move towards the center → median

• Not seeing extreme parties in two party systems

Republican party did not do this last election

• Something not included in model: ignore ideology → does not play a role 

• So reason why median voter theory does not work in US is bc ideology was so important

Median Voter Theorem

• Black (1948) formalized this process

• If (I) we can order alternatives along a single dimension and (2) preference orderings are single-peaked along this dimension, then...

  • There is an identifiable majority preference

  • This is the preference of the median voter

  • The ideal point of the median voter has an empty winset

  • → The ideal point of the median voter cannot be defeated by a majority

  • → The ideal point of the median voter is the majority preference

Winset

• The "winset" of alternative A is the set of alternatives that can defeat A by a majority vot

  • Majority winset (Wy): is a set of alternatives that is preferred by a majority over y

• If A's winset is empty, then A cannot be defeated by another alternative

  • If so we have Condorcet winner

• In connection with Black:

  • The ideal point of the median voter has an empty winset

• In connection with Arrow:

  • It is not always the case that an empty winset exist

  • Condition U: all preferences (if complete and transitive) may be held (even cyclic ones)

  • In case of cyclic majority; the winset is not empty!

Median Voter Theorem and Politics

• This finding is very important for the proper functioning of democratic systems of government, which rest upon choices made by groups

• If preferences are organized along a single dimension, we can identify a group choice that is preferred by a majority

Median Voter Theorem: assumptions

• Full participation is assumed i.e., all members of the group have to vote

• They participate sincerely i.e., they do not misrepresent their preferences and reveal them honestly

• The median voter theory assumes that politician's lack ideological convictions, which could lead them to position themselves away from the median voter

• The median voter model assumes perfect information along three dimensions: voter knowledge of the issues; politician knowledge of the issues; and politician knowledge of voter preferences

• There is only one single dimension that plays a role...

What type of voting behavior would violate the assumptions of the MVT?

• Abstention; many voters do not vote

• Some voters vote strategically; voting for a certain candidate not bc they prefer but to avoid another candidate

• Voting on issues you are not knowledgeable in

• Clientelism

• Invalid votes

Single vs multi dimension

• The Median Voter Theorem holds for single dimension (for example, left-right dimension)

• Black shows that majority intransitivity is impossible with single-peaked preferences

• But most policies are not about a single issue

  • Rather they are packages that deal with multiple issues at the same time

    • Eg gov spending policy would include welfare spending in addition to military one

• Two theorists that deal with multidimensionality:

  • Plott

  • McKelvey

Charles Plott

• American economist (born 1938)

• Plott (1967) generalized Black's Median Voter Theorem to account for multiple dimensions

Plotts Theorem

If members of a group have circular indifference curves (i.e., possess "distance-based" spatial preferences), and if their ideal points are distributed in radially symmetric fashion around the ideal point x*, then the winset of x* is empty (i.e., x* is a Condorcet winner)

• If voters possess distance-based spatial preferences, and if their ideal points are distributed in a radially symmetric fashion with x, the ideal point of the voters, and the number of voters is odd, then x cannot be defeated in pairwise majority voting (x has an empty winset)

• We can discover multidimensional medians, and therefore a multidimensional group preference, but only under very restrictive conditions

  • Only if ideal points are distributed symmetrically around the (multidimensional) median

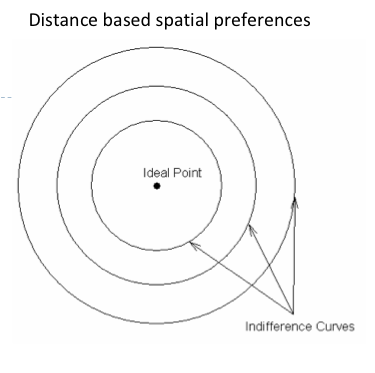
Plott Basic parameters

• These round circles are indifferent curves

  • it is a locus of policy outcomes among which an individual is indifferent (qua utility)

• The smaller the circle, the higher the utility

• The ideal point is in the middle; that is the most preferred outcome

  •  Closer to ideal point means it is closer to your preference

• If an individual's indifference curves are circular, then s/he always prefers points that are closer to those further away (i.e. s/he has
  'distance-based' spatial preferences)

• All points inside the circle, being closer to the ideal, are actually preferred by him or her to the one on the line

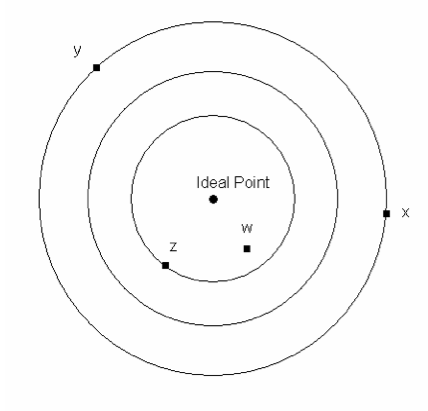
What is the preference order of these indifference curves?

W Pi Z Pi X Ii Y

Plott multiple indifference curves

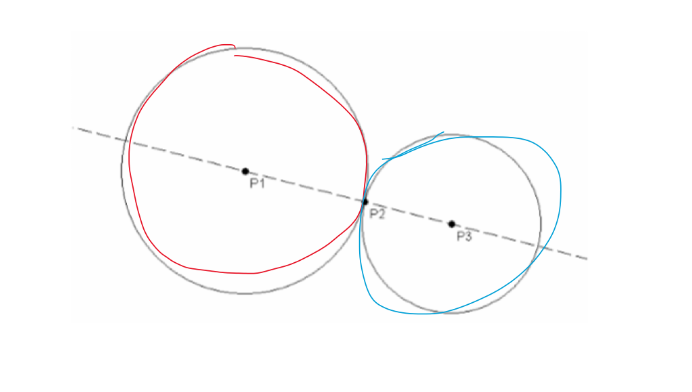
• 3 Players; 3 ideal points (pl, p2, and p3)

  • P1 indifference  curve = red

  • P3 indifference curve = blue

  • P2 circle is most likely VERY big

• Ideal point of player 2 (p2) is the median option

• Player 2 (P2) is the median voter

Plott multiple indifference curves: shifting

Imagine we shift the indifference curve and ideal point of p2

• Change to the left: p3 does not like it

• Change to the right: p1 is does not like it

P2 at its current point is stable → bliss point of p2 is very important

• Median voter

Plott: Radically symmetric fashion

the policy space is effectively one dimensional

Radically symmetric fashion explained

• The voters on each side of the median have directly opposing interest which cancel them out

• A multidimensional space becomes one-dimensional

• Answers the question: How is it distributed on the indifference curve

• The shape can be folded up into the same shape with middle staying the same → fold a round pierce of paper into triangles

Plott: multiple individuals

Imagine we have two dimensions:

1. libertarian to authoritarian

2. left-wing to right-wing

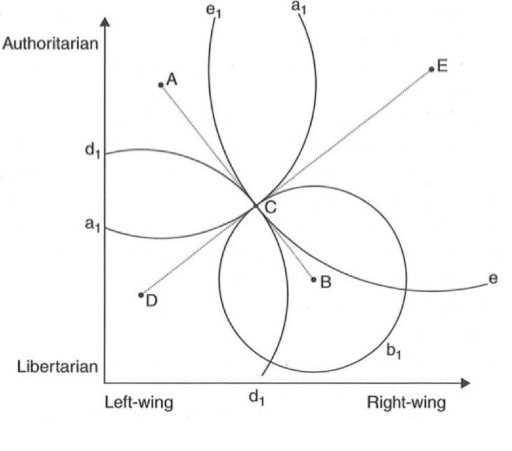
• We have 5 voters

• Each voter has an ideal point (A, B, C, D, E) and indifference curves (a1, b1, c1, d1, e1)

  • The bliss point is always in the middle of the indifference curve of that point

• Notice that voter C's ideal point is on the line between the ideal points of voters A and B as well as that between D and E

• This means that any movement away from C
  supported by A will be opposed by B, and vice versa

• No three-voter majority prefers any point to C = the majority winset of C is empty

• As in the median voter case, all others cancel each other out and the central voter is left to decide

• This is a very specific distribution of preferences!!!

  • No better bliss point that is better for everyone over C

Plott: multiple individuals shift

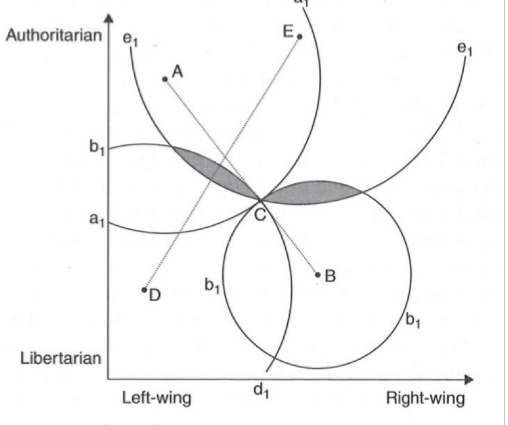
Now a voter has shifted

• Voter D and E are no longer directly opposed when it comes to movements from C

• A majority A-D-E would prefer any other point in the shaded winset

  • There is now always a majority that can win over C

• Consequently, radially symmetry no longer exists: there is no winner in a majority vote

Note: Radially symmetric does not require that the points must be equidistant from each other:"they must simply line up"

How often is Plotts theorem likely to occur?

Rarely — if ever

Anthony Downs

• (1930 - 2021)

• American economist

• Book: An Economic Theory of Voting (1957)

• Uses the Hotelling's model for his spatial model of electoral competition

• He is also known for positing the Voting Paradox

Spatial model of electoral competition: set up

• there is one ideological (economical) dimension

• Democracy

• Two parties/candidates

Spatial model of electoral competition: assumptions

• Goal for parties: Maximize political support (votes)

  • Control gov

• Goal for voters: Policy

  • As close as possible to ideal point → want ideal policy to be implemented

• Policy is unidimensional on a scale from 0 (left-wing) to 1 (right wing)

• Voters vote on party that are closest to their ideological preference

• Party who wins majority forms government

• No uncertainty in the baseline model

• Party cannot deviate from proposed policy once elected

Spatial model of electoral competition

• Based on the distribution of voters, parties and/or candidates will position themselves

  • Bell curve/normal curve

• If we fix one candidate's position first, the second candidate will be very close to this one (think about the Hotelling's model)

• Candidates should choose the position equal to the ideal point of the median voter (groups will then be of equal size)

• In other words, there is a centripetal tendency to the median voter (as was also already suggested by Black)

Spatial model of electoral competition visual

Think about the ted and ed beach video

• Converge toward the median → that is where the most voter are

• Two party system → parties will converge to the median

  • The main point of Downs 

• The starting model used to see how a lot and if voting systems work