Modeling quizzes

Quiz 1

Intro concepts, Iteration, convergence, residual, FD,TE,RO

Iteration (Loop

x₁ =1/2 (x₀+ r/x₀)

Residual

f(x_i)=ans or |f(x_i+1)|=TOL

Fixed point

Integer

Floating point

Real

Round off error

Finite accuracy which stores real numbers (storage error) Finite accuracy of arithmetic inherent error (arithmetic error)

Iterative convergence

|x₁-x₀|=ans

E_machine

smallest number you can add or subtract and still find a difference

Forward difference example

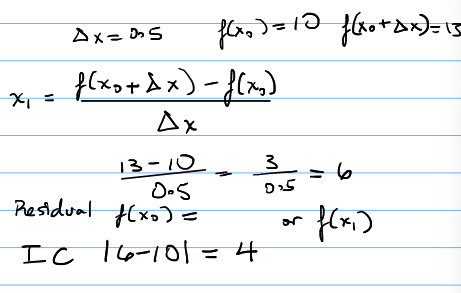
Truncation error

Due to approximations used to represent exact mathematical operations and quantities. We cant actually use an infinite number of terms.

Quiz 2

Data representation and bisection

Bisection

departs from premise that [a,b] brackets a simple root in between a and b which is p of f(x)

Bisection steps

chk midterm by p₁=a+b/2

if |f(p₁)<TOL

yes then stop; no keep going

if root is less than p₁ then [a,p]

If its greater than p₁ then [p,b]

+ then x>0, 0 then x=0, - then x<0

sign f(a)*sign(f(p₁) < 0

IEEE (Institute for electrical and electronics engineers)

Sign bit, characteristic, mantissa, bias is set by the computer when precision is declared.
c>b t is pos

c<b t is neg

t=c-b

Single Precision integer

16 bits

Largest possible integer +- 32, 767

Double Precision integer

32 bits
Largest possible integer +- 2,147,483,647

Double precision real

64 bits

Largest number is 2047 and bias is 1023

smallest number 10^-308 which is zero in double precision corresponds to zero in c and f

largest number 10³⁰⁸ corresponds to 1 in c and f

any attempt to make any smaller than +-10^-308 it just resets to that and its not fatal (real underflow error)

any attempt to make any larger than +- 10³⁰⁸ it is a fatal error (real overflow error) NAN

Single precision real

32 bits
Largest number is 255 and bias is 127

smallest number corresponds to zero +-10^-38

largest number corresponds to one +-10³⁸

any attempt to make any smaller than +-10^-38 it just resets to that and its not fatal (real underflow error)

any attempt to make any larger than +- 10³⁸ it is a fatal error (real overflow error) NAN

ex

x=-39.9
(-39.9)₁₀=-1.00111111100110011×2⁵

b=127

t=c-b

c=t+b

=5+127

=132

(132)₁₀=(10000100)₂

Putting in binary

1 is odd and 0 is even

For just a number like 25 just divide by 2 till you get to 1

and for a decimal like 0.2 just multiply by 2 till you get to the amount needed (most likely given in the question)

Ex

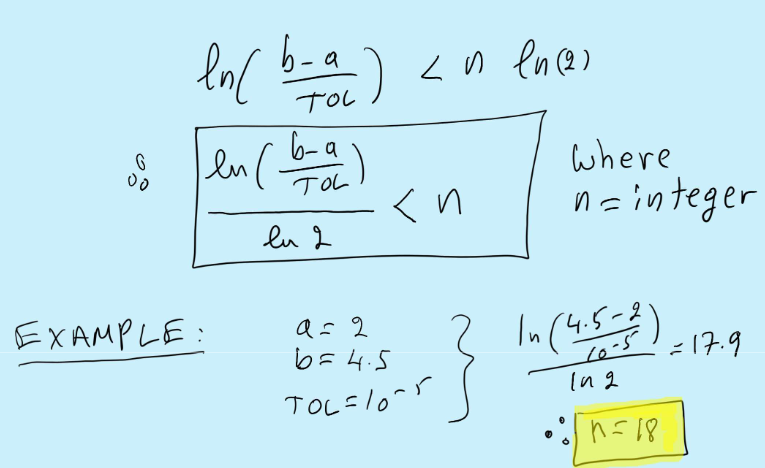
Error abs and relative

Horner’s Method

It can be used for both 1st and 2nd derivatives, It’s used to reduce round off error, and it can be applied to polynomials with complex arguments.

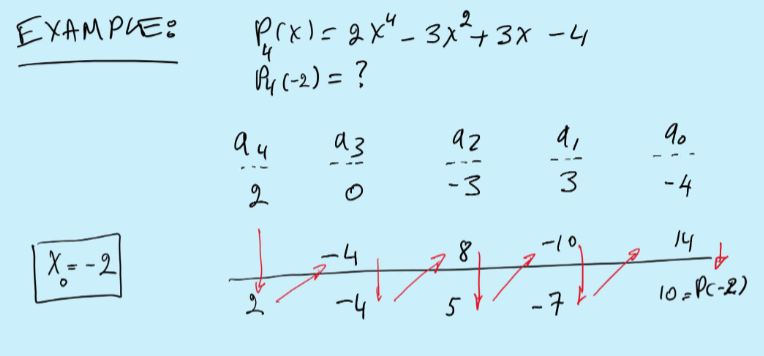
Quiz 3

fixed point, Newton-Raphson,Gauss elimination

Fixed point

Used for iterative solution of linear system of equations to solve f(x)=0 and then rearrange somehow in the form of x=g(x)

You’ll start with an initial guess then iterate

x₁= g(x₀)

x₂= g(x₁)

x₃= g(x₂)

…

x_n+1=g(x_n)

ex

You can rearrange it other ways too

To find when fixed point iteration converges

You need to use intermediate value theorem for derivatives.

Fixed Point Theorem

A sufficient but not necessary condition for the fixed point iteration. Provides a convergence criteria basically.
x=g(x)

to converge is that

|g’(x_n)|<1 for n=0,1,2,…

We can use it to check the initial guess

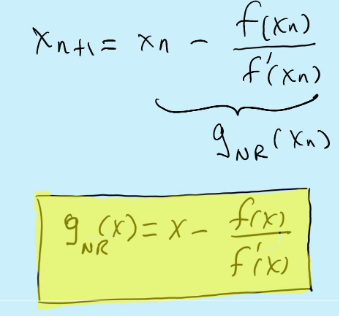
Newton-Raphson

Method requires: f(x) and f’(x)

converges “very fast” when it converges

diverges “very fast” when it diverges

a general way to find a fixed point form for any f(x) or geometrically

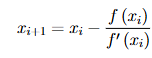
NR example

Only one initial guess

Do residual, do the 1st update

Then the residual of that |f₁(x₂)|=ans, then iterative convergence |x₂-x₁|=ans

Geometric interpretations

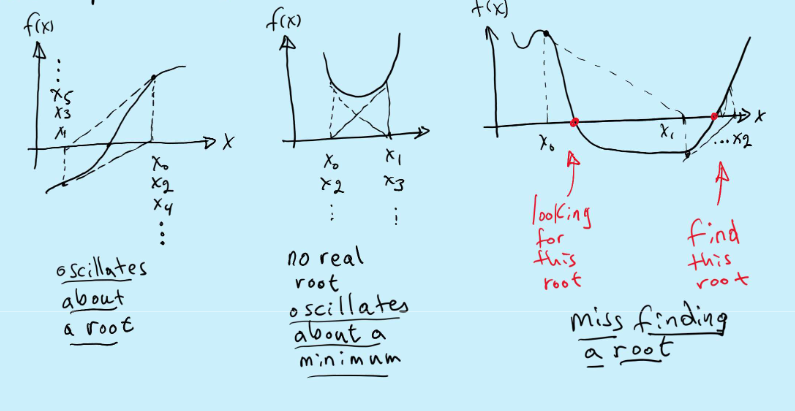
Secant Method

Approximates f’(x_n) in the NR by a backward finite difference generate iteration.

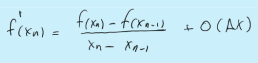
Secant Method ex

Needs two initial guesses, do residuals for both guesses, then do the 1st update, residual from that answer then the iterative convergence.

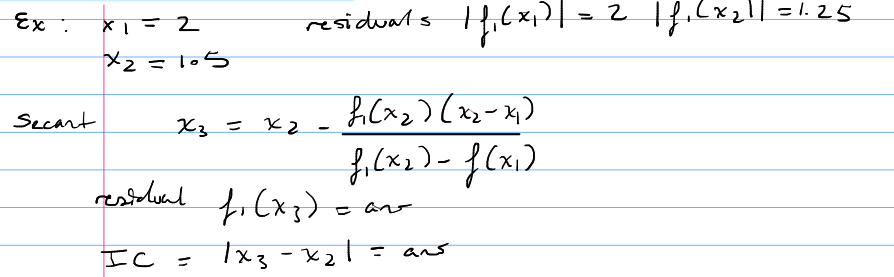
Muller’s method

Extension of secant method

Good method for complex roots

Rate of convergence is K=1.84

Requires 3 initial guesses
Assume a quadratic and use this formula to find x₃ and solve the quadratic

To avoid RO error if b²»4ac express result in an alt manner
Chk residual, update solution and we use them to find x₄ and etc

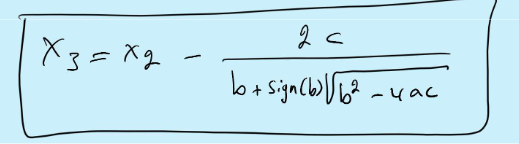
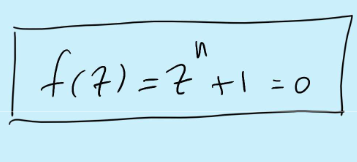
Finding roots of

initial guess

count the number of iterations to convergence

replace the location of the initial guess with the number of iterations

plot the result

Ex of the roots

End of 1st exam material

yippee

Small system of equations

N < 2,000

Use direct methods and N is limited by R.O

Large system of equations

N > 2,000
Use iterative methods. No limits on N

Gauss elimination

Its how we solve Ax=b

rearrange exactly using ERO’s Ax=b into an upper triangular form where we can find easily

det(A)

solution of Ax=b

FVM and FEM

Finite Volume Methods and Finite Element Methods

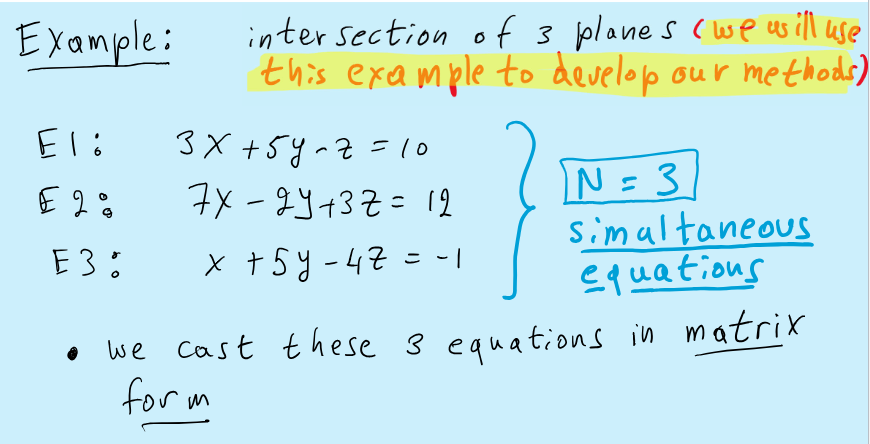
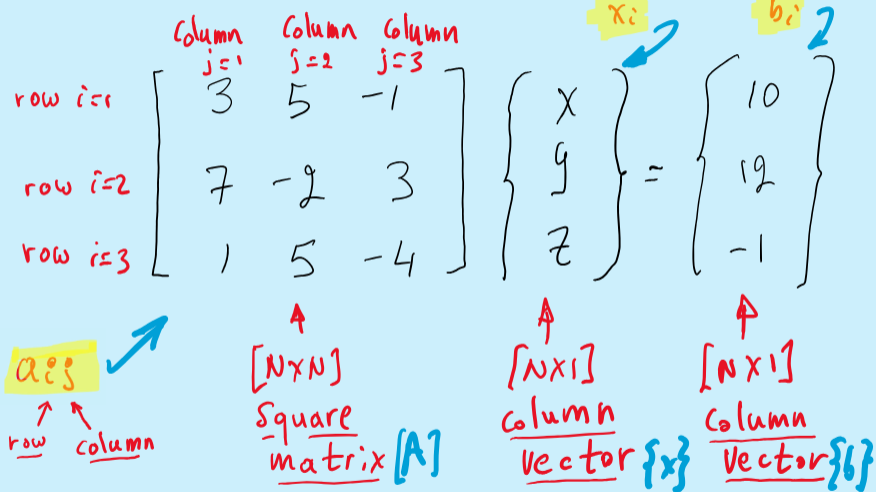
We write the equations as Ax=b

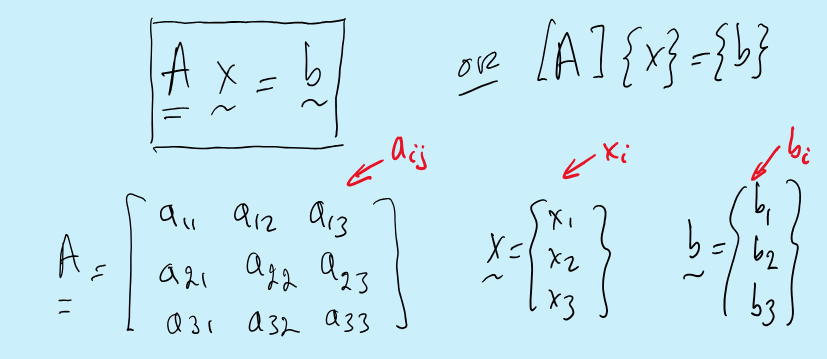
Vector norms and properties

Measures of size of vectors

||x||

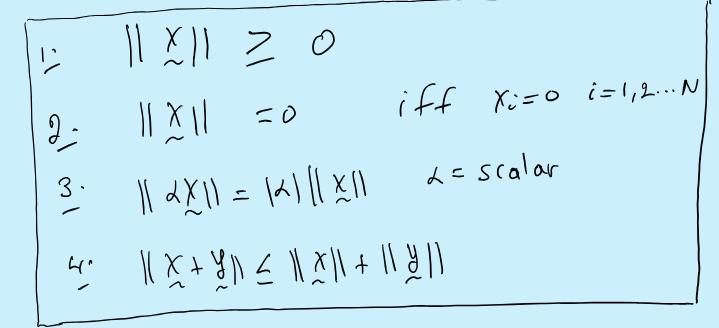
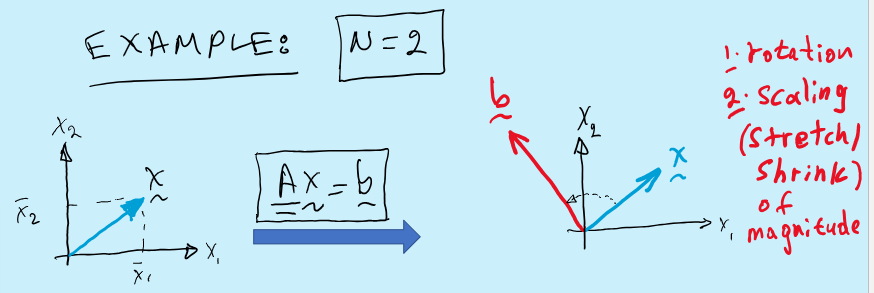
a[NxN] matrix operates on an [Nx1] vector and produces another [Nx1] vector

a linear transformation

To be able to solve a₁ and a₂ must be linearly independent

Matrix Operations

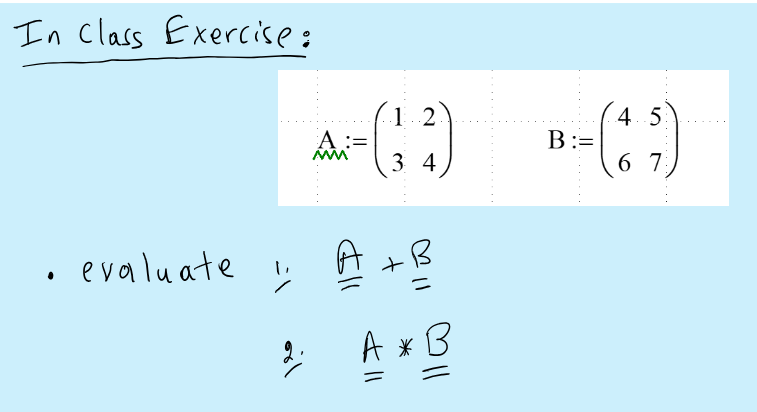
Example

Transpose

Example

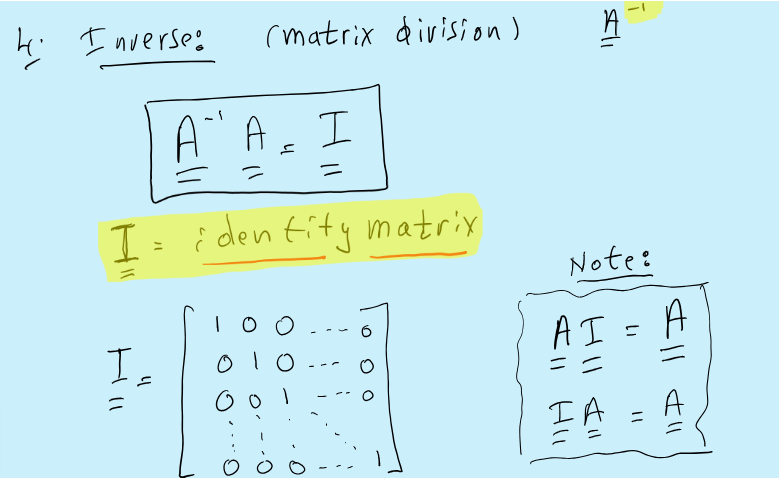
Inverse

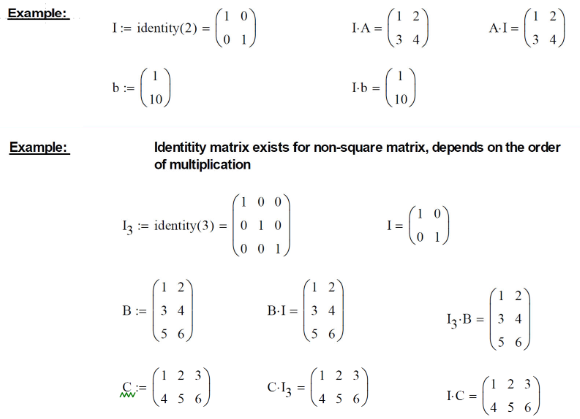
Extra example

Useful Property

(AB)^-1= B^-1A^-1

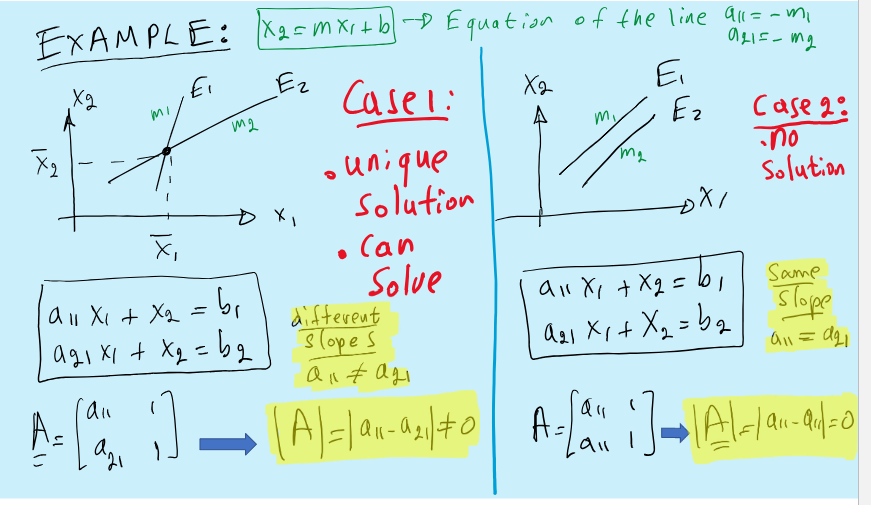
Can you always solve Ax=b

No, you can only solve if A^-1 exists and this is assured if the determinant is not zero

|A|≠0 or det(A)≠0

Determinant refresher

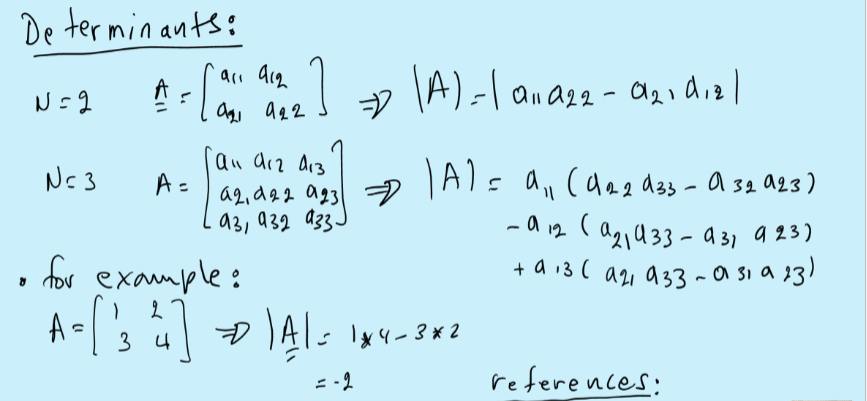
Ex:

Cramer’s Rule

Legit take the det(A)
For larger N, Cramer’s rule isnt practical it takes N! floating point operations

Ex using cramer’s rule

ERO’s

Used to rearrange in a form where the determinant can be calculated

1. multiply row by non-zero constant (scaling which scales determinant)

2. add multiple of one row to another row (rotation about root)

3. switch two rows (reorder the way equations are written change the sign of the determinant by -1)

Quiz 4

Pivoting, LU, Jacobi, Gauss Seidel, Iterative methods

The following matrix
| 0.2 -3 2 |
| 1 10 7 |
| 2 1 -8 |

will require pivoting when solved by Gauss Elimination

is not diagonally dominant

Faced with the following coefficient matrix of a system of equations to be solved by Gauss elimination methods

| -15 2 1 |
| -5 -12 1 |
| -5 7 -19|

will partial pivoting be required?

No, because the matrix is diagonally dominant

When factoring the NxN matrix [A] into its upper and lower [LU] factors

Crouts method set up the diagonal elements of [u] equal to one

Doolittle's method set the diagonal elements of [L] equal to one

Is exact except for round off error

The Thomas Algorithm

Can store and solve the problem on 4 vectors

Is used to solve tridiagonal systems of linear equations

Uses Crout's method to find the factors of the coefficient matrix [A]

The LU decomposition method applied to the linear systems [A][x] = [b] is assume that the matrix [A] is fully populated

Is used when the coefficient matrix [A] stays constant and there are multiple right hand sides [b] to solve

is a direct method of solution

is a method that takes O(N^3) floating point operations to solve the system of equations for the first right hand side vector [b] and subsequently takes O(N^2) for any new right hand side vector [b]

If a set of simultaneous equations [A][x] = [b] is solved by an iterative and [A] is 400x400 matrix and if it takes k = 10 iterations to coverage, then number of floating point operations to find of

1,600,000

If a set of simultaneous equations [A][x] = [b] is solved by an iterative and [A] is 200x200 matrix and if it takes k = 10 iterations to coverage, then number of floating point operations to find of

400,000

Iterative methods of solution for simultaneous equations include

Gauss - Seidel Iteration

Successive over relaxation (SOR)

Jacobi iteration

The system of equations
| 4 1 | {x1} = { 1 }
| 0 3 | {x2} = {5}

is solved by the Jacobi iteration and the solution vector after the 3rd iteration is

{x1}^2 = {1}
{x2} {1}

The residual norm is evaluated using the Linf norm as

4

When solving a linear system of equations by Jacobi iteration, given the following two vectors at iterations 2 and 3

{x}^2 = {0.27}
{ 0.1 }
{x}^3 = { 0.1 }
{ 0.2 }

Using the Linf norm the iterative convergence criterion is

0.17

The system of equations
| 4 1 | {x1} = { 1 }
| 0 3 | {x2} = {5}

is solved by the Jacobi iteration and the solution vector after the 3rd iteration is

{x1}^2 = {2}
{x2} {2}

The residual norm is evaluated using the Linf norm as

9

Gauss Elimination

The process of using row operations to transform a linear system into on whose augmented matrix is in row echelon form.

Quiz 5

Faced with the following coefficient matrix of a system of equations to be solved by iterative methods

| -5 2 1 |
| -5 -12 14 |
| -5 7 -19 |

Do you have any guarantee that you will obtain a solution?

No, because the matrix is not diagonally dominant

The eigenvalues of a matrix are

ya = { 1.2 }
{ -1.56}

Then when [A] pre-multiplies any vector that is not an eigenvector of [A] then it will

Decrease its magnitude
Rotate the vector

The eigenvector [A] of the matrix [A] of the linear system of equations [A][x] = [b] satisfy the following equation
Note: Here (I) is the identity matrix. [A]^T is the transpose of [A] and y is a scalar value.

[A][/\] = y[/\]

If the conditioning number of the coefficient matrix [A] of a system of linear equations [A][x] = [b] is very high

SVD can be used to solve the problem approximately by discarding the nearly linearly dependent equations

There is a large uncertainty in the error and small residuals do not necessarily indicate an accurate solution

Numerical solutions are highly sensitive to input errors

The Linf norm (row sum norm) of the following matrix

| 2 -3 2|
| 1 -1 7|
| 2 1 2|

is evaluated as

9

With respect to the eigenvalues and eigenvectors of a matrix

Eigenvalues solve an Nth order polynomial for an NxN matrix

Eigenvalues are uniquely defined and are specifically associated with that matrix

Eigenvectors are not uniquely defined and are expressed equivalently up to an arbitrary multiple of each vector

The L1 norm (column sum norm) of the following matrix is evaluated as

| -21 -3 2|
| 1 -1 7|
| 2 1 2|

24

The eigenvalues of a matrix are

ya = { 0.2 }
{ 0.56}

Then when [A] pre-multiplies any vector that is an eigenvector of [A] then it will

Decrease the magnitude
Not rotate that vector

The matrix [A] that has a norm of ||A|| = 3.2x10^3 and the norm of the inverse of the matrix is ||A^-1|| = 2.5x10^12. If a solution is obtained for a system of equations [A][x] = [b] using this same matrix and double precision computations then

The solution is very sensitive to input error.

Small residuals do not indicate accurate answers.

The system is ill-conditioned.

Quiz 6

When applied to solving the system of non-linear equations
f(x) = 0
one step equivalent of the Newton Raphson method is

{x}^n+1 = {x}^n - [J({x}^n)]^-1 {f({x}^n}

When solving the simultaneous set of coupled non-linear equations {f(x)} = 0 by the Newton Raphson iterative method, the iteration is stopped when the residual criterion is met.

If the n+1th solution vector is {x}^n+1, then the residual stopping criterion is defined in terms of some appropriate vector norm || || and a user-supplied error tolerance TOL as:

|| f{x}^n+1 || < TOL

The Levenberg Marquardt algorithm

is a method that automatically combines steepest descent and the Newton Raphson algorithm for solving non-linear equations

The Jacobian Matrix [J] that arises in the Newton Raphson method for simultaneous non-linear equations {f(x)} = 0

Has entries Jij = parfi/ parxj
Must be updated at each iteration

Given the two simultaneous non-linear equations to be solved by the Newton-Raphson method

f1(x) = x1 - 2x1x2
f2(x) = 6x1-x1^3x2

and a current solution vector at the n+1 iteration
(x1)^n+1 = (2)
(x2) (2)
then the element J2,2 of the Jacobian matrix is evaluated as

-8

The Jacobian matrix evaluates for N = 10 simultaneous non-linear equations

has 100 entries of partial derivatives

can be approximately evaluated using finite differences

Given the two simultaneous non-linear equations to be solved by the Newton-Raphson method

f1(x) = x1 - 2x1x2
f2(x) = 6x1-x1^3x2

and a current solution vector at the n+1 iteration
(x1)^n+1 = (2)
(x2) (2)
then the element J1,2 of the Jacobian matrix is evaluated as

-4

When solving the simultaneous set of coupled non-linear equations {f(x)} = 0 by the Newton Raphson iterative method, the iteration is stopped when the residual criterion is met.

If the n-th solution vector is {x}^n+1, then the residual stopping criterion is defined in terms of some appropriate vector norm || || and a user-supplied error tolerance TOL as:

|| {x}^n+1 - {x}^n || < TOL