Moving charges and magnetism

Oersted experiment

accidentally discovered that whenever current carrying conductor is present in a particular area it will produce some magnetic field around it

Biot Savarts law

Magnetic field at the centre of circular current loop

Magnetic field at the axis of circular current loop

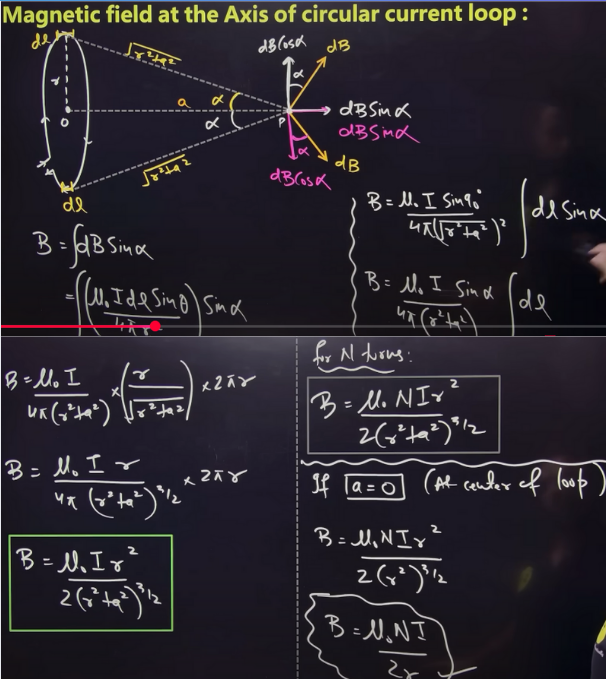
rule for finding directon of magnetic field due to circular current loop

• right hand thumb rule

• clock rule

Ampere’s circuital law and its PROOF

the line intergral of the magnetic field surrounding closed loop equals to the number of times the algebraic sum of currents passing through the loop producted with nu not

THE LINE INTEGRAL OF MAGNETIC FIELD FOR CLOSED LOOP IS NUENOT TIMES THE NET CURRENT THREADENING THE SURFACE

application of ampere circuital law to a straight conductor

• formula for circular loop and straight conductor is almost same so try remembering

magnetic field of a straight solenoid (inside)

let us take a solenoid of length ‘l’ and area of cross section ‘A’ if ‘n’ is the number of turns per unit length and taking rectangular amperes loop abcd as shown then:

(The magnetic field outside a long, straight solenoid is considered to be zero)

motion of a charged particle in a unform magnetic field

moving charged particle ll to magnetic field

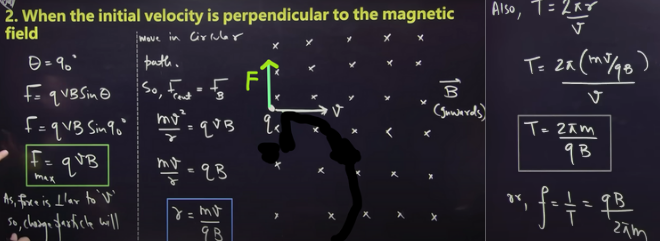
moving charged particle perpendicular to magnetic field

Magnetic field can change direction of velocity of charge but not magnitude of velocity of charge

KE= constant

KE of a charge can only be change by electric field not magnetic field

(whenever a charged particle enters a uniform magnetic field, time period remains constant / time period is independant of velocity)

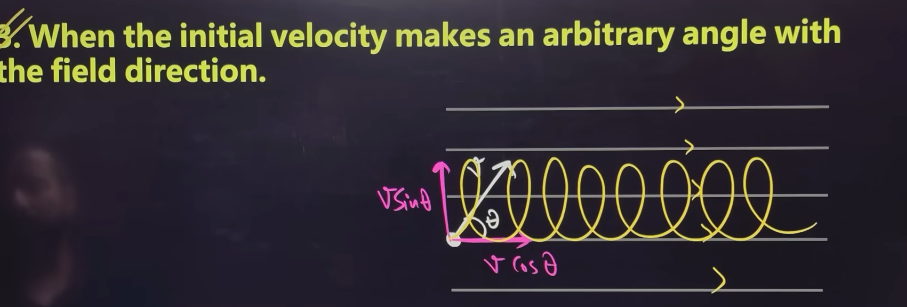
moving charged particle makes an arbitrary angle to magnetic field

as velocity is making angle theta in a uniform magnetic field the cos theta component will tend to move the charged particle in forward direction and sin theta component which is perpendicular to magnetic field will tend to move the charged particle in circular motion. hence due to both the components the charged particle will move in helical path forward in direction

show that KE remains constant for charged particles

Force expression for a straight current carrying wire

F= ILBSintheta

let us take a conductor of length ‘l’ area of cross section ‘A’ carrying a current ‘I’ in uniform magnetic field B making angle theta with the wire. if ‘n’ is number of electrons per unit vol then:

derieve an expression for force per unit length between two infinite long straight parallel current carrying wires, hence definition of 1 Ampere

Let us consider 2 parallel wires carrying current I₁ and I₂ in the same direction having ‘d’ distance inbetween the wires then:

(same direction- attract

opp direction- repel)

def for 1 ampere

Torque experienced by a current carrying loop in unform magnetic field

Moving coil galvanometer

Principle:

whenever a current carrying conductor is kept in magnetic field it experiences a force and current carrying loop in magnetic field experiences torque